湖北省武汉市洪山区2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. “翻开人教版《数学》九年级下册课本恰好翻到第56页”这个事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、无法确定

查看试题解析
2. “致中和，天地位焉，万物育焉”．对称美是我国古人和谐平衡思想的体现，常被运用于建筑，器物，绘画，标识等作品的设计上，使对称之美惊艳了千年．下列大学校徽的主体图案是中心对称图形的是（）

A、北京体育大学 B、华中师范大学 C、清华大学 D、武汉大学

查看试题解析
3. 如图，若 $⊙ O$ 的半径为4，圆心O到某条直线的距离为3，则这条直线可能是（）

A、 $l_{1}$ B、 $l_{2}$ C、 $l_{3}$ D、 $l_{4}$

查看试题解析
4. 把方程 $x^{2} - 6 x + 3 = 0$ 化为 ${(x + m)}^{2} = n$ 的形式，则 $m + n$ 的值是（）

A、7 B、3 C、5 D、 $- 3$

查看试题解析
5. 将二次函数 $y = - 2 x^{2} - 4 x + 1$ 的图象如何移动才能得到 $y = - 2 x^{2}$ 的图象（）

A、向左移动1个单位，向上移动3个单位 B、向右移动1个单位，向上移动3个单位 C、向左移动1个单位，向下移动3个单位 D、向右移动1个单位，向下移动3个单位

查看试题解析
6. 有一个人患了流感，经过两轮传染后，共有36人患了流感，设每轮传染中平均一个人传染了x个人，则下列结论错误的是（）

A、1轮后有 $(x + 1)$ 个人患了流感 B、第2轮又增加 $x (x + 1)$ 个人患流感 C、依题意可以列方程 ${(x + 1)}^{2} = 36$ D、按照这样的传播速度，三轮后一共会有180人感染

查看试题解析
7. 若一元二次方程 $x^{2} - 4 x - 3 = 0$ 的两个不相等的实数根为 $x_{1} ， x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值是（）

A、 $- \frac{3}{4}$ B、 $\frac{3}{4}$ C、 $- \frac{4}{3}$ D、 $\frac{4}{3}$

查看试题解析
8. 已知一个圆心角为 $240 °$ ，半径为3的扇形工件，没搬动前如图所示（A，B两点触地放置），向右滚动工件至点B再次触地时停止，则圆心O所经过的路线长是（）

A、6 B、 $3 π$ C、 $6 π$ D、 $12 π$

查看试题解析
9. 如图，点C，点D，点E分别是以AB，AC，BC为直径的半圆弧的一个三等分点，再分别以AD，DC，CE，BE为直径向外侧作4个半圆，若图中阴影部分的面积为 $\sqrt{3}$ ，则AB的长为（）

A、 $2 \sqrt{2}$ B、2 C、4 D、 $2 \sqrt{3}$

查看试题解析
10. 抛物线 $y = m x^{2} + 4 m x - 4$ 上有 $(1 ， y_{1})$ ， $(2 ， y_{2})$ ， $(- 2 + \sqrt{3} ， y_{3})$ ， $(- 2 - \sqrt{3} ， y_{4})$ 四点，若 $y_{1} ， y_{2} ， y_{3} ， y_{4}$ 四个数中有且只有一个大于零，则m的取值范围为（）

A、 $m \leq \frac{1}{3}$ B、 $m < \frac{4}{5}$ C、 $\frac{1}{3} \leq m < \frac{4}{5}$ D、 $\frac{1}{3} < m \leq \frac{4}{5}$

查看试题解析

二、填空题

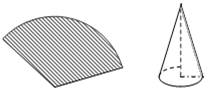
11. 在平面直角坐标系中，点 $P (3 ， - 4)$ 关于原点对称的点的坐标是．

查看试题解析
12. 为了估计鱼塘中鱼的数量，养鱼者首先从鱼塘中打捞100条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘，一段时间后再从鱼塘中打捞 50 条鱼.如果在这些鱼中有10条鱼是有记号的，那么估计鱼塘中鱼的条数为．

查看试题解析
13. 1275年，我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题：“直田积八百六十四步，只云阔不及长一十二步，问阔及长各几步．”意思是：矩形面积864平方步，宽比长少12步，问宽和长各几步．其中长为步．

查看试题解析
14. 如图，用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽，则这个纸帽的高是cm ．

查看试题解析
15. 已知二次函数 $y = a x^{2} + 2 a x + c$ （a，c为常数且 $a < 0$ ）经过 $(1 ， m)$ ，且 $m c < 0$ ，下列结论：① $c > 0$ ；② $a < - \frac{c}{3}$ ；③若关于x的方程 $a x^{2} + 2 a x = p - c (p > 0)$ 有整数解，则符合条件的p的值有2个；④当 $a \leq x \leq a + 3$ 时，二次函数的最大值为c，则 $a = - 4$ .
其中一定正确的有.（填序号即可）

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 30 °$ ，过A，C两点的 $⊙ O$ 交线段 $A B$ 于D点， $A E ∥ B C$ 交 $⊙ O$ 于E点， $D E$ 交 $A C$ 于F，则 $\frac{A F}{F C}$ 的最大值为.

查看试题解析

三、解答题

17. 已知关于x的一元二次方程 $x^{2} - (m + 1) x + m + 6 = 0$ 的其中一个根为3．求m的值及方程的另一个根．

查看试题解析
18. 如图，点E是正方形 $A B C D$ 内一点，连接 $A E ， B E ， C E$ ，将 $△ A B E$ 绕点B顺时针旋转90°到 $△ C B E^{'}$ 的位置（ $△ A B E ≌ △ C B E^{'}$ ），连接 $E E^{'}$ ．

(1)、判断 $△ B E E^{'}$ 的形状为；

(2)、若 $A E = 2$ ， $B E = 4$ ， $C E = 6$ ，求 $∠ B E^{'} C$ 的度数．

查看试题解析
19. 某班数学兴趣小组进行如下活动：组长从一副扑克牌中选取六张分给两位同学，小明分到的三张扑克牌分别是方块 $6$ ， $8$ ， $10$ ；小亮分到的是方块 $5$ ， $7$ ， $9$ ．两人将分到的牌随机放在桌上（数字一面朝下），然后各自从对方的牌中抽一张进行比较，抽牌数字较大的人当“小老师”，给全班同学讲一个关于数学家的故事．

(1)、若小亮从对方的扑克牌中抽一张，则抽到方块 $10$ 的概率是；

(2)、用列表法或画树状图法中的一种方法，求小明能当“小老师”的概率．

查看试题解析
20. 菱形 $A B C D$ 的顶点B，C，D在 $⊙ O$ 上，O在线段 $A C$ 上.
图1 图2

(1)、如图1，若 $A B$ 是 $⊙ O$ 的切线，求 $∠ A D C$ 的大小；

(2)、如图2，若 $A B = 2 \sqrt{6}$ ， $A C = 8$ ， $A B$ 与 $⊙ O$ 交于点E，求 $B E$ 的长.

查看试题解析
21. 如图，在 $12 \times 9$ 正方形网格中，每个小正方形的顶点称为格点.B，C为格点，以线段 $B C$ 为直径的 $⊙ O$ 交纵向格线于A点，连接 $A B ， A C$ .仅用无刻度的直尺在给定网格中按要求作图，画图过程用虚线表示，画图结果用实线表示.

(1)、在图1中作出圆心O；

(2)、在图1中作 $A D$ 平分 $∠ B A C$ 交 $⊙ O$ 于D点：

(3)、在图1中作 $A B$ 绕D点顺时针旋转 $90 °$ 后的线段；

(4)、在图2的 $⊙ O$ 中作弦 $A M = A B$ .

查看试题解析
22. 在投掷实心球的运动中，实心球出手时水平向前的速度为a（单位： $m / s$ ），垂直向上的速度为b（单位： $m / s$ ），实心球在空中运动时，其水平距离x（单位：m）与时间t的关系为 $x = a t$ ，高度y（单位：m）与时间t的关系为 $y = - 5 t^{2} + b t + 2$ ．

(1)、在小伟同学的一次投掷中，测得 $a = 6 m / s$ ， $b = 3 m / s$ ；
①写出x与t的函数关系式为 ▲ ；y与t的函数关系式为 ▲ ；
根据以上关系，可得y与x的函数关系式为 ▲ （不用写出x的取值范围）；
②求出本次实心球的投掷距离．

(2)、研究表明：在投掷力度一定时，水平速度与垂直向上的速度越接近，则实心球的投掷距离越远，改进投掷方法后，小伟投出了 $8 m$ 的最佳成绩，若本次投掷中 $a = b$ ，求实心球在投掷过程中的最大高度．

查看试题解析
23. 在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， D为平面内一点.
图1 图2

(1)、当D在线段 $B C$ 上时，将线段 $A D$ 绕点A顺时针旋转 $90 °$ 至 $A E$ ，连接 $B E$ ，请你在图1中完成作图，并直接写出 $B E$ 和 $B C$ 的位置关系 ▲ ；

(2)、在（1）的条件下，连接 $E D$ 交 $A B$ 于G，过点C作 $A C$ 的垂线交 $E D$ 延长线于点F，试判断线段 $F G$ 与 $A D$ 的数量关系并证明；

(3)、如图2，点D位于 $△ A B C$ 上方，且 $∠ A D C = 45 °$ ， $△ B D C$ 的面积为9，直接写出 $C D$ 的长度.

查看试题解析
24. 已知直线 $l ： y = k x + b (k > 0)$ 与抛物线 $C ： y = a x^{2} (a > 0)$ 有唯一公共点 $P$ ，直线 $l$ 分别交 $x$ 轴， $y$ 轴于 $A ， B$ 两点．
图1 图2 图3

(1)、如图1，当 $a = 1$ ， $k = 1$ 时，求 $b$ 的值；

(2)、如图2，当 $a = \frac{1}{2}$ 时，过点 $A$ 作直线 $l$ 的垂线交 $y$ 轴于点 $T$ ，求 $T$ 坐标；

(3)、如图3，当 $k = 1$ 时，平移直线 $l$ ，使之与抛物线 $C$ 交于 $M ， N$ 两点，点 $P$ 关于 $y$ 轴的对称点为 $Q$ ，求证： $∠ M Q P = ∠ N Q P$ ．

查看试题解析