2024年人教版中考数学二轮复习 专题2 整式与因式分解
试卷更新日期:2024-02-23 类型:二轮复习
一、选择题
-
1. 单项式 的系数和次数分别是( )A、 ,6 B、 ,5 C、 ,5 D、 ,52. 已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )A、8.23×10﹣6 B、8.23×10﹣7 C、8.23×106 D、8.23×1073. 下列说法正确的是( )A、 是六次多项式 B、 是单项式 C、 的系数是 ,次数是2次 D、 +1是多项式4. 如图一标志性建筑的底面呈正方形,底面采用块完全相同的长方形地砖和一块正方形地砖拼成,则以下说法正确的是( )
 A、由里面小正方形地砖的周长可求长方形的面积 B、由里面小正方形地砖的面积可求大正方形的面积 C、由长方形地砖的面积可求外面大正方形的面积 D、由长方形地砖的周长可求外面大正方形的面积5. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、16. 当x=l时,代数式ax3-3bx+5的值是2019,则当x=-l时,这个代数式的值是( )A、2014 B、-2019 C、2009 D、-20097. 如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
A、由里面小正方形地砖的周长可求长方形的面积 B、由里面小正方形地砖的面积可求大正方形的面积 C、由长方形地砖的面积可求外面大正方形的面积 D、由长方形地砖的周长可求外面大正方形的面积5. 若x+m与2﹣x的乘积中不含x的一次项,则实数m的值为( )A、﹣2 B、2 C、0 D、16. 当x=l时,代数式ax3-3bx+5的值是2019,则当x=-l时,这个代数式的值是( )A、2014 B、-2019 C、2009 D、-20097. 如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( ) A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、a2+ab=a(a+b)8. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有18颗棋子,…,则第⑥个图形中棋子的颗数为( )
A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、a2+ab=a(a+b)8. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有18颗棋子,…,则第⑥个图形中棋子的颗数为( ) A、45 B、63 C、84 D、1089. 若实数a,b,c满足条件则a,b,c中 ( )A、必有两个数相等 B、必有两个数互为相反数 C、必有两个数互为倒数 D、每两个数都不相等10. 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第2023拍时,你听到的是( )
A、45 B、63 C、84 D、1089. 若实数a,b,c满足条件则a,b,c中 ( )A、必有两个数相等 B、必有两个数互为相反数 C、必有两个数互为倒数 D、每两个数都不相等10. 如图,敲击三根管时依次发出“1”、“3”“5”,两只音锤同时从“1”开始,以相同的节拍往复敲击,不同的是:甲锤每拍移动一位(左中右中左中右…),乙锤则在两端各有一拍不移位(左中右右中左左中右…),在第2023拍时,你听到的是( ) A、同样的音“1” B、同样的音“3” C、同样的音“5” D、不同的两个音11. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )
A、同样的音“1” B、同样的音“3” C、同样的音“5” D、不同的两个音11. 如图,在长方形ABCD中,AB=6,BC=10,其内部有边长为a的正方形AEFG与边长为b的正方形HIJK,两个正方形的重合部分也为正方形,且面积为5.若右侧阴影部分的面积S2是左侧阴影部分面积S1的4倍,则正方形AEFG与正方形HIJK的面积之和为( )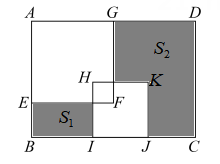 A、20 B、25 C、 D、
A、20 B、25 C、 D、二、填空题
-
12. 因式分解:.13. 已知 ,则代数式 的值为.14. 对于三个互不相等的有理数 , , , 我们规定符号表示 , , 三个数中较大的数,例如按照这个规定则方程的解为 .15. 某种商品的原价每件a元,第一次降价打“八折”,第二次降价又减10元.则两次降价后的售价为 元.16. 对于有理数x,y,定义一种新运算:x⊕y=ax+by-5,其中a,b为常数.已知1 ⊕2=9,(-3)⊕3=-2,则2a+b=.17. 对于两个不相等的实数a、b , 我们规定符号表示a , b中的较小的值,如 , 按照这个规定,方程的解为 .18. 如图,现有边长分别为和的正方形纸片,以及长、宽分别为的长方形,其中 . 将两正方形纸片按图1和图2两种方式(图1和图2中两张正方形纸片均有部分重叠)放置于长方形中,其中未被覆盖的部分用阴影表示.若图1中阴影部分的面积记为 , 图2中阴影部分的面积记为 . 则 .
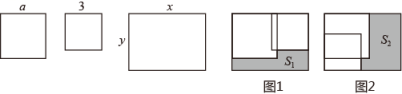 19. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37)….如果单独把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对:.
19. 如图,图中数字是从1开始按箭头方向排列的有序数阵.从3开始,把位于同一列且在拐角处的两个数字提取出来组成有序数对:(3,5);(7,10);(13,17);(21,26);(31,37)….如果单独把每个数对中的第一个或第二个数字按顺序排列起来研究,就会发现其中的规律.请写出第n个数对:.
三、计算题
-
20. 选用合适的方法将下列各式分解因式:(1)、5x2+7x-6.(2)、3a2b2-17abxy+10x2y2 .(3)、a2+2ab+ac+bc+b2(4)、a2-a2b+ab2-a+b-b2 .(5)、x2-16x-561.(6)、(x2+5x+3)(x2+5x-2)-6.21. 先化简,再求值:(1)、 , 其中 .(2)、 , 其中 , .22. 先化简再求值: 4( x2﹣3xy﹣y2)﹣3(x2﹣7xy﹣2y2),其中x,y满足(x+1)2+|y﹣2|=0.
四、解答题
-
23. 如图,用同样规格的黑白两色的正方形瓷砖铺设长方形地面,请观察下列图形并解答有关问题:
 (1)、第个图形中,第一行共有块瓷砖,第一列共有块瓷砖,该图中白色瓷砖共有块.(2)、第个图形中,铺设地面所用黑色瓷砖的块数为 . (用含的代数式表示)24. 某城市出租车的收费标准为:行驶里程不超过收费元,超过的部分按每千米加元收费小丽乘出租车从体育馆到少年宫.(1)、若行驶里程为 , 则用的代数式表示费用.(2)、如果小丽乘坐的出租车行驶了 , 小丽只有元钱,付车费够不够?25. 如图,某小区有一块长为(2a+3b)米,宽为(3a+2b)米的长方形地块,物业公司计划在小区内修一条平行四边形小路,小路的底边宽为a米,将阴影部分进行绿化.
(1)、第个图形中,第一行共有块瓷砖,第一列共有块瓷砖,该图中白色瓷砖共有块.(2)、第个图形中,铺设地面所用黑色瓷砖的块数为 . (用含的代数式表示)24. 某城市出租车的收费标准为:行驶里程不超过收费元,超过的部分按每千米加元收费小丽乘出租车从体育馆到少年宫.(1)、若行驶里程为 , 则用的代数式表示费用.(2)、如果小丽乘坐的出租车行驶了 , 小丽只有元钱,付车费够不够?25. 如图,某小区有一块长为(2a+3b)米,宽为(3a+2b)米的长方形地块,物业公司计划在小区内修一条平行四边形小路,小路的底边宽为a米,将阴影部分进行绿化. (1)、用含有a、b的式子表示绿化的总面积S(2)、若a=2,b=4,求出此时绿化的总面积S.26. 如图,在长方形中, , 点从点出发,沿折线以每秒个单位的速度向点运动,同时点从点出发,沿以每秒个单位的速度向点运动,当点到达点时,点、同时停止运动设点的运动时间为秒.
(1)、用含有a、b的式子表示绿化的总面积S(2)、若a=2,b=4,求出此时绿化的总面积S.26. 如图,在长方形中, , 点从点出发,沿折线以每秒个单位的速度向点运动,同时点从点出发,沿以每秒个单位的速度向点运动,当点到达点时,点、同时停止运动设点的运动时间为秒.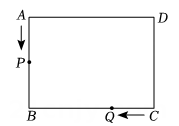 (1)、当点在边上运动时, ;当点在边上运动时, 用含的代数式表示(2)、当点与点重合时,求的值.(3)、当时,求的面积.(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.27. 某品牌童装专卖店新推出 A,B,C三种款式的春装.某个周末的销售量(单位:件)如(下表:)
(1)、当点在边上运动时, ;当点在边上运动时, 用含的代数式表示(2)、当点与点重合时,求的值.(3)、当时,求的面积.(4)、若点关于点的中心对称点为点 , 直接写出和面积相等时的值.27. 某品牌童装专卖店新推出 A,B,C三种款式的春装.某个周末的销售量(单位:件)如(下表:)A
B
C
合计
周六的销售量
y
30
周日的销售量
x
2y
4x
5x+2y
合计
10
3y
30+5x+2y
(1)、请根据表格信息,补全表格中的划线部分(用含 x,y的代数式表示).(2)、已知A 款周六的销售量与 B 款周日的销售量相等,且这个周末C款的销售总量比A,B 两款的销售总量之和还多 4件.①求x,y的值.
②已知三种款式的春装单价均为大于 100 的整数,且 A 款的单价是 B 款的 3 倍.如果周六的总销售额为 5 600元,那么B款的单价可以是 (写出所有可能的结果).
五、实践探究题
-
28. 阅读材料,解决问题:
把根式 进行化简,若能找到两个数m,n,满足 且 则可以把 变成 , 开方,从而使得 化简.
例如:化简
解:
(1)、化简:(2)、已知 1≤a≤2,化简:29. 先阅读材料,再解答问题:恒等变形是代数式求值的一个很重要的方法.利用恒等变形,可以把无理数运算转化为有理数运算,可以把次数较高的代数式转化为次数较低的代数式.
例如:当 时,求 的值.
为解答这道题,若直接把 代入所求的式子中进行计算显然很麻烦,我们可以通过恒等变形对本题进行解答:
将条件变形,由 得 再把等式两边同时平方,把无理数运算转化为有理数运算.
由 得 即 =2x+2.
原式
(1)、若 求 的值.(2)、若 求 的值.六、综合题
-
30. 如图,面积为30的长方形的边在数轴上,为原点,.线段从OC出发,以每秒1个单位的速度向右移动,与此同时线段从出发以每秒2个单位的速度向左移动.连结 , 新长方形与原长方形重叠部分的面积记为 , 设运动时间为.
 (1)、当在O、A之间,用含的代数式表示:.(2)、恰好等于原长方形面积的一半时,数轴上点表示的数是多少?(3)、长方形与长方形未重叠部分的面积记为 , 请直接写出时,的值.31. 数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数恒等式,很多都可以借助几何图形进行直观推导和解释.请结合相关知识,解答下列问题:
(1)、当在O、A之间,用含的代数式表示:.(2)、恰好等于原长方形面积的一半时,数轴上点表示的数是多少?(3)、长方形与长方形未重叠部分的面积记为 , 请直接写出时,的值.31. 数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们进行推理,获得结论.初中数学里的一些代数恒等式,很多都可以借助几何图形进行直观推导和解释.请结合相关知识,解答下列问题: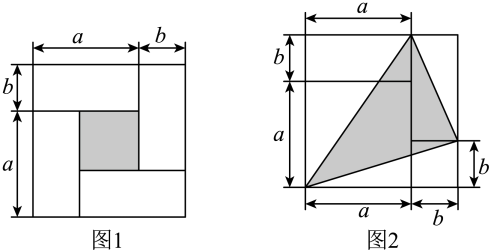 (1)、如图1是由4个大小相同,长为a、宽为b的长方形围成的边长为的正方形,用含字母a,b的代数式表示出阴影部分的面积.
(1)、如图1是由4个大小相同,长为a、宽为b的长方形围成的边长为的正方形,用含字母a,b的代数式表示出阴影部分的面积.①通过计算阴影部分正方形的边长,求阴影部分的面积,可列代数式:;
②通过用较大正方形的面积减去4个小长方形的面积,求阴影部分的面积,可列代数式:;
(2)、根据图1中的阴影部分的面积关系写出一个代数恒等式:;(3)、若 , , 求图2中阴影部分的面积.