广东省茂名市2023-2024学年高一上学期期末质量监测数学试题

试卷更新日期：2024-02-23 类型：期末考试

进入出卷网下载

一、选择题：本大题共8小题，每小题5分，共40分．每小题给出的四个选项中，只有一项是符合题目要求的。

1. $c o s 780 ° =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
2. 设集合 $A = {x | - 3 < x < 2}$ ， $B = {x | f (x) = l g (x + 1) + l g (1 - x)}$ ，则 $A ∪ B =$ （）

A、 ${x | x < 2}$ B、 ${x | - 3 < x < 2}$ C、 ${x | - 2 < x < 2}$ D、 ${x | x > - 3}$

查看试题解析
3. “ $Δ = b^{2} - 4 a c < 0$ ”是“关于x的一元二次不等式 $a x^{2} + b x + c > 0$ 的解集为R”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 方程 $l g x - 4 = - x$ 的解所在的区间为（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析
5. 已知幂函数 $f (x) = (m - 1) x^{m^{2} - 1}$ ，则 $f (- 1) =$ （）

A、 $- 1$ B、1 C、 $- 2$ D、2

查看试题解析
6. 已知 $a = e^{0.8}$ ， $b = 0 . 8^{e}$ ， $c = l o g_{\frac{1}{2}} e$ ，则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < b < a$ D、 $c < a < b$

查看试题解析
7. 已知函数 $f (x)$ 是R上的减函数， $A (- 1 ， 1)$ ， $B (3 ， - 1)$ 是其图象上的两点，那么 $| f (x - 1) | > 1$ 的解集是（）

A、 $(- \infty ， 0) ∪ (4 ， + \infty)$ B、 $(- \infty ， 0) ∪ (2 ， + \infty)$ C、 $(0 ， 4)$ D、 $(- \infty ， 0)$

查看试题解析
8. 中国高铁技术世界领先，高速列车运行时不仅速度比普通列车快且噪声更小．用声强I（单位： $W / m^{2}$ ）表示声音在传播途径中每平方米面积的声能流密度，声强级 $L_{I}$ （单位：dB）与声强Ⅰ的函数关系式为 $L_{I} = 10 l g \frac{I}{100}$ ．若普通列车的声强级是95dB，高速列车的声强级是45dB，则普通列车的声强是高速列车声强的（）

A、6倍 B、10倍 C、5倍 D、10倍

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 已知函数 $f (x) = {\begin{array}{l} 2^{x} + 1 ， x ≤ 0 \\ l o g_{2} x ， x > 0 \end{array}$ ，若 $f (x) = 2$ ，则 $x =$ （）

A、0 B、2 C、4 D、6

查看试题解析
10. 角 $θ$ 为第二象限角的充要条件是（）

A、 ${\begin{array}{l} s i n θ > 0 \\ c o s θ < 0 \end{array}$ B、 ${\begin{array}{l} s i n θ > 0 \\ t a n θ < 0 \end{array}$ C、 ${\begin{array}{l} c o s θ < 0 \\ t a n θ < 0 \end{array}$ D、 ${\begin{array}{l} c o s θ < 0 \\ s i n θ < 0 \end{array}$

查看试题解析
11. 已知 $α$ 为第二象限角，那么 $\frac{α}{3}$ 是（）

A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角

查看试题解析
12. 定义在 $(0 ， + \infty)$ 上的函数满足 $\frac{x_{2} f (x_{1}) - x_{1} f (x_{2})}{x_{1} - x_{2}} < 0$ ，且 $f (\frac{1}{2}) = 3$ ， $f (3) = 9$ ，则下列结论中正确的是（）

A、不等式 $f (x) > 3 x$ 的解集为 $(3 ， + \infty)$ B、不等式 $f (x) > 3 x$ 的解集为 $(0 ， 3)$ C、不等式 $f (x) < 6 x$ 的解集为 $(\frac{1}{2} ， + \infty)$ D、不等式 $f (x) < 6 x$ 的解集为 $(0 ， \frac{1}{2})$

查看试题解析

三、填空题：本大题共4小题，每小题5分，共20分．

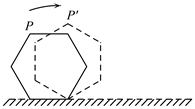
13. 函数 $f (x) = l o g_{a} (x - 2) + 2$ （ $a > 0$ 且 $a \neq 1$ ）的图象经过的定点是．

查看试题解析
14. 函数 $f (x) = a^{x}$ （ $a > 0$ 且 $a \neq 1$ ）的图象经过点 $(1 ， 10)$ ，则函数 $f (x)$ 的反函数 $g (x) =$ ．

查看试题解析
15. 函数 $f (x) = l n (x - a + 1)$ 的图象经过一、三、四象限，则a的取值范围是．

查看试题解析
16. 如图，边长为1的正六边形木块自图中实线标记位置起在水平桌面上从左向右做无滑动翻滚，点 $P$ 为正六边形的一个顶点，当点 $P$ 第一次落在桌面上时，点 $P$ 走过的路程为．

查看试题解析

四、解答题：本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

17. 计算：

(1)、 ${(\frac{27}{8})}^{- \frac{2}{3}} + π^{0} + l o g_{2} \frac{2}{3} - l o g_{4} \frac{16}{9}$ ；

(2)、 $10 c o s 270 ° + 4 s i n 0 ° + 9 t a n 60 ° + 15 c o s (- 360 °)$ 。

查看试题解析
18. 已知 $s i n α = \frac{2 \sqrt{2}}{3}$ 且 $α$ 为第二象限角．

(1)、求 $c o s α$ 和 $t a n α$ 的值；

(2)、若 $t a n β = \sqrt{2}$ ，求 $\frac{s i n α c o s β + 3 s i n (\frac{π}{2} + α) s i n β}{c o s (π + α) c o s (- β) - 3 s i n α s i n β}$ 的值．

查看试题解析
19.

(1)、已知函数 $f (x) = 2^{x}$ ， $x \in [\frac{1}{2} ， 2]$ ，求函数 $f (x)$ 的值域；

(2)、解关于x的不等式： $l o g_{a} (x + 1) < l o g_{a} (3 - x^{2})$ （ $a > 0$ 且 $a \neq 1$ ）。

查看试题解析
20. 已知二次函数 $f (x)$ 满足 $f (0) = 1$ ，且 $f (x + 1) - f (x) = 2 x - 1$ ， $g (x)$ 为偶函数，且当 $x ≥ 0$ 时， $g (x) = f (x)$ ．

(1)、求 $f (x)$ 的解析式；

(2)、在给定的坐标系内画出 $g (x)$ 的图象；

(3)、讨论函数 $h (x) = g (x) - t$ （ $t \in R$ ）的零点个数．

查看试题解析
21. 已知函数 $f (x) = \frac{3^{x} - 3^{- x}}{3^{x} + 3^{- x}}$ ．

(1)、判断函数 $f (x)$ 的奇偶性，并说明理由；

(2)、判断函数 $f (x)$ 在R上的单调性，并用单调性定义证明。

查看试题解析
22. 已知函数 $f (x) = 2^{x}$ ．

(1)、当 $x \in [0 ， 8]$ 时，不等式 $f (x + 1) ≥ f [(x + a)^{2}]$ 总成立，求a的取值范围；

(2)、试求函数 $G (x) = f (x + 1) + a f (2 x)$ （ $a \in R$ ）在 $x \in (- \infty ， 0]$ 的最大值 $H (a)$ ．

查看试题解析