贵州省铜仁市2023-2024学年高一上学期1月期末质量监测数学试题
试卷更新日期:2024-02-23 类型:期末考试
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知集合 , 则( )A、 B、 C、 D、2. ( )A、 B、 C、 D、3. 命题 , 则为( )A、 B、 C、 D、4. 已知 , 则它们的大小关系为( )A、 B、 C、 D、5. 已知幂函数的图象过点 , 下列说法正确的是( )A、 B、的定义域是 C、在上为减函数 D、为奇函数6. 设函数 , 则使得成立的的取值范围是( )A、 B、 C、 D、7. 设函数 , 若函数在上恰有3个零点,则正实数的取值范围是( )A、 B、 C、 D、8. 当时,不等式恒成立,则的取值范围是( )A、 B、 C、 D、
二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
-
9. 下列函数为偶函数的是( )A、 B、 C、 D、10. 已知 , 且 , 则( )A、 B、 C、 D、11. 如图某地一天从6时到14时的温度变化曲线近似满足函数 , 则( )
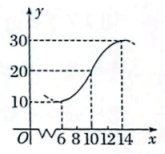 A、 B、 C、 D、这段曲线的解析式是12. 已知函数设的实数解个数为 , 则( )A、当时, B、当时, C、当时, D、函数的值域为
A、 B、 C、 D、这段曲线的解析式是12. 已知函数设的实数解个数为 , 则( )A、当时, B、当时, C、当时, D、函数的值域为三、填空题(本大题共4小题,每小题5分,共20分)
-
13. 已知 , 则 .14. 函数的最大值为 .15. 将函数的图象向右平移个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数的图象,则函数的解析式是 .16. 我们知道,函数的图象关于坐标原点成中心对称图形的充要条件是函数为奇函数,有同学发现可以将其推广为:“函数的图象关于点成中心对称图象的充要条件是函数为奇函数”,由此可得函数图象的对称中心是 .
四、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 已知集合 , 集合 .(1)、若 , 求;(2)、若集合满足条件:①;②;③是的必要条件.从以上三个条件中任选一个,求实数的取值范围.
注:如果选择多个条件分别解答,则按第一个解答计分.
18.(1)、计算 .(2)、某工厂生产一种溶液,按市场要求杂质含量不得超过 , 而这种溶液最初的杂质含量为 , 现进行过滤,已知每过滤一次杂质含量减少 , 求使产品达到市场要求的过滤的最少次数(参考数据:).