2024年人教版中考数学二轮复习专题1 实数

试卷更新日期：2024-02-23 类型：二轮复习

进入出卷网下载

一、选择题

1. 用 $5$ ， $0$ ， $5$ ， $5$ 这四个数进行如下运算，计算结果最小的式子是（）

A、 $5 - 0 \times 5 + 5$ B、 $5 - 0 + 5 \times 5$ C、 $5 \times 0 + 5 - 5$ D、 $5 + 0 - 5 \times 5$

查看试题解析
2. $(- 2)^{5}$ 是 $(- 2)^{3}$ 的（）倍．

A、 $2$ B、3 C、4 D、8

查看试题解析
3. 2023的相反数等于（）

A、2023 B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
4. 估计 $\sqrt{10} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 武汉市元月份某一天早晨的气温是-3℃，中午上升了8℃，则中午的气温是（）

A、-5℃ B、5℃ C、3℃ D、-3℃

查看试题解析
6. 下列四个数中，最小的是（）

A、 $- 3$ B、 $| - 7 |$ C、 $- (- 3)$ D、 $- \frac{1}{3}$

查看试题解析
7. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：
甲： $b - a ＜ 0$
乙： $a + b > 0$
丙： $| a | ＜ | b |$
丁： $\frac{b}{a} ＞ 0$
其中正确的是（）

A、甲乙 B、丙丁 C、甲丙 D、乙丁

查看试题解析
8. 如图，在数轴上，点A、B分别表示a、b ，且 $a + b = 0$ ，若 $A B = 6$ ，则点A表示的数为（）

A、 $- 3$ B、0 C、3 D、 $- 6$

查看试题解析
9. 若 $\sqrt{a - 4}$ 有意义，则 $a$ 的值可以是（）

A、-1 B、0 C、2 D、6

查看试题解析
10. 今年“十一”期间，广州部分公园举行游园活动，据统计，天河公园早晨 $6$ 时 $30$ 分有 $2$ 人进入公园，接下来的第一个 $30$ 分钟内有 $4$ 人进去 $1$ 人出来，第二个 $30$ 分钟内有 $8$ 人进去 $2$ 人出来，第三个 $30$ 分钟内有 $16$ 人进去 $3$ 人出来，第四个 $30$ 分钟内有 $32$ 人进去 $4$ 人出来．按照这种规律进行下去，到上午 $11$ 时 $30$ 分公园内的人数是（）

A、 $2^{11} - 47$ B、 $2^{12} - 57$ C、 $2^{13} - 68$ D、 $2^{14} - 80$

查看试题解析
11. 下列说法正确的有（　　）个．
①任何实数都可以开立方；②0的相反数、倒数、平方都是0；③数轴上的点和有理数一一对应；④有限小数和无限循环小数都是有理数；⑤无理数都是无限小数．

A、1 B、2 C、3 D、4

查看试题解析
12. 已知有理数 $a ， b ， c$ 满足 $a b c < 0$ ，则 $\frac{a}{| a |} + \frac{| b |}{b} + \frac{c}{| c |} - \frac{| a b c |}{a b c}$ 的值是（）

A、 $\pm 1$ B、0或2 C、 $\pm 2$ D、 $\pm 1$ 或 $\pm 2$

查看试题解析
13. 有一组非负整数： $a_{1}$ ， $a_{2}$ ， …， $a_{2022}$ ．从 $a_{3}$ 开始，满足 $a_{3} = | a_{1} - 2 a_{2} |$ ， $a_{4} = | a_{2} - 2 a_{3} |$ ， $a_{5} = | a_{3} - 2 a_{4} |$ ， …， $a_{2022} = | a_{2020} - 2 a_{2021} |$ ．某数学小组研究了上述数组，得出以下结论：
①当 $a_{1} = 2$ ， $a_{2} = 4$ 时， $a_{4} = 6$ ；
②当 $a_{1} = 3$ ， $a_{2} = 2$ 时， $a_{1} + a_{2} + a_{3} + ⋯ + a_{20} = 142$ ；
③当 $a_{1} = 2 x - 4$ ， $a_{2} = x$ ， $a_{5} = 0$ 时， $x = 10$ ；
④当 $a_{1} = m$ ， $a_{2} = 1$ （ $m \geq 3$ ， $m$ 为整数）时， $a_{2022} = 2020 m - 6059$ ．
其中正确的结论个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

14. 若 $| x + 10 | + (y - 9)^{2} = 0$ ，则 $(x + y)^{2023}$ 的值为．

查看试题解析
15. 如图，在数轴上点 $A$ ，点 $B$ 表示的数分别是 $- 5$ ， $3$ ，点 $P$ 在数轴上，若 $P A = 3 P B$ ，则点 $P$ 表示的数是．

查看试题解析
16. 已知m为正整数，若 $\sqrt{189 m}$ 是整数，则根据 $\sqrt{189 m} = \sqrt{3 \times 3 \times 3 \times 7 m} = 3 \sqrt{3 \times 7 m}$ 可知m有最小值 $3 \times 7 = 21$ .设n为正整数，若 $\sqrt{\frac{300}{n}}$ 是大于1的整数，则n的最小值为，最大值为.

查看试题解析
17. 若 $3 - \sqrt{2}$ 的整数部分为a，小数部分为b，则代数式 $(2 + \sqrt{2} a) \cdot b$ 的值是.

查看试题解析
18. 已知 $a$ 为有理数， ${a}$ 表示大于 $a$ 的最小整数，如 ${3} = 4 ， {\frac{2}{5}} = 1 ， {- 3 \frac{1}{2}} = - 3$ ，则计算 ${- 6 \frac{5}{6}} - {5} \times {- 1 \frac{3}{4}} \div {5.9} =$ ．

查看试题解析
19. 已知有理数a，b，c在数轴上的位置如图所示，满足|a|＜|b|＜|c|，则|2a+c﹣b|﹣|a﹣c+b|+ $\frac{a b}{| a b |} - \frac{| a c |}{a c}$ ＝．

查看试题解析
20. 设有理数a，b，c满足a+b+c=0，abc> 0，则a，b，c中正数的个数为

查看试题解析
21. 已知 $\frac{x y z}{| x y z |} = 1$ ，则 $\frac{| x |}{x} + \frac{y}{| y |} + \frac{| z |}{z}$ 值为．

查看试题解析

三、计算题

22. 计算题：

(1)、 $3 - 5 - | 4 - 6 | + 2$ ；

(2)、 $- 1^{2024} + 8 \div {(- \frac{2}{3})}^{3} \times | 2023 - 2024 |$ ．

查看试题解析
23. 计算：

(1)、 $(- 24) \times (\frac{1}{8} - \frac{1}{3} + \frac{1}{4})$ ；

(2)、 $\sqrt[3]{- 8} + \sqrt{25} \times (- 2)^{2}$ ．

查看试题解析

四、解答题

24. 阅读下面的解题过程，判断是否正确.若不正确，请写出正确的解答过程.
已知m为实数，化简 $： - \sqrt{- m^{3}} + m^{2} \sqrt{- \frac{1}{m}} .$
解：原式 $= - m \sqrt{- m} + m^{2} \cdot \frac{1}{m} \sqrt{- m} = 0 .$

查看试题解析
25. 已知 $m = \sqrt{n - 5} - \sqrt{5 - n} + 4 .$

(1)、求m，n的值.

(2)、若关于x的一元二次方程 $m x^{2} + b x + n = 0$ 有一个根是1，求b的值.

查看试题解析
26. 已知m为正整数，若 $\sqrt{189 m}$ 是整数，则根据 $\sqrt{189 m} = \sqrt{3 \times 3 \times 3 \times 7 m} = 3 \sqrt{3 \times 7 m} ，$ 可知m有最小值3×7=21.
设n为正整数，若 $\sqrt{\frac{300}{n}}$ 是大于1的整数，求n的最小值和最大值

查看试题解析

五、实践探究题

27. 阅读下面内容：我们已经学习了《二次根式》和《乘法公式》，聪明的你可以发现：当 $a > 0$ ， $b > 0$ 时，∵ ${(\sqrt{a} - \sqrt{b})}^{2} = a - 2 \sqrt{a b} + b \geq 0$ ， ∴ $a + b \geq 2 \sqrt{a b}$ ，当且仅当 $a = b$ 时取等号，
例如：当 $a > 0$ 时，求 $a + \frac{4}{a}$ 的最小值．
解∵ $a > 0$ ∴ $a + \frac{4}{a} \geq 2 \sqrt{a \cdot \frac{16}{a}}$ 又∵ $2 \sqrt{a \cdot \frac{4}{a}} = 4$ ， ∴ $a + \frac{4}{a} \geq 4$ ，即 $a = 2$ 时取等号．
∴ $a + \frac{4}{a}$ 的最小值为4．
请利用上述结论解决以下问题：

(1)、当 $x > 0$ 时，当且仅当 $x =$ 时， $x + \frac{1}{x}$ 有最小值．

(2)、当 $m > 0$ 时，求 $\frac{m^{2} + 5 m + 12}{m}$ 的最小值．

(3)、请解答以下问题：
如图所示，某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙足够长），另外三边用篱笆围成，设垂直于墙的一边长为x米．若要围成面积为200平方米的花围，需要用的篱笆最少是多少米？

查看试题解析

六、综合题

28. 数轴上点A表示数a ，点B表示数b ，且a ， b满足 $| a + 1 | + {(b - 5)}^{2} = 0$ ．一只蚂蚁从点A出发沿数轴以每秒2个单位长度的速度向右爬行，爬行时间为t秒．

(1)、求出a ， b的值．

(2)、若蚂蚁爬行t秒，正好到达点C ，则点C所表示的数为．（用含t的式子表示）．

(3)、若蚂蚁爬行到点D时，到点A ， B的距离相等，则爬行时间t=秒．

(4)、若蚂蚁从点A出发时，恰好有一只甲壳虫同时从点B出发沿数轴以每秒1个单位长度的速度向右爬行，经过一段时间后，蚂蚁和甲壳虫相距2个单位长度，请求出爬行时间t的值．

查看试题解析
29. 如图，数轴上A，B两点表示的有理数分别为a、b，满足 $| a + 8 | + {(b - 4)}^{2} = 0$ ，原点O是线段AB上的一点.

(1)、a= ， b= ， AB= ；

(2)、若动点P，Q分别从A，B同时出发，向右运动，点P的速度为每秒2个单位长度，点Q的速度为每秒1个单位长度，设运动时间为t秒，当t为何值时，BP=2BQ？

(3)、若点P、Q仍按（2）中速度运动，当点P与点Q重合时停止运动，当点P到达点O时，动点M从点O出发，以每秒3个单位长度的速度也向右运动，当点M追上点Q后立即返回，以同样的速度向点P运动，遇到点P后再立即返回，以同样的速度向点Q运动，如此往返，直到点P，Q停止时，点M也停止运动，求在此过程中M点行驶的总路程，并直接写出点M最后位置在数轴上所对应的有理数.

查看试题解析
30. 如图1，点 $A ， B ， C$ 是数轴上：从左到右排列的三个点，分别对应的数为 $- 5 ， b ， 4.$ 某同学将刻度尺如图2放置.使刻度尺上的数字 $0$ 对齐数轴上的点 $A$ ，发现点 $B$ 对齐刻度 $1.8 c m$ ，点 $C$ 对齐刻度 $5.4 c m$ .

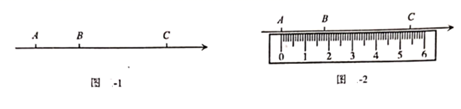(1)、在图1的数轴上， $A C =$ 个单位长度；数轴上的一个单位长度对应刻度尺上的 $c m$ .

(2)、求数轴上点 $B$ 所对应的数 $b$ ；

(3)、在图1的数轴上，点 $Q$ 是线段 $A B$ 上一点，满足 $A Q = 2 Q B ，$ 求点 $Q$ 所表示的数.

查看试题解析

2024年人教版中考数学二轮复习 专题1 实数

一、选择题

二、填空题

三、计算题

四、解答题

五、实践探究题

六、综合题

2024年人教版中考数学二轮复习专题1 实数