广东省深圳市龙岗区2023-2024学年高一上学期1月期末质量监测数学试题

试卷更新日期：2024-02-23 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 $s i n 420 °$ 的值是（）

A、 $- \frac{\sqrt{3}}{2}$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 设集合M=｛x|0＜x＜4｝，N=｛x| $\frac{1}{3}$ ≤x≤5｝，则M∩N=（）

A、｛x|0＜x≤ $\frac{1}{3}$ ｝ B、｛x| $\frac{1}{3}$ ≤x＜4｝ C、｛x|4≤x＜5｝ D、｛x|0＜x≤5｝

查看试题解析
3. 当a>1时，在同一直角坐标系中，函数 $y = a^{- x}$ 与 $y = l o g_{a} x$ 的图像是（）

A、 B、 C、 D、

查看试题解析
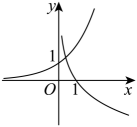4. 已知命题“ $\forall x \in R ， x^{2} + (a - 2) x + \frac{9}{4} > 0$ ”是真命题，则实数a的取值范围是（）

A、 $(- \infty ， - 1)$ B、 $(- 5 ， 1)$ C、 $(- 5 ， + \infty)$ D、 $(- 1 ， 5)$

查看试题解析
5. “ $c o s θ > 0$ 且 $s i n 2 θ < 0$ ”是“ $θ$ 为第四象限角”的（）

A、充要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件

查看试题解析
6. 已知 $f (x) = x^{5} + a x^{3} + b x + 3$ 且 $f (- 2) = 5$ ，则 $f (2)$ 的值是（）

A、 $- 3$ B、 $- 1$ C、1 D、3

查看试题解析
7. 已知角 $α \in (0 ， 2 π)$ ， $α$ 终边上有一点 $(c o s 1 - s i n 1 ， c o s 1 + s i n 1)$ ，则 $α =$ （）

A、 $\frac{π}{4} + 1$ B、 $\frac{5 π}{4} - 1$ C、 $\frac{9 π}{4}$ D、 $\frac{9 π}{4} - 1$

查看试题解析
8. 设函数 $f (x) = {\begin{array}{l} 3^{x} ， x \leq 0 \\ l o g_{3} x ， x > 0 \end{array}$ ，对任意给定的 $m \in (1 ， + \infty)$ ，都存在唯一的 $x \in R$ ，使得 $f (f (x)) = m^{2} + 2 a m - 3 (a > 0)$ 成立，则a的最小值是（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、2

查看试题解析

二、多选题

9. 已知a ， b ， c为实数，则下列命题中正确的是（）

A、若 $\frac{a}{c^{2}} < \frac{b}{c^{2}}$ ，则 $a < b$ B、若 $a c > b c$ ，则 $a > b$ C、若 $a > b$ ， $c > d$ ，则 $a + c > b + d$ D、若 $a < b < 0$ ，则 $\frac{1}{a} > \frac{1}{b}$

查看试题解析
10. 在 $△ A B C$ 中，下列等式恒成立的是（）

A、 $s i n (A + B) - s i n C = 0$ B、 $c o s (B + C) - c o s A = 0$ C、 $\frac{s i n \frac{A + B}{2}}{c o s \frac{C}{2}} = 1$ D、 $\frac{c o s \frac{B + C}{2}}{c o s \frac{A}{2}} = 1$

查看试题解析
11. $0 < α < β < \frac{π}{2}$ ， $t a n α$ 和 $t a n β$ 是方程 $x^{2} - m x + 2 = 0$ 的两个根，则下列结论正确的是（）

A、 $t a n α + t a n β = m$ B、 $t a n (α + β) > 0$ C、 $m \geq 2 \sqrt{2}$ D、 $m + t a n α \geq 4$

查看试题解析
12. 设 $f (x) = {\begin{array}{l} - \frac{2}{x} ， x < 0 \\ {(x - 1)}^{2} ， x \geq 0 \end{array}$ ，则下列选项中正确的有（）

A、 $y = f (x)$ 与 $y = a ， a \in R$ 的图象有两个交点，则 $a \in (1 ， + \infty)$ B、方程 $f (x) - m = 0$ 有三个实数根，则 $m \in (0 ， 1]$ C、 $f (x) \geq 1$ 的解集是 $[2 ， + \infty)$ D、 $0 \leq f (f (x)) \leq 1$ 的解集是 $(- \infty ， - 1] ∪ [0 ， \sqrt{2} + 1]$

查看试题解析

三、填空题

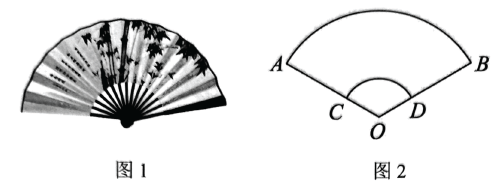
13. 函数 $f (x) = \sqrt{2 - x} + l n x$ 的定义域是.

查看试题解析
14. 如图1，折扇又名“撒扇”“纸扇”，是一种用竹木或象牙做扇骨，㓞纸或绫绢做扇面的能折叠的扇子，其展开的平面图如图2的扇形AOB ，其中 $∠ A O B = 150 °$ ， $C O = \frac{1}{3} A O = 2$ ，则扇面（曲边四边形ABDC）的面积是．

查看试题解析
15. 设 $a = l o g_{3} 0.3 ， b = l o g_{\frac{1}{3}} 0.2 ， c = 0 . 2^{0.3}$ ，则a ， b ， c的大小关系为．

查看试题解析
16. 对任意 $x ∈ R$ ，恒有 $f (1 - x) = f (x + 1) = f (x - 1)$ ，对任意 $θ \in [0 ， \frac{π}{2}] ， f (s i n θ) = c o s^{2} θ$ ，现已知函数 $y = f (x)$ 的图像与 $y = k x$ 有4个不同的公共点，则正实数 $k$ 的值为.

查看试题解析

四、解答题

17. 已知集合 $A = {x | - 3 \leq x \leq 2}$ ，集合 $B = {x | 1 - m \leq x \leq 3 m - 1}$ ．

(1)、当 $m = 3$ 时，求 $(∁_{R} A) ∩ B$ ；

(2)、若 $A ⊆ B$ ，求实数m的取值范围．

查看试题解析
18. 函数 $f (x) = A c o s (ω x + φ)$ （其中 $A > 0 ， ω > 0 ， | φ | < \frac{π}{2}$ ）的部分图象如图所示，先把函数 $f (x)$ 的图象上的各点的横坐标缩短为原来的 $\frac{1}{2}$ （纵坐标不变），把得到的曲线向左平移 $\frac{π}{4}$ 个单位长度，再向上平移1个单位，得到函数 $g (x)$ 的图象．

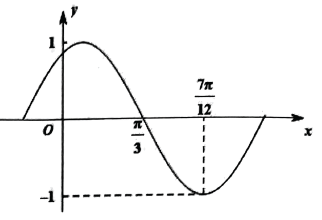(1)、求函数 $g (x)$ 图象的对称中心；

(2)、当 $x \in [- \frac{π}{8} ， \frac{π}{8}]$ 时，求 $g (x)$ 的值域．

查看试题解析
19. 已知函数 $f (x) = \frac{a x + b}{x^{2} + 1}$ 是定义在 $(- 1 ， 1)$ 上的奇函数，且 $f (\frac{1}{2}) = \frac{2}{5}$ .

(1)、求函数 $f (x)$ 的解析式；

(2)、判断函数 $f (x)$ 在 $(- 1 ， 1)$ 上的单调性，并用定义证明；

(3)、解关于 $t$ 的不等式， $f (t + \frac{1}{2}) + f (t - \frac{1}{2}) < 0$ .

查看试题解析
20. 已知函数 $f (x) = s i n (2 x - \frac{π}{6}) - c o s 2 x$ ， $x ∈ R$ .

(1)、求函数 $f (x)$ 的最小正周期；

(2)、求函数 $f (x)$ 的对称轴方程；

(3)、求函数 $f (x)$ 在 $[0 ， \frac{π}{2}]$ 上的单调区间.

查看试题解析
21. 党的二十大报告指出：必须坚持科技是第一生产力、人才是第一资源、创新是第一动力．科技兴则民族兴，科技强则国家强.2023年9月，华为Mate60系列的发布再次引发了广泛关注，它不仅展示了中国科技产业的不断进步和发展，更体现了中国人民自主创新、顽强不屈的精神．某芯片企业原有400名技术人员，年人均投入 $a$ 万元 $(a > 0)$ ，现为加大对研发工作的投入，该企业把原有技术人员分成技术人员和研发人员，其中技术人员 $x$ 名，调整后研发人员的年人均投入增加 $(4 x) %$ ，技术人员的年人均投入调整为 $a (m - \frac{2 x}{25})$ 万元．

(1)、若要使调整后研发人员的年总投入不低于调整前400名技术人员的年总投入，求调整后的研发人员的人数最少为多少人？

(2)、为了激励研发人员的工作热情和保持技术人员的工作积极性，企业决定在投入方面要同时满足以下三个条件：①技术人员不少于100人，不多于275人；②研发人员的年总投入始终不低于技术人员的年总投入；③技术人员的年人均投入始终不减少．请问是否存在这样的实数 $m$ ，满足以上两个条件，若存在，求出 $m$ 的范围；若不存在，说明理由．

查看试题解析
22. 已知函数 $f (x) = 9^{x} - 2 \cdot 3^{x + m} (m > 0)$ ．

(1)、当 $m = 1$ 时，求不等式 $f (x) \leq 27$ 的解集；

(2)、若 $x_{2} > x_{1} > 0$ 且 $x_{1} x_{2} = m^{2}$ ，试比较 $f (x_{1})$ 与 $f (x_{2})$ 的大小关系；

(3)、令 $g (x) = f (x) + f (- x)$ ，若 $y = g (x)$ 在R上的最小值为 $- 11$ ，求m的值

查看试题解析