广东省茂名市2023-2024学年高三一模数学试题
试卷更新日期:2024-02-23 类型:高考模拟
一、单选题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知集合 , , , 则集合的子集个数为( )A、2 B、3 C、4 D、82. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 从6名女生3名男生中选出2名女生1名男生,则不同的选取方法种数为( )A、33 B、45 C、84 D、904. 曲线在点处的切线与直线平行,则( )A、 B、 C、1 D、25. 椭圆:()的左、右焦点分别为 , , 过作垂直于轴的直线 , 交于 , 两点,若 , 则的离心率为( )A、 B、 C、 D、6. 函数和均为上的奇函数,若 , 则( )A、 B、 C、0 D、27. 若 , , 则( )A、 B、 C、 D、8. 数列满足 , (), , 若数列是递减数列,则实数的取值范围是( )A、 B、 C、 D、
二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
9. 若是区间上的单调函数,则实数的值可以是( )A、 B、 C、3 D、410. 过抛物线:的焦点作直线 , 交于 , 两点,则( )A、的准线方程为 B、以为直径的圆与的准线相切 C、若 , 则线段中点的横坐标为 D、若 , 则直线有且只有一条11. 在棱长为2的正方体中, , 分别为棱 , 的中点,则( )A、直线与所成的角为60° B、过空间中一点有且仅有两条直线与所成的角都是60° C、过 , , 三点的平面截该正方体,所得截面图形的周长为 D、过直线的平面截正方体,所得截面图形可以是五边形12. 从标有1,2,3,…,10的10张卡片中,有放回地抽取两张,依次得到数字 , , 记点 , , , 则( )A、是锐角的概率为 B、是锐角的概率为 C、是锐角三角形的概率为 D、的面积不大于5的概率为
三、填空题:本大题共4小题,每小题5分,共20分.
-
13. 已知复数 , 其中为虚数单位,则.14. 如图,茂名的城市雕像“希望之泉”是茂名人为了实现四个现代化而努力奋斗的真实写照.被托举的四个球堆砌两层放在平台上,下层3个,上层1个,两两相切.若球的半径都为 , 则上层的最高点离平台的距离为.
 15. 动点与两个定点 , 满足 , 则点到直线:的距离的最大值为.16. 函数()在区间上有且只有两个零点,则的取值范围是.
15. 动点与两个定点 , 满足 , 则点到直线:的距离的最大值为.16. 函数()在区间上有且只有两个零点,则的取值范围是.四、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.
-
17. 在中,角 , , 所对的边分别为 , , , 已知.(1)、求的值;(2)、若为的中点,且 , 求的最小值.18. 已知某种业公司培育了新品种的软籽石榴,从收获的果实中随机抽取了50个软籽石榴,按质量(单位:)将它们分成5组: , , , , 得到如下频率分布直方图.
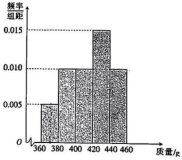 (1)、用样本估计总体,求该品种石榴的平均质量;(同一组中的数据用该组区间的中点值作代表)(2)、按分层随机抽样,在样本中,从质量在区间 , , 内的石榴中抽取7个石榴进行检测,再从中抽取3个石榴作进一步检测.
(1)、用样本估计总体,求该品种石榴的平均质量;(同一组中的数据用该组区间的中点值作代表)(2)、按分层随机抽样,在样本中,从质量在区间 , , 内的石榴中抽取7个石榴进行检测,再从中抽取3个石榴作进一步检测.(ⅰ)已知抽取的3个石榴不完全来自同一区间,求这3个石榴恰好来自不同区间的概率;
(ⅱ)记这3个石榴中质量在区间内的个数为 , 求的分布列与数学期望.
19. 已知数列的前项和为 , 数列是首项为、公差为的等差数列.(1)、求的通项公式;(2)、令 , 为数列的前项积,证明: , .20. 如图,在四棱锥中,平面平面 , , , , , .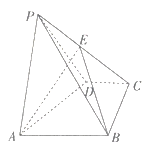 (1)、证明:;(2)、点在线段上,当直线与平面所成角的正弦值为时,求平面与平面的夹角的余弦值.
(1)、证明:;(2)、点在线段上,当直线与平面所成角的正弦值为时,求平面与平面的夹角的余弦值.