2023年吉林省中考数学真题变式题:第八题
试卷更新日期:2024-02-23 类型:二轮复习
一、原题重现
-
1. 不等式的解集为 .
二、变式基础练
-
2. 当x满足x+1<3x-3时,方程=0的根为.3. 一个不等式的解表示在数轴上如图所示,则这个不等式可以是( )
 A、2x≥6 B、x-3<0 C、3-x<0 D、x+3>04. 解不等式:的解集是 .5. 3x-5<1的正整数解为.6. 关于的不等式的解集是.7. 不等式 的解为.8. 不等式2x﹣3≥5x﹣10的所有正整数解的和为 .9. 解不等式组,并把解集在数轴上表示出来: .
A、2x≥6 B、x-3<0 C、3-x<0 D、x+3>04. 解不等式:的解集是 .5. 3x-5<1的正整数解为.6. 关于的不等式的解集是.7. 不等式 的解为.8. 不等式2x﹣3≥5x﹣10的所有正整数解的和为 .9. 解不等式组,并把解集在数轴上表示出来: .
三、变式提升练
-
10. 不等式 的解集在数轴上表示正确的是( )A、
 B、
B、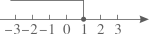 C、
C、 D、
D、 11. 关于的方程解为负数,则实数a的取值范围是( ).A、 B、 C、 D、12. 已知关于的分式方程的解是非负数.则的取值范围是( )A、 B、 C、且 D、且13. 若不等式(a﹣3)x>1的解集为 , 则a的取值范围是 .14. 已知方程组的解满足 , 求的取值范围.15. 解下列方程或不等式 .(1)、;
11. 关于的方程解为负数,则实数a的取值范围是( ).A、 B、 C、 D、12. 已知关于的分式方程的解是非负数.则的取值范围是( )A、 B、 C、且 D、且13. 若不等式(a﹣3)x>1的解集为 , 则a的取值范围是 .14. 已知方程组的解满足 , 求的取值范围.15. 解下列方程或不等式 .(1)、;
(2)、 .16. 解不等式(组),并把解集在数轴上表示出来.(1)、(2)、四、变式培优练
-
17. 对于实数、 , 且 , 我们用符号表示、两数中较小的数,如 . 若 , 则 .18. 新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程的解为 , 而不等式组的解集为 , 不难发现在的范围内,所以方程是不等式组的“关联方程”.(1)、在方程①;②;③中,不等式组的“关联方程”是;(填序号)(2)、关于x的方程是不等式组的“关联方程”,求k的取值范围;(3)、若关于x的方程是关于x的不等式组的“关联方程”,且此时不等式组有3个整数解,试求m的取值范围.19. 阅读下列材料:
我们给出如下定义:数轴上给定不重合两点A , B , 若数轴上存在点M , 使得点M到点A的距离等于点M到点B的距离的2倍,则称点M为点A与点B的“亚运点”.其中在A,B之间的点M为点A与点B的“亚运@未来点”
解答下列问题:
(1)、若点A表示的数为-5,点B表示的数为1,点M为点A与点B的“亚运点”,则点M表示的数为;(2)、若A、B两点的“亚运点”M表示的数为2,且A、B两点的距离为9(A在B的左侧),则点A表示的数为 ,(3)、点A表示的数为-6,点C , D表示的数分别是-2,0,点O为数轴原点(与静止时的D点重合),点B为线段CD上一点(点B可以与点C与点D重合).①设点M表示的数为m , 若点M可以为点A与点B的“亚运@未来点”,则m可取得整数有;
②若点A和点D同时以每秒2个单位长度的速度向数轴正半轴方向移动.设移动的时间为t(t>0)秒,当t的整数值为时,点O可以为点A与点B的“亚运@未来点”.
20. 定义:若一元一次方程的解在一元一次不等式的解集范围内,则称一元一次方程为一元一次不等式的“伴随方程”.如:一元一次方程的解为 , 而一元一次不等式的解集为 , 不难发现在范围内,则一元一次方程是一元一次不等式的“伴随方程”(1)、在① , ② , ③三个一元一次方程中,是一元一次不等式的“伴随方程”的有(填序号);(2)、若关于x的一元一次方程是关于x一元一次不等式的“伴随方程”,且一元一次方程不是关于x的一元一次不等式的“伴随方程”.①求a的取值范围;
②直接写出代数式的最大值.
21. 阅读理解:定义:使方程(组)与不等式(组)同时成立的未知数的值称为此方程(组)和不等式(组)的“理想解”.例如:已知方程与不等式 , 当时, , 同时成立,则称“”是方程与不等式的“理想解”.
问题解决:
(1)、请判断方程的解是此方程与以下哪些不等式(组)的“理想解”(直接填写序号)① ,
② ,
③;
(2)、若是方程组与不等式的“理想解”,求q的取值范围;(3)、当时,方程的解都是此方程与不等式的“理想解”.若且满足条件的整数n有且只有一个,求m的取值范围.
-