2023年吉林省中考数学真题变式题:第六题
试卷更新日期:2024-02-23 类型:二轮复习
一、原题重现
-
1. 如图, , 是的弦, , 是的半径,点为上任意一点(点不与点重合),连接 . 若 , 则的度数可能是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、变式基础练
-
2. 如图,圆周角∠ACB =48°,则圆心角∠AOB的度数为( ).
 A、48° B、24° C、96° D、90°3. 如图,点A,B,C都在⊙O上,若∠BAC=38°,则∠BOC的度数为( )
A、48° B、24° C、96° D、90°3. 如图,点A,B,C都在⊙O上,若∠BAC=38°,则∠BOC的度数为( )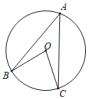 A、80° B、76° C、62° D、52°4. 如图,是的直径.若 , , 则长等于( )
A、80° B、76° C、62° D、52°4. 如图,是的直径.若 , , 则长等于( ) A、 B、 C、4 D、55. 如图,点A , B , C均在⊙O上,若∠A=68°,则∠OCB=( )
A、 B、 C、4 D、55. 如图,点A , B , C均在⊙O上,若∠A=68°,则∠OCB=( ) A、22° B、23° C、24° D、28°6. 如图,四边形是的内接四边形,是的直径, , 则的度数是 .
A、22° B、23° C、24° D、28°6. 如图,四边形是的内接四边形,是的直径, , 则的度数是 . 7. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .
7. 如图,四边形内接于 , 延长至点 , 已知 , 那么 .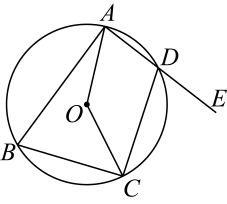 8. 如图, 是 的外接圆,直径 , ,则 长为.
8. 如图, 是 的外接圆,直径 , ,则 长为.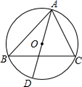 9. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=70°,PA , PC是⊙O的切线,∠P=°.
9. 如图,AB是⊙O的直径,点C在⊙O上,∠ABC=70°,PA , PC是⊙O的切线,∠P=°. 10. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=.
10. 如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC=.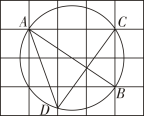
三、变式提升练
-
11. 如图,是的直径,点C、D、E在上,若 , , 且 , 则为( )
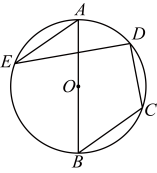 A、 B、6 C、 D、12. 如图,是的直径,C、D是上两点, , 则等于( )
A、 B、6 C、 D、12. 如图,是的直径,C、D是上两点, , 则等于( ) A、 B、 C、 D、13. 如图,在△ABC中,∠A=30°,∠C=45°,BC=2,则的长度为( )
A、 B、 C、 D、13. 如图,在△ABC中,∠A=30°,∠C=45°,BC=2,则的长度为( ) A、 B、 C、π D、2π14. 如图,在⊙O中,直径AB与弦CD相交于点P,连结AC,AD,BD.若∠C=20°,∠BPC=70°,则∠ADC=( )
A、 B、 C、π D、2π14. 如图,在⊙O中,直径AB与弦CD相交于点P,连结AC,AD,BD.若∠C=20°,∠BPC=70°,则∠ADC=( ) A、70° B、60° C、50° D、40°15. 如图,四边形ABCD内接于⊙O,连结OB,OD,BD.若∠C=110°,则∠OBD=( )
A、70° B、60° C、50° D、40°15. 如图,四边形ABCD内接于⊙O,连结OB,OD,BD.若∠C=110°,则∠OBD=( ) A、15° B、20° C、25° D、30°16. 如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=( )
A、15° B、20° C、25° D、30°16. 如图,AB是⊙O的直径,C是⊙O上一点.若∠BOC=66°,则∠A=( ) A、66° B、33° C、30° D、24°17. 如图,AB是⊙O的直径,弦CD交AB于点E,连结AC,AD.若∠BAC=28°,则∠D=°.
A、66° B、33° C、30° D、24°17. 如图,AB是⊙O的直径,弦CD交AB于点E,连结AC,AD.若∠BAC=28°,则∠D=°. 18. 如图,△ABC内接于⊙O,圆的半径为7,∠BAC=60°,则弦BC的长为.
18. 如图,△ABC内接于⊙O,圆的半径为7,∠BAC=60°,则弦BC的长为. 19. 如图,以△ABC的边AB为直径作⊙O,分别交AC,BC两边于点D,E,连结ED,且ED=EC.
19. 如图,以△ABC的边AB为直径作⊙O,分别交AC,BC两边于点D,E,连结ED,且ED=EC.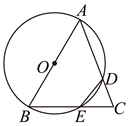 (1)、求证:AB=AC.(2)、若AB=4,BC= ,求CD的长.20. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)
(1)、求证:AB=AC.(2)、若AB=4,BC= ,求CD的长.20. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)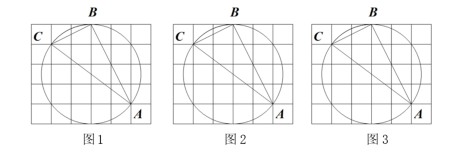 (1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.
(1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.四、变式培优练
-
21. 如图,⊙O是等边三角形ABC的外接圆,D是AC上一动点(不与点A,C重合),有下列结论:①∠ADB=∠BDC;②DA=DC;③当DB最长时,DB=2DC;④DA+DC=DB,其中一定正确的结论是( )
 A、①②. B、①③ C、③④ D、①③④22. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( )
A、①②. B、①③ C、③④ D、①③④22. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( ) A、 B、 C、 D、23. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )
A、 B、 C、 D、23. 在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点Р是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值为( )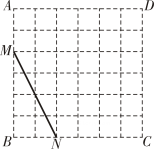 A、 B、6 C、 D、24. 如图,△ABD内接于半径为5的⊙O,连结AO并延长交BD于点M,交⊙O于点C,过点A作AE// BD,交CD的延长线于点E,AB=AM.
A、 B、6 C、 D、24. 如图,△ABD内接于半径为5的⊙O,连结AO并延长交BD于点M,交⊙O于点C,过点A作AE// BD,交CD的延长线于点E,AB=AM. (1)、求证:△ABM∽△ECA.(2)、当CM=4OM时,求AD的长.(3)、当CM= kOM时,设△MCD的面积为S1 , △ADE的面积为S2 ,求的值(用含k的代数式表示).25. 如图,AB为⊙O的直径,C为⊙O上一点,连结AC,BC.过点C作⊙O的切线,交AB的延长线于点D,OF⊥BC于点E,交CD于点F.
(1)、求证:△ABM∽△ECA.(2)、当CM=4OM时,求AD的长.(3)、当CM= kOM时,设△MCD的面积为S1 , △ADE的面积为S2 ,求的值(用含k的代数式表示).25. 如图,AB为⊙O的直径,C为⊙O上一点,连结AC,BC.过点C作⊙O的切线,交AB的延长线于点D,OF⊥BC于点E,交CD于点F. (1)、求证;∠BCD=∠BOE.(2)、若 , 求BD的长.
(1)、求证;∠BCD=∠BOE.(2)、若 , 求BD的长.
-