【培优卷】2024年浙教版数学七年级下册2.4二元一次方程组的应用同步练习

试卷更新日期：2024-02-23 类型：同步测试

进入出卷网下载

一、选择题

1. 篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分，某队在8场比赛中得到12分，那么这个队胜的场数是（）

A、3场 B、4场 C、5场 D、6场

查看试题解析
2. 某学校为了增强学生体质，决定让各班去购买跳绳和毽子作为活动器械.七年1班生活委员小亮去购买了跳绳和毽子共5件，已知两种活动器械的单价均为正整数且跳绳的单价比毽子的单价高.在付款时，小亮问是不是30元，但收银员却说一共45元，小亮仔细看了看后发现自己将两种商品的单价记反了，则小亮实际购买情况是（）

A、1根跳绳，4个毽子 B、3根跳绳，2个毽子 C、2根跳绳，3个毽子 D、4根跳绳，1个毽子

查看试题解析
3. 用如图①中的长方形和正方形纸板作侧面和底面，做成如图②的竖式和横式的两种无盖纸盒现在仓库里有m张正方形纸板和n张长方形纸板，如果做两种纸盒若干个，恰好使库存的纸板用完，则 $m + n$ 的值可能是（）

A、2023 B、2024 C、2025 D、2026

查看试题解析
4. 现有如图①的小长方形纸片若干块，已知小长方形的长为a，宽为b．用3个如图②的图形和8个如图①的小长方形，拼成如图③的大长方形，若大长方形的宽为30cm，则图③中阴影部分面积与整个图形的面积之比为（）．

A、 $\frac{1}{5}$ B、 $\frac{1}{6}$ C、 $\frac{1}{7}$ D、 $\frac{1}{8}$

查看试题解析
5. 如图，已知直线 $l_{1} ∥ l_{2}$ ， $∠ A = 125 °$ ， $∠ B = 85 °$ ，且 $∠ 1$ 比 $∠ 2$ 大 $4 °$ ，那么 $∠ 1$ 的大小是（）

A、 $13 °$ B、 $15 °$ C、 $16 °$ D、 $17 °$

查看试题解析
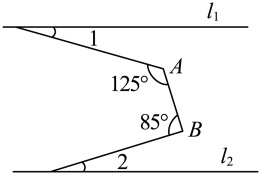6. 某份资料计划印制1000份，该任务由A，B两合印刷机先后接力完成，A印刷机印制 $150 份 / h$ ， B印刷机印制 $200 份 / h$ ．两台印刷机完成该任务共需 $6 h$ ．甲、乙两人所列的方程组如图所示，下列判断正确的是（）

A、只有甲列的方程组正确 B、只有乙列的方程组正确 C、甲和乙列的方程组都正确 D、甲和乙列的方程组都不正确

查看试题解析
7. 某校的劳动实践基地有一块长为10m，宽为8m的长方形空地，学校准备在这块空地上沿平行于长方形各边的方向割出3个大小和形状完全相同的小长方形菜地（图中阴影部分）分别种上辣椒、茄子、土豆，如图所示，则每个小长方形菜地的面积是（）

A、 $10 m^{2}$ B、 $9 m^{2}$ C、 $8 m^{2}$ D、 $7 m^{2}$

查看试题解析
8. 如图，把一个周长为定值的长方形（长小于宽的3倍）分割为五个四边形，其中A是正方形，周长记为 $l_{1}$ ， B和D是完全一样的长方形，周长记为 $l_{2}$ ， C和E是完全一样的正方形，周长记为 $l_{3}$ ，下列为定值的是（）

A、 $l_{1} ， l_{2}$ B、 $l_{1} ， l_{3}$ C、 $l_{2} ， l_{3}$ D、 $l_{1} ， l_{2} ， l_{3}$

查看试题解析

二、填空题

9. 已知 ${\begin{array}{l} x = - 2 \\ y = 3 \end{array}$ 和 ${\begin{array}{l} x = 4 \\ y = 1 \end{array}$ 是二元一次方程 $a x - 3 b y = 5$ 的两个解，则 $a + b =$ ．

查看试题解析
10. 三个同学对问题“若方程组 ${\begin{matrix} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{matrix}$ 的解是 ${\begin{matrix} x = 3 \\ y = 4 \end{matrix}$ ，求方程组 ${\begin{matrix} 3 a_{1} x + 2 b_{1} y = 5 c_{1} \\ 3 a_{2} x + 2 b_{2} y = 5 c_{2} \end{matrix}$ 的解．”提出各自的想法。甲说：“这个题目好像条件不够，不能求解”；乙说：“它们的系数有一定的规律，可以试试”；丙说：“能不能把第二个方程组的两个方程的两边都除以5，通过换元替换的方法来解决”．参考他们的讨论，你认为这个题目的解应该是．

查看试题解析
11. 如下图所示，高速公路上，一辆长为4米，速度为110千米/时的轿车准备超越一辆长为12米，速度为100千米/时的卡车，则轿车从开始追赶到超越卡车，需要花费的时间约是秒（结果保留整数）.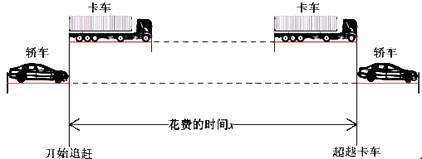

查看试题解析
12. 长方形ABCD中放入六个长、宽都相同的小长方形，所标尺寸如图所示，则小长方形的宽CE为cm．

查看试题解析

三、解答题

13. 国家实行一系列“三农”优惠政策后，使农民收入大幅度增加，也调动了农民生产积极性．某农业基地去年种植蔬菜和茶叶的总收入是 $3400$ 万元，今年扩大了蔬菜和茶叶的种植面积，这样按照去年的平均每亩收入，预计今年蔬菜和茶叶的种植总收入将比去年增加 $800$ 万元，其中蔬菜的种植收入将增加 $20 %$ ，茶叶种植收入将增加 $30 %$ ．

(1)、问该农业基地去年种植蔬菜和茶叶的收入各是多少万元？

(2)、经测算茶叶平均每亩的收入要比蔬菜平均每亩的收入多 $0.2$ 万元，日常管理中，蔬菜平均每 $10$ 亩需 $3$ 人管理，茶叶平均每 $10$ 亩需 $5$ 人管理．若今年新增的管理蔬菜和茶叶的人数比为 $1$ ： $1$ ，问该农业基地管理蔬菜和茶叶今年共需新增多少人？

查看试题解析
14. 某工厂承接了一批纸箱加工任务，用如图 $1$ 所示的长方形和正方形纸板 $($ 长方形的宽与正方形的边长相等 $)$ 加工成如图所示的竖式与横式两种无盖的长方形纸箱（加工时接缝材料不计）

(1)、若该厂购进正方形纸板 $1000$ 张，长方形纸板 $2000$ 张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；

(2)、该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板 $80$ 张，长方形纸板 $a$ 张，全部加工成上述两种纸盒，且 $150 < a < 171$ ，试求在这一天加工两种纸盒时， $a$ 的所有可能值．

查看试题解析
15. 定义：在平面直角坐标系xOy中，若点 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2})$ ， $C (x_{3} ， y_{3})$ 的横坐标 $x$ 值与纵坐标 $y$ 值的有序实数对，都是方程 $a x + b y + c = 0$ 的解，则称 $A (x_{1} ， y_{1}) ， B (x_{2} ， y_{2}) ， C (x_{3} ， y_{3})$ 三点共线.(如：点 $P (2 ， 3)$ 的横坐标 $x = 2$ 与纵坐标 $y = 3$ 的有序实数对为 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是方程 $3 x - 4 y + 6 = 0$ 的解.)

(1)、已知方程 $2 x - 3 y + 5 = 0$ ，判断A、B、C、D四个点中哪三个点共线？ $A (- 1 ， 1) ， B (2 ， 3) ， C (0 ， - \frac{5}{3}) ， D (1 ， \frac{7}{3})$ .请写出判断过程.

(2)、已知方程 $(a - 1) x + 2 y + a = 0$ ，
①对于任意实数 $a$ 的值该方程总有一个固定的解，请求出固定的解；
②以①的解中 $x$ 值为点 $M$ 的横坐标， $y$ 值为点 $M$ 的纵坐标，若点 $N (2 ， t + 1)$ ， $P (3 ， 2 - t)$ 与点 $M$ 三点共线，求 $a$ 与 $t$ 的值.

查看试题解析

【培优卷】2024年浙教版数学七年级下册2.4二元一次方程组的应用 同步练习

一、选择题

二、填空题

三、解答题

【培优卷】2024年浙教版数学七年级下册2.4二元一次方程组的应用同步练习