高中数学三轮复习(直击痛点):专题16立体几何中范围和最值问题
试卷更新日期:2024-02-23 类型:三轮冲刺
一、选择题
-
1. 如图,棱长为3的正方体ABCD-A1B1C1D1中,P为正方体表面BCC1B1上的一个动点,E , F分别为BD1的三等分点,则的最小值为( )A、 B、 C、 D、2. 已知平面上两定点、 , 则所有满足(且)的点的轨迹是一个圆心在上,半径为的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称作阿氏圆.已知棱长为3的正方体表面上动点满足 , 则点的轨迹长度为( )A、 B、 C、 D、3. 如图,在直四棱柱中, , , , E , F分别是侧棱 , 上的动点,且平面与平面所成角的大小为 , 则线段的长的最大值为( )
 A、 B、 C、 D、4. 如图, 二面角的平面角的大小为为半平面内的两个点, 为半平面内一点, 且 , 若直线与平面所成角为为的中点, 则线段长度的最大值是( )
A、 B、 C、 D、4. 如图, 二面角的平面角的大小为为半平面内的两个点, 为半平面内一点, 且 , 若直线与平面所成角为为的中点, 则线段长度的最大值是( ) A、 B、 C、 D、5. 传说古希腊数学家阿基米德的募碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,为圆柱上下底面的圆心,为球心,为底面圆的一条直径,若球的半径 , 则( )
A、 B、 C、 D、5. 传说古希腊数学家阿基米德的募碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,为圆柱上下底面的圆心,为球心,为底面圆的一条直径,若球的半径 , 则( ) A、球与圆柱的表面积之比为 B、平面截得球的截面面积取值范围为 C、四面体的体积的最大值为16 D、若为球面和圆柱侧面的交线上一点,则的取值范围6. 已知 , , , 是表面积为的球面上四点, , , , 三棱锥的体积为 , 则线段长度的取值范围为( )A、 B、 C、 D、7. 已知四棱锥外接球表面积为 , 体积为平面 , 且 , 则的取值范围是( )A、 B、 C、 D、8. 平面直角坐标系中,若两点 , 满足或 , 则称点S和点T保持了合理间距.正方形中,顶点 , 动点P,Q都在正方形内(包括边界),且点P在抛物线上,则下列说法错误的是( )A、若点P与点O,A,B都保持了合理间距,则点P的横坐标的取值范围是 B、若点Q与点O,A,B都保持了合理间距,则点Q的轨迹所形成的面积为6 C、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最大值为6 D、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最小值为
A、球与圆柱的表面积之比为 B、平面截得球的截面面积取值范围为 C、四面体的体积的最大值为16 D、若为球面和圆柱侧面的交线上一点,则的取值范围6. 已知 , , , 是表面积为的球面上四点, , , , 三棱锥的体积为 , 则线段长度的取值范围为( )A、 B、 C、 D、7. 已知四棱锥外接球表面积为 , 体积为平面 , 且 , 则的取值范围是( )A、 B、 C、 D、8. 平面直角坐标系中,若两点 , 满足或 , 则称点S和点T保持了合理间距.正方形中,顶点 , 动点P,Q都在正方形内(包括边界),且点P在抛物线上,则下列说法错误的是( )A、若点P与点O,A,B都保持了合理间距,则点P的横坐标的取值范围是 B、若点Q与点O,A,B都保持了合理间距,则点Q的轨迹所形成的面积为6 C、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最大值为6 D、若点Q与点P,O,A,B都保持了合理间距,则点Q的轨迹所形成的面积最小值为二、多项选择题
-
9. 如图,在棱长为2的正方体中,E是线段的中点,点M,N满足 , 其中 , 则( )
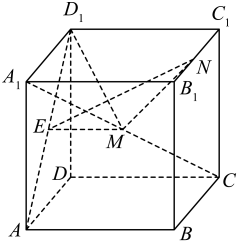 A、存在 , 使得 B、的最小值为 C、当时,直线与平面所成角的正弦值为 D、当时,过E,M,N三点的平面截正方体得到的截面多边形面积为10. 如图,棱长为6的正方体中,点、满足 , , 其中、 , 点是正方体表面上一动点,下列说法正确的是( )
A、存在 , 使得 B、的最小值为 C、当时,直线与平面所成角的正弦值为 D、当时,过E,M,N三点的平面截正方体得到的截面多边形面积为10. 如图,棱长为6的正方体中,点、满足 , , 其中、 , 点是正方体表面上一动点,下列说法正确的是( ) A、当时,∥平面 B、当时,若∥平面 , 则的最大值为 C、当时,若 , 则点的轨迹长度为 D、过A、、三点作正方体的截面,截面图形可以为矩形11. 如图,在四棱锥中,底面是边长为1的正方形.底面 , , 点是棱PB上一点(不包括端点).F是平面内一点,则( )
A、当时,∥平面 B、当时,若∥平面 , 则的最大值为 C、当时,若 , 则点的轨迹长度为 D、过A、、三点作正方体的截面,截面图形可以为矩形11. 如图,在四棱锥中,底面是边长为1的正方形.底面 , , 点是棱PB上一点(不包括端点).F是平面内一点,则( ) A、存在点 , 使平面 B、存在点 , 使平面 C、的最小值为 D、以为球心,半径为1的球与四棱锥的四个侧面的交线长为12. 已知正三棱柱的棱长均为2,点D是棱上(不含端点)的一个动点.则下列结论正确的是( )A、棱上总存在点E,使得直线平面 B、的周长有最小值,但无最大值 C、三棱锥外接球的表面积的取值范围是 D、当点D是棱的中点时,二面角的正切值为13. 已知长方体的表面积为10,十二条棱长度之和为16,则该长方体( )A、一定不是正方体 B、外接球的表面积为 C、长、宽、高的值均属于区间 D、体积的取值范围为14. 如图,在边长为2的正方形AP1P2P3中,线段BC的端点B,C分别在边P1P2 , P2P3上滑动,且P2B=P2C=x。现将△AP1B,△AP3C分别沿AB,CA折起使点P1 , P3重合,重合后记为点P,得到三棱锥P-ABC。现有以下结论:( )
A、存在点 , 使平面 B、存在点 , 使平面 C、的最小值为 D、以为球心,半径为1的球与四棱锥的四个侧面的交线长为12. 已知正三棱柱的棱长均为2,点D是棱上(不含端点)的一个动点.则下列结论正确的是( )A、棱上总存在点E,使得直线平面 B、的周长有最小值,但无最大值 C、三棱锥外接球的表面积的取值范围是 D、当点D是棱的中点时,二面角的正切值为13. 已知长方体的表面积为10,十二条棱长度之和为16,则该长方体( )A、一定不是正方体 B、外接球的表面积为 C、长、宽、高的值均属于区间 D、体积的取值范围为14. 如图,在边长为2的正方形AP1P2P3中,线段BC的端点B,C分别在边P1P2 , P2P3上滑动,且P2B=P2C=x。现将△AP1B,△AP3C分别沿AB,CA折起使点P1 , P3重合,重合后记为点P,得到三棱锥P-ABC。现有以下结论:( ) A、AP⊥平面PBC B、当B,C分别为P1P2 , P2P3的中点时,三棱锥P-ABC的外接球的表面积为6π C、x的取值范围为(0,4-2) D、三棱锥P-ABC体积的最大值为15. 如图圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等, , 为圆柱上下底面的圆心,O为球心,EF为底面圆的一条直径,若球的半径 , 则( )
A、AP⊥平面PBC B、当B,C分别为P1P2 , P2P3的中点时,三棱锥P-ABC的外接球的表面积为6π C、x的取值范围为(0,4-2) D、三棱锥P-ABC体积的最大值为15. 如图圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等, , 为圆柱上下底面的圆心,O为球心,EF为底面圆的一条直径,若球的半径 , 则( ) A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为16. 如图,圆锥内有一个内切球 , 球与母线分别切于点.若是边长为2的等边三角形,为圆锥底面圆的中心,为圆的一条直径(与不重合),则下列说法正确的是( )
A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为16. 如图,圆锥内有一个内切球 , 球与母线分别切于点.若是边长为2的等边三角形,为圆锥底面圆的中心,为圆的一条直径(与不重合),则下列说法正确的是( ) A、球的表面积与圆锥的侧面积之比为 B、平面截得圆锥侧面的交线形状为抛物线 C、四面体的体积的取值范围是 D、若为球面和圆锥侧面的交线上一点,则最大值为17. 很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体.如图,这是一个棱数为24,棱长为的半正多面体,它的所有顶点都在同一个正方体的表面上,可以看成是由一个正方体截去八个一样的四面体所得,则下列各选项正确的是( )
A、球的表面积与圆锥的侧面积之比为 B、平面截得圆锥侧面的交线形状为抛物线 C、四面体的体积的取值范围是 D、若为球面和圆锥侧面的交线上一点,则最大值为17. 很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体.如图,这是一个棱数为24,棱长为的半正多面体,它的所有顶点都在同一个正方体的表面上,可以看成是由一个正方体截去八个一样的四面体所得,则下列各选项正确的是( )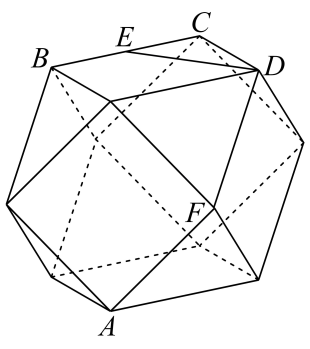 A、该半正多面体的体积为 B、A,C,D,F四点共面 C、该半正多面体外接球的表面积为 D、若点E为线段BC上的动点,则直线DE与直线AF所成角的余弦值的取值范围为18. 已知三棱锥D-ABC的外接球的表面积为24π,直角三角形ABC的斜边 , CD⊥BC,则( )A、BC⊥平面ACD B、点D的轨迹的长度为2π C、线段CD长的取值范围为(0,2] D、三棱锥D-ABC体积的最大值为19. 如图,圆锥的底面圆的直径 , 母线长为 , 点是圆上异于 , 的动点,则下列结论正确的是( )
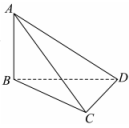
A、该半正多面体的体积为 B、A,C,D,F四点共面 C、该半正多面体外接球的表面积为 D、若点E为线段BC上的动点,则直线DE与直线AF所成角的余弦值的取值范围为18. 已知三棱锥D-ABC的外接球的表面积为24π,直角三角形ABC的斜边 , CD⊥BC,则( )A、BC⊥平面ACD B、点D的轨迹的长度为2π C、线段CD长的取值范围为(0,2] D、三棱锥D-ABC体积的最大值为19. 如图,圆锥的底面圆的直径 , 母线长为 , 点是圆上异于 , 的动点,则下列结论正确的是( ) A、与底面所成角为45° B、圆锥的表面积为 C、的取值范围是 D、若点为弧的中点,则二面角的平面角大小为45°20. 在边长为4的正方形ABCD中,如图1所示,E,F,M分别为BC,CD,BE的中点,分别沿AE,AF及EF所在直线把 , 和 折起,使B,C,D三点重合于点P,得到三棱锥 ,如图2所示,则下列结论中正确的是( )
A、与底面所成角为45° B、圆锥的表面积为 C、的取值范围是 D、若点为弧的中点,则二面角的平面角大小为45°20. 在边长为4的正方形ABCD中,如图1所示,E,F,M分别为BC,CD,BE的中点,分别沿AE,AF及EF所在直线把 , 和 折起,使B,C,D三点重合于点P,得到三棱锥 ,如图2所示,则下列结论中正确的是( ) A、 B、三棱锥 的体积为4 C、三棱锥 外接球的表面积为 D、过点M的平面截三棱锥 的外接球所得截面的面积的取值范围为
A、 B、三棱锥 的体积为4 C、三棱锥 外接球的表面积为 D、过点M的平面截三棱锥 的外接球所得截面的面积的取值范围为三、填空题
-
21. 已知正方体的棱长为2,点M是棱BC的中点.(1)、若点N为棱的中点,则平面AMN截正方体的截面的面积为;(2)、若点N是棱上的一个动点,则点到平面AMN的距离的最小值为.22. 若正四面体的棱长为3,平面ABC内有一动点P到平面、平面、平面的距离依次成等差数列,则点P在面内的轨迹的长度为.23. 已知正方体的棱长为3,动点在平面内,且AP与所成角为 , 则长度的最小值为.24. 已知正四面体的外接球半径为3,MN为其外接球的一条直径,P为正四面体表面上任意一点,则的最小值为 .25. 在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑中,平面 , 已知动点从点出发,沿外表面经过棱上一点到点的最短距离为 , 则该棱锥的外接球的体积为 .
 26. 已知矩形 , 设E是边上的一点,且 . 现将沿着直线翻折至 , 设二面角的大小为 , 则的最大值是 .27. 如图,四棱锥中,平面平面 , 底面是边长为2的正方形,是等腰三角形,则平面上任意一点到底面中心距离的最小值为.
26. 已知矩形 , 设E是边上的一点,且 . 现将沿着直线翻折至 , 设二面角的大小为 , 则的最大值是 .27. 如图,四棱锥中,平面平面 , 底面是边长为2的正方形,是等腰三角形,则平面上任意一点到底面中心距离的最小值为. 28. 如图,正四棱台 , 上下底面分别是边长为4,6的正方形,若 , 则该棱台外接球表面积的取值范围是 .
28. 如图,正四棱台 , 上下底面分别是边长为4,6的正方形,若 , 则该棱台外接球表面积的取值范围是 .
四、解答题
-
29. 如图,菱形的边长为2, , E为AB的中点.将沿DE折起,使A到达 , 连接 , , 得到四棱锥 .
 (1)、证明:;(2)、当二面角的平面角在内变化时,求直线与平面所成角的正弦值的取值范围.30. 如图,点在内,是三棱锥的高,且 . 是边长为的正三角形, , 为中点.
(1)、证明:;(2)、当二面角的平面角在内变化时,求直线与平面所成角的正弦值的取值范围.30. 如图,点在内,是三棱锥的高,且 . 是边长为的正三角形, , 为中点. (1)、证明:点在上.(2)、点是棱上的一点(不含端点),求平面与平面夹角余弦值的最大值.
(1)、证明:点在上.(2)、点是棱上的一点(不含端点),求平面与平面夹角余弦值的最大值.
