高中数学三轮复习(直击痛点):专题14截面问题
试卷更新日期:2024-02-23 类型:三轮冲刺
一、选择题
-
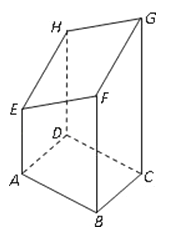
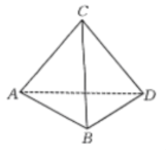
1. 已知四棱锥中,平面 , 四边形为正方形, , 平面过 , , 的中点,则下列关于平面截四棱锥所得的截面正确的为( )A、所得截面是正五边形 B、截面过棱的三等分点 C、所得截面面积为 D、截面不经过中点2. 下列叙述正确的是( )A、用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台 B、两个面平行且相似,其余各面都是梯形的多面体是棱台 C、有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台 D、棱台的侧棱延长后必交于一点3. 一正四面体木块如图所示,点 是棱 的中点,过点P将木块锯开,使截面平行于棱 和 ,则下列关于截面的说法正确的是( ).
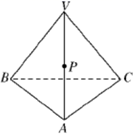 A、满足条件的截面不存在 B、截面是一个梯形 C、截面是一个菱形 D、截面是一个三角形4. 在正方体中,为棱的一个三等分点(靠近点),分别为棱 , 的中点,过三点作正方体的截面,则下列说法正确的是( )
A、满足条件的截面不存在 B、截面是一个梯形 C、截面是一个菱形 D、截面是一个三角形4. 在正方体中,为棱的一个三等分点(靠近点),分别为棱 , 的中点,过三点作正方体的截面,则下列说法正确的是( )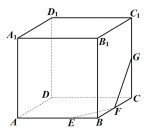 A、所得截面是六边形 B、截面过棱的中点 C、截面不经过点 D、截面与线段相交,且交点是线段的一个五等分点5. 已知过的平面与正方体相交,分别交棱 , 于 , .则下列关于截面的说法中,不正确的是( )
A、所得截面是六边形 B、截面过棱的中点 C、截面不经过点 D、截面与线段相交,且交点是线段的一个五等分点5. 已知过的平面与正方体相交,分别交棱 , 于 , .则下列关于截面的说法中,不正确的是( )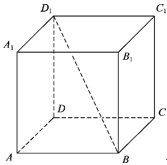 A、截面可能是矩形 B、截面可能是菱形 C、截面可能是梯形 D、截面不可能是正方形
A、截面可能是矩形 B、截面可能是菱形 C、截面可能是梯形 D、截面不可能是正方形二、多项选择题
-
6. 如图,有一个正四面体形状的木块,其棱长为.现准备将该木块锯开,则下列关于截面的说法中正确的是( )
 A、过棱的截面中,截面面积的最小值为 B、若过棱的截面与棱(不含端点)交于点 , 则 C、若该木块的截面为平行四边形,则该截面面积的最大值为 D、与该木块各个顶点的距离都相等的截面有7个7. 如图,已知正方体的棱长为1,E为的中点,P为对角线上的一个动点,过P作与平面ACE平行的平面,则此平面截正方体所得的截面( )
A、过棱的截面中,截面面积的最小值为 B、若过棱的截面与棱(不含端点)交于点 , 则 C、若该木块的截面为平行四边形,则该截面面积的最大值为 D、与该木块各个顶点的距离都相等的截面有7个7. 如图,已知正方体的棱长为1,E为的中点,P为对角线上的一个动点,过P作与平面ACE平行的平面,则此平面截正方体所得的截面( )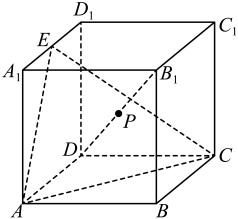 A、截面不可能是五边形 B、截面可以是正六边形 C、P从D点向运动时,截面面积先增大后减小 D、截面面积的最大值为8. 已知棱长为2的正方体的中心为 , 用过点的平面去截正方体,则( )A、所得的截面可以是五边形 B、所得的截面可以是六边形 C、该截面的面积可以为 D、所得的截面可以是非正方形的菱形9. 已知正方体的棱长为2,过棱 , 的中点E,F作正方体的截面,下列说法正确的是( ).A、该正方体外接球的表面积是 B、若截面是正六边形,则直线与截面垂直 C、若截面是正六边形,则直线与截面所成角的正弦值为 D、若截面过点,则截面周长为10. 数学中有许多形状优美、寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体ABCD的棱长为4,则下列结论正确的是( )
A、截面不可能是五边形 B、截面可以是正六边形 C、P从D点向运动时,截面面积先增大后减小 D、截面面积的最大值为8. 已知棱长为2的正方体的中心为 , 用过点的平面去截正方体,则( )A、所得的截面可以是五边形 B、所得的截面可以是六边形 C、该截面的面积可以为 D、所得的截面可以是非正方形的菱形9. 已知正方体的棱长为2,过棱 , 的中点E,F作正方体的截面,下列说法正确的是( ).A、该正方体外接球的表面积是 B、若截面是正六边形,则直线与截面垂直 C、若截面是正六边形,则直线与截面所成角的正弦值为 D、若截面过点,则截面周长为10. 数学中有许多形状优美、寓意独特的几何体,“勒洛四面体”就是其中之一.勒洛四面体是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体中,正四面体ABCD的棱长为4,则下列结论正确的是( )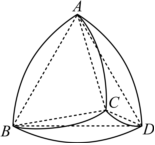 A、勒洛四面体ABCD最大的截面是正三角形 B、勒洛四面体ABCD的体积大于正四面体ABCD的体积 C、勒洛四面体ABCD被平面ABC截得的截面面积是 D、勒洛四面体ABCD四个曲面所有交线长的和为8π11. 在正方体中,E,F分别为AB,BC的中点,G为线段上的动点,过E,F,G作正方体的截面记为 , 则( )
A、勒洛四面体ABCD最大的截面是正三角形 B、勒洛四面体ABCD的体积大于正四面体ABCD的体积 C、勒洛四面体ABCD被平面ABC截得的截面面积是 D、勒洛四面体ABCD四个曲面所有交线长的和为8π11. 在正方体中,E,F分别为AB,BC的中点,G为线段上的动点,过E,F,G作正方体的截面记为 , 则( )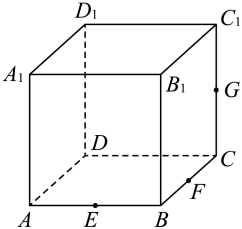 A、当截面为正六边形时,G为中点 B、当时,截面为五边形 C、截面可能是等腰梯形 D、截面不可能与直线垂直12. 棱长为1的正方体中,P、Q分别在棱BC、上, , , , 且 , 过A、P、Q三点的平面截正方体得到截面多边形,则( )
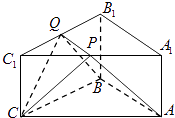
A、当截面为正六边形时,G为中点 B、当时,截面为五边形 C、截面可能是等腰梯形 D、截面不可能与直线垂直12. 棱长为1的正方体中,P、Q分别在棱BC、上, , , , 且 , 过A、P、Q三点的平面截正方体得到截面多边形,则( )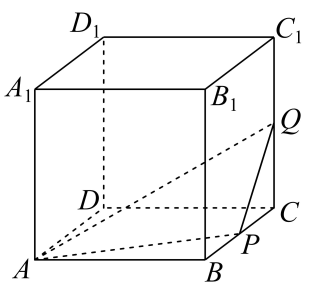 A、时,截面一定为等腰梯形 B、时,截面一定为矩形且面积最大值为 C、存在x,y使截面为六边形 D、存在x,y使与截面平行13. 正方体 的棱长为2,用一个平面 截这个正方体,把该正方体分为体积相等的两部分,则下列结论正确的是( )A、这两部分的表面积也相等 B、截面可以是三角形 C、截面可以是五边形 D、截面可以是正六边形14. 截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图所示,将棱长为3的正四面体沿棱的三等分点做平行于底面的截面得到的所有棱长均为1的截角四面体,则下列说法正确的有( )
A、时,截面一定为等腰梯形 B、时,截面一定为矩形且面积最大值为 C、存在x,y使截面为六边形 D、存在x,y使与截面平行13. 正方体 的棱长为2,用一个平面 截这个正方体,把该正方体分为体积相等的两部分,则下列结论正确的是( )A、这两部分的表面积也相等 B、截面可以是三角形 C、截面可以是五边形 D、截面可以是正六边形14. 截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图所示,将棱长为3的正四面体沿棱的三等分点做平行于底面的截面得到的所有棱长均为1的截角四面体,则下列说法正确的有( )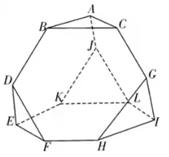 A、该截角四面体的表面积为 B、该截角四面体的体积为 C、该截角四面体中,GH∥JK D、二面角 B-AC-D的余弦值为15. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,已知M,N,P分别是棱C1D1 , AA1 , BC的中点,Q为平面PMN上的动点,且直线QB1与直线DB1的夹角为30°,则( )
A、该截角四面体的表面积为 B、该截角四面体的体积为 C、该截角四面体中,GH∥JK D、二面角 B-AC-D的余弦值为15. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,已知M,N,P分别是棱C1D1 , AA1 , BC的中点,Q为平面PMN上的动点,且直线QB1与直线DB1的夹角为30°,则( )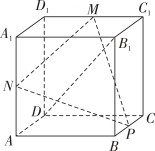 A、DB1⊥平面PMN B、平面PMN截正方体所得的截面面积为3 C、点Q的轨迹长度为π D、能放入由平面PMN分割该正方体所成的两个空间几何体内部(厚度忽略不计)的球的半径的最大值为16. 如图,棱长为2的正四面体中,分别为棱的中点,O为线段的中点,球O的表面正好经过点M,则下列结论中正确的是( )
A、DB1⊥平面PMN B、平面PMN截正方体所得的截面面积为3 C、点Q的轨迹长度为π D、能放入由平面PMN分割该正方体所成的两个空间几何体内部(厚度忽略不计)的球的半径的最大值为16. 如图,棱长为2的正四面体中,分别为棱的中点,O为线段的中点,球O的表面正好经过点M,则下列结论中正确的是( )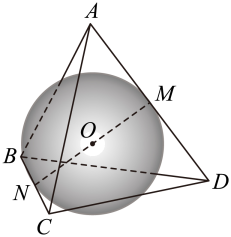 A、平面 B、球O的体积为 C、球O被平面截得的截面面积为 D、球O被正四面体表面截得的截面周长为17. 如图,在棱长为2的正方体中,E是棱的中点,过作正方体的截面交棱于F,则( )
A、平面 B、球O的体积为 C、球O被平面截得的截面面积为 D、球O被正四面体表面截得的截面周长为17. 如图,在棱长为2的正方体中,E是棱的中点,过作正方体的截面交棱于F,则( )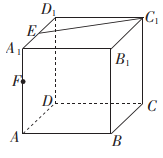 A、当时,截面为等腰梯形 B、当时,截面为六边形 C、当时,截面面积为2 D、当时,截面与平面所成的锐二面角的正切值为
A、当时,截面为等腰梯形 B、当时,截面为六边形 C、当时,截面面积为2 D、当时,截面与平面所成的锐二面角的正切值为三、填空题
-
18. 已知球的两个平行截面的面积分别为 , 且两个截面之间的距离是 , 则球的表面积为 .19. 在棱长为6的正方体中,E是棱AB的中点,过作正方体的截面,则该截面的面积是 .20. 一个正四面体木块如图所示,点是棱的中点.过点将木块锯开,使截面平行于棱和 , 若木块的棱长为 , 则截面面积为
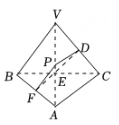 21. 如图,三棱锥的三条侧棱两两垂直,且 . 点是侧面内一点,过点作一个既平行于侧棱 , 又平行于底边的三棱锥的截面,则该截面面积的最大值为 .
21. 如图,三棱锥的三条侧棱两两垂直,且 . 点是侧面内一点,过点作一个既平行于侧棱 , 又平行于底边的三棱锥的截面,则该截面面积的最大值为 .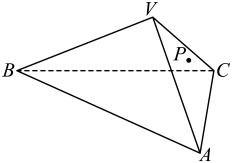 22. 某学习小组研究一种如图1所示的卫星接收天线,发现其轴截面为图2所示的抛物线形,在轴截面内的卫星信号波束呈近似平行的状态射入,经反射聚焦到焦点处,已知卫星接收天线的口径(直径)为 , 深度为 , 则该卫星接收天线轴截面所在的抛物线的焦点到顶点的距离为.
22. 某学习小组研究一种如图1所示的卫星接收天线,发现其轴截面为图2所示的抛物线形,在轴截面内的卫星信号波束呈近似平行的状态射入,经反射聚焦到焦点处,已知卫星接收天线的口径(直径)为 , 深度为 , 则该卫星接收天线轴截面所在的抛物线的焦点到顶点的距离为. 23. 如图,正方体的棱长为 , 点是棱的中点,过的平面与平面平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为 .
23. 如图,正方体的棱长为 , 点是棱的中点,过的平面与平面平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为 .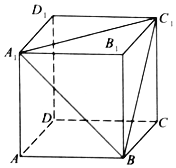 24. 在正四面体中,为边的中点,过点作该正四面体外接球的截面,记最大的截面面积 , 最小的截面面积为 , 则;若记该正四面体内切球和外接球的体积分别为和 , 则 .25. 已知圆锥的轴截面是边长为的等边三角形,则圆锥的体积为 .
24. 在正四面体中,为边的中点,过点作该正四面体外接球的截面,记最大的截面面积 , 最小的截面面积为 , 则;若记该正四面体内切球和外接球的体积分别为和 , 则 .25. 已知圆锥的轴截面是边长为的等边三角形,则圆锥的体积为 .四、解答题
-
26. 如图,在正三棱台中, , , 过棱的截面与棱 , 分别交于、.
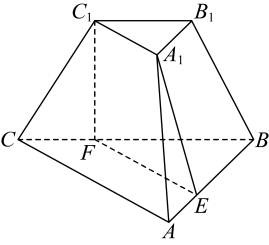 (1)、记几何体和正三棱台
(1)、记几何体和正三棱台 体积分别为 , , 若 , 求的长度; (2)、若 , 求直线与平面所成角的正弦值.27. 已知正方体中,点E,F分别是棱 , 的中点,过点作出正方体的截面,使得该截面平行于平面 .
体积分别为 , , 若 , 求的长度; (2)、若 , 求直线与平面所成角的正弦值.27. 已知正方体中,点E,F分别是棱 , 的中点,过点作出正方体的截面,使得该截面平行于平面 .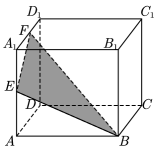 (1)、作出该截面与正方体表面的交线,并说明理由;(2)、求与该截面所在平面所成角的正弦值.
(1)、作出该截面与正方体表面的交线,并说明理由;(2)、求与该截面所在平面所成角的正弦值.(截面:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.)
28. 广州塔外形优美,游客都亲切地称之为“小蛮腰”,其主塔部分可近似地看成是由一个双曲面和上下两个圆面围成的.其中双曲面的构成原理如图所示:圆 , 所在的平面平行,垂直于圆面,AB为一条长度为定值的线段,其端点A,B分别在圆 , 上,当A,B在圆上运动时,线段AB形成的轨迹曲面就是双曲面.用过的任意一个平面去截双曲面得到的截面曲线都是双曲线,我们称之为截面双曲线.已知主塔的高度 , , 设塔身最细处的圆的半径为 , 上、下圆面的半径分别为、 , 且 , , 成公比为的等比数列.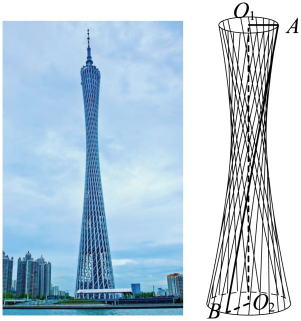 (1)、求与的夹角;(2)、建立适当的坐标系,求该双曲面的截面双曲线的渐近线方程.29. 在水平桌面上放一只内壁光滑的玻璃水杯,已知水杯内壁为抛物面型(抛物面指抛物线绕其对称轴旋转所得到的面),抛物面的轴截面是如图所示的抛物线.现有一些长短不一、质地均匀的细直金属棒,其长度均不小于抛物线通径的长度(通径是过抛物线焦点,且与抛物线的对称轴垂直的直线被抛物线截得的弦),若将这些细直金属棒,随意丢入该水杯中,实验发现:当细棒重心最低时,达到静止状态,此时细棒交汇于一点.
(1)、求与的夹角;(2)、建立适当的坐标系,求该双曲面的截面双曲线的渐近线方程.29. 在水平桌面上放一只内壁光滑的玻璃水杯,已知水杯内壁为抛物面型(抛物面指抛物线绕其对称轴旋转所得到的面),抛物面的轴截面是如图所示的抛物线.现有一些长短不一、质地均匀的细直金属棒,其长度均不小于抛物线通径的长度(通径是过抛物线焦点,且与抛物线的对称轴垂直的直线被抛物线截得的弦),若将这些细直金属棒,随意丢入该水杯中,实验发现:当细棒重心最低时,达到静止状态,此时细棒交汇于一点.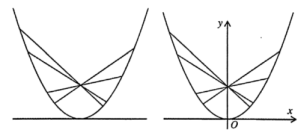 (1)、请结合你学过的数学知识,猜想细棒交汇点的位置;(2)、以玻璃水杯内壁轴截面的抛物线顶点为原点,建立如图所示直角坐标系.设玻璃水杯内壁轴截面的抛物线方程为 , 将细直金属棒视为抛物线的弦 , 且弦长度为 , 以细直金属棒的中点为其重心,请从数学角度解释上述实验现象.30. 2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
(1)、请结合你学过的数学知识,猜想细棒交汇点的位置;(2)、以玻璃水杯内壁轴截面的抛物线顶点为原点,建立如图所示直角坐标系.设玻璃水杯内壁轴截面的抛物线方程为 , 将细直金属棒视为抛物线的弦 , 且弦长度为 , 以细直金属棒的中点为其重心,请从数学角度解释上述实验现象.30. 2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.
(Ⅰ)利用祖暅原理推导半径为 的球的体积公式时,可以构造如图②所示的几何体 ,几何体 的底面半径和高都为 ,其底面和半球体的底面同在平面 内.设与平面 平行且距离为 的平面 截两个几何体得到两个截面,请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明;
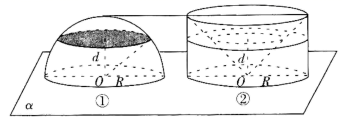
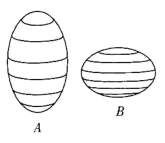
(Ⅱ)现将椭圆 所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球 , (如图),类比(Ⅰ)中的方法,探究椭球 的体积公式,并写出椭球 , 的体积之比.
 31. 已知三棱锥S﹣ABC,SC∥截面EFGH,AB∥截面EFGH.求证:截面EFGH是平行四边形.32. 如图所示,在棱长为2cm的正方体ABCD﹣A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
31. 已知三棱锥S﹣ABC,SC∥截面EFGH,AB∥截面EFGH.求证:截面EFGH是平行四边形.32. 如图所示,在棱长为2cm的正方体ABCD﹣A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.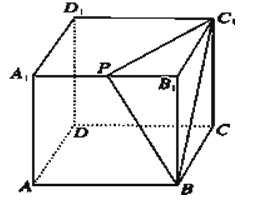 33. 球的两个平行截面的面积分别为5π,8π两截面之间的距离为1,求球的半径.
33. 球的两个平行截面的面积分别为5π,8π两截面之间的距离为1,求球的半径. 34. 如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
34. 如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.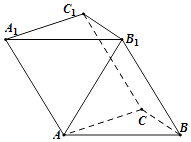
(Ⅰ)过B1作出三棱柱的截面,使截面垂直于AB,并证明;
(Ⅱ)求AC1与平面BCC1B1所成角的正弦值.
35. 已知正三棱锥S﹣ABC的高SO=h,斜高SM=n,求经过SO的中点且平行于底面的截面△A1B1C1的面积.36. 已知:正方体ABCD-A1B1C1D1 , 如图,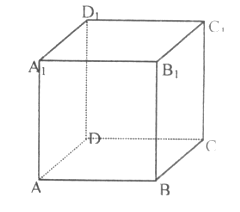
(Ⅰ)若E、F为AA1、CC1的中点,画出过D1、E、F的截面;
(Ⅱ)若M、N、P为A1B1、BB1、B1C1上的点(均不与B1重合),求证:△MNP是锐角三角形。