（华师大版）2023-2024学年度第二学期八年级数学20.3 数据的离散程度 同步测试
试卷更新日期：2024-02-22 类型：同步测试
一、选择题
-
1. 某射击运动员在训练中射击了10次，成绩如图所示：
某射击运动员在训练中射击环数折线统计图
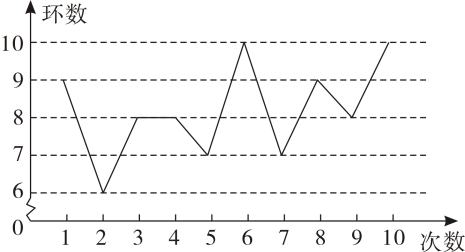
下列结论中，错误的是 （ ）
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是 1.22. 一组数据2，3，4，5，6的方差是 （ ）A、 B、2 C、4 D、53. 方差是刻画数据波动程度的量，对于一组数据x1 ， x2 ， x3 ， …，xn ， 可用如下算式计算方差： S²= ， 其中“5”是这组数据的 （ ）A、最小值 B、平均数 C、中位数 D、和4. 在5轮“汉字听写大赛”选拔赛中，甲、乙两位同学的平均分都是90分，甲的成绩的方差是15，乙的成绩的方差是3，下列说法中，正确的是 （ ）A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定5. 小莹同学10周的综合素质评价成绩统计如下表所示：成绩(分)
94
95
97
98
100
周数
1
2
2
4
1
这10周的综合素质评价成绩的中位数和方差分别是 （ ）
A、97.5分，2.8分² B、97.5分，3分² C、97分，2.8分² D、97分，3分²6. 已知一组数据的方差是3，则这组数据的标准差是（ ）A、3 B、± C、 D、7. A，B两名射击运动员进行了相同次数的射击，下列关于他们射击成绩的平均数和方差的描述中，能说明A成绩较好且更稳定的是（ ）A、>且> B、<且> C、>且< D、<且<8. 用计算器计算方差时，要首先进入统计计算状态，需要按键（ ）A、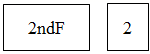
B、
C、
D、
9. 在新型冠状病毒防控期间，小静坚持每天测量自己的体温，并把5次的体温（单位： ）分别写在5张完全相同的卡片上：36，36.1，35.9，35.5，背面，把这5张卡片背面朝上洗匀后，从中随机抽取一张卡片，已知P（一次抽到36） ，这5张卡片上数据的方差为（ ）A、35.9 B、0.22 C、0.044 D、010. 已知一组数据70，29，71，72，81，73，105，69，用计算器求得这组数据的方差为（精确到0.01）（ ）.A、378 B、377.69 C、378.70 D、378.69二、填空题
-
11. 已知一组数据的方差计算如下： ， 则这组数据的和是12. 教练对跳远运动员小刚的训练效果进行了测试，6次跳远的成绩(单位：m)如下：7.6，7.8，7.7，7.8，8.0，7.9.这6次成绩的平均数是7.8m，方差是 m².若小刚再跳两次，成绩分别是7.7，7.9，则小刚这8次跳远成绩的方差将(填“变大”“变小”或“不变”).13. 已知一组数据x₁，x₂，x₃，…，x。的方差是 1.5，则另一组 数 据 2x₁，2x₂， 2x₃，…，2x， 的方差是.14. 利用计算器求标准差和方差时，首先要进入计算状态，再依次输入每一个数据，最后按求方差的功能键 ， 即可得出结果．15. 甲、乙两班举行数学知识竞赛，参赛学生的竞赛得分统计分析结果如下表所示：
班级
参赛人数
平均数(分)
中位数(分)
方差(分²)
甲
45
83
86
82
乙
45
83
84
135
某同学分析上表后得到如下结论：
①甲、乙两班学生的平均成绩相同；
②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀)；
③甲班成绩比乙班稳定.
上述结论中，正确的是(填序号).
三、解答题
-
16. 某班为了从李明、张亮两名男同学中选拔一人参加全校举行的1分钟跳绳比赛，现对他们进行了训练测试，他们 10次测试的成绩如下(单位：次)：
李明：186，191，196，191，186，201，196，196，211，206；
张亮：171，186，182，191，201，197，201，205，211，215.
为了比较两人的成绩，制作了统计分析表：
平均数 中位数 众数 方差 李明 196 196 a C 张亮 196 b 201 166.4 (1)、填空：a=.b=.(2)、求出李明成绩的方差.(3)、以中位数或方差作为选拔标准，说明应选拔哪一位同学参加全校举行的跳绳比赛.17. 某校组织学生参加“用电安全知识竞赛" ，为了解竞赛情况，从两个年级各抽取10名学生的成绩(满分为100分)．收集数据：
七年级：90 ，95 ，95 ，80，85 ，90， 80，90， 85，100；
八年级：85 ，85 ，95 ，80 ，95 ，90 ，90 ，90，100，90．
分析数据：
平均数
中位数
众数
方差
七年级
89
m
90
39
八年级
n
90
p
q
根据以上信息回答下列问题：
(1)、m= ， n= ， p=.(2)、从方差的角度看，哪个年级的成绩更稳定？(3)、通过数据分析，你认为哪个年级的成绩比较好？说明理由．18. 某中学开展“迎接党的二十大”知识比赛，九年级（1）班、（2）班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如图所示．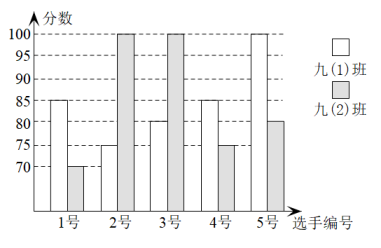
(1)、根据图示填写表格：班级
中位数
平均数
众数
九（1）班
85
？
85
九（2）班
？
85
？
(2)、结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩较好？说明理由；(3)、如果规定成绩较稳定的班级胜出，你认为哪个班级能胜出？说明理由．