华师大版数学八年级下册19.3 正方形 同步测试
试卷更新日期:2024-02-22 类型:同步测试
一、选择题
-
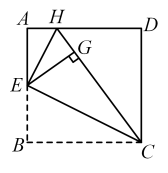
1. 如图,将正方形纸片折叠,使边均落在对角线上,得折痕 , 则的度数是( )
 A、 B、 C、 D、2. 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( )
A、 B、 C、 D、2. 如图,在边长为1的正方形ABCD中,对角线AC和BD相交于点O,P是BC边上任意一点,PE⊥BD于点E,PF⊥AC于点F,则PE+PF=( ) A、 B、 C、 D、3. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( )
A、 B、 C、 D、3. 如图,以直角三角形的三边为边向外作正方形,根据图中数据,可得出正方形A的面积是( ) A、12 B、24 C、30 D、104. 如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为 , , 有如下三个结论:
A、12 B、24 C、30 D、104. 如图,在甲、乙两个大小不同的6×6的正方形网格中,正方形ABCD,EFGH分别在两个网格上,且各顶点均在网格线的交点上.若正方形ABCD,EFGH的面积相等,甲、乙两个正方形网格的面积分别记为 , , 有如下三个结论:①正方形ABCD的面积等于的一半;②正方形EFGH的面积等于的一半;③ .

上述结论中,所有正确结论的序号是( )
A、①② B、②③ C、③ D、①②③5. 在平行四边形的复习课上,小明绘制了如下知识框架图,箭头处添加条件错误的是( ) A、①:对角线相等 B、②:对角互补 C、③:一组邻边相等 D、④:有一个角是直角6. 如图,点M是正方形ABCD内位于对角线BD下方的一点, ,则 为( )
A、①:对角线相等 B、②:对角互补 C、③:一组邻边相等 D、④:有一个角是直角6. 如图,点M是正方形ABCD内位于对角线BD下方的一点, ,则 为( )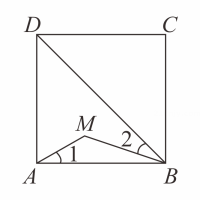 A、120° B、130° C、125° D、135°7. 若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )A、6cm B、5cm C、cm D、7.5cm8. 如图,延长正方形ABCD的一边BC到E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( )
A、120° B、130° C、125° D、135°7. 若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )A、6cm B、5cm C、cm D、7.5cm8. 如图,延长正方形ABCD的一边BC到E,使CE=AC,连接AE交CD于F,则∠AFC的度数是( ) A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°。若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°。若AB=15,则正方形ADEC和正方形BCFG的面积和为( ) A、150 B、200 C、225 D、无法计算10. 如图,F是正方形对角线上一点,连接 , , 并延长交于点E.若 , 则的度数为( )
A、150 B、200 C、225 D、无法计算10. 如图,F是正方形对角线上一点,连接 , , 并延长交于点E.若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,AC是正方形ABCD的对角线,∠DCA的平分线交BA的延长线于点E,若AB=3,则AE=
 12. 如图,在矩形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使矩形ABCD是正方形.
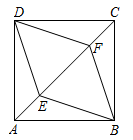
12. 如图,在矩形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使矩形ABCD是正方形. 13. 如图,两个边长为4的正方形重叠在一起,点是其中一个正方形的中心,则图中阴影部分的面积为 .
13. 如图,两个边长为4的正方形重叠在一起,点是其中一个正方形的中心,则图中阴影部分的面积为 . 14. 如图,四边形 是正方形,延长 到点 ,使 ,则 的度数是。
14. 如图,四边形 是正方形,延长 到点 ,使 ,则 的度数是。 15. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.
15. 如图,△ABC中,∠ACB =90°,AC=9,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,已知DF=4,则AD的长是.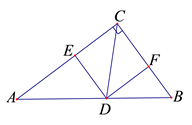
三、解答题
-
16. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点M,D分别在OA ,AB上,且AD=AM=2.一次函数y=kx+b的图象过点D和M,反比例函数y= 的图象经过点D,与BC交点为N.
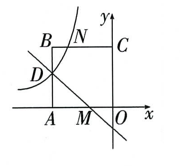 (1)、求反比例函数和一次函数的表达式;(2)、若点P在y轴上,且使四边形OMDP的面积与四边形OMNC的面积相等,求点P的坐标.17. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
(1)、求反比例函数和一次函数的表达式;(2)、若点P在y轴上,且使四边形OMDP的面积与四边形OMNC的面积相等,求点P的坐标.17. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.