(华师大版)2023-2024学年度第二学期八年级数学19.2 菱形 同步测试
试卷更新日期:2024-02-22 类型:同步测试
一、选择题
-
1. 如图,菱形ABCD的两条对角线交于点O,BE⊥DC,交DC的延长线于点E,若AC=6, BD=8,则BE的长是( )
 A、 B、 C、 D、42. 如图,四边形ABCD 是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为12和24时,阴影部分的面积为 ( )
A、 B、 C、 D、42. 如图,四边形ABCD 是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为12和24时,阴影部分的面积为 ( )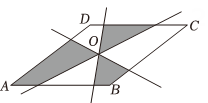 A、144 B、96 C、72 D、483. 如图,四边形ABCD的对角线相交于点O,且O是BD 的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为 ( )
A、144 B、96 C、72 D、483. 如图,四边形ABCD的对角线相交于点O,且O是BD 的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为 ( ) A、40 B、24 C、20 D、154. 如图,在菱形ABCD中,∠D=150°,则∠1=( )
A、40 B、24 C、20 D、154. 如图,在菱形ABCD中,∠D=150°,则∠1=( ) A、30° B、25° C、20° D、15°5. 如图,菱形 ABCD的对角线AC,BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为 E,则AE 的长为 ( )
A、30° B、25° C、20° D、15°5. 如图,菱形 ABCD的对角线AC,BD相交于点O.若AC=6,BD=8,AE⊥BC,垂足为 E,则AE 的长为 ( ) A、 B、 C、 D、106. 如图,将△ABC沿BC方向平移得到△DCE,连结BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
A、 B、 C、 D、106. 如图,将△ABC沿BC方向平移得到△DCE,连结BD,AD,下列条件不能判定四边形ABCD是菱形的是( )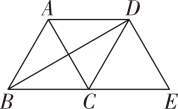 A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD7. 用直尺和圆规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )A、
A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD7. 用直尺和圆规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )A、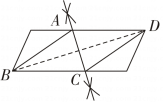 B、
B、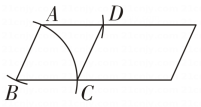 C、
C、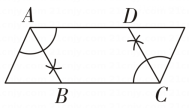 D、
D、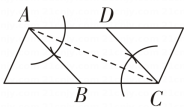 8. 如图,四边形 ABCD的对角线互相平分,要使它变为菱形,还需要添加的条件是( )
8. 如图,四边形 ABCD的对角线互相平分,要使它变为菱形,还需要添加的条件是( )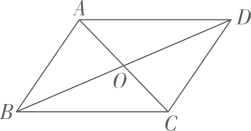 A、AB=CD B、AD=BC C、AC=BD D、AB=BC9. 如图,丝带重叠的部分一定是( )
A、AB=CD B、AD=BC C、AC=BD D、AB=BC9. 如图,丝带重叠的部分一定是( ) A、正方形 B、矩形 C、菱形 D、都有可能10. 如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )
A、正方形 B、矩形 C、菱形 D、都有可能10. 如图,剪两张对边平行的纸片随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( ) A、AB=BC B、∠DAB+∠ABC=180° C、AB=CD,AD=BC D、∠ABC=∠ADC,∠BAD=∠BCD
A、AB=BC B、∠DAB+∠ABC=180° C、AB=CD,AD=BC D、∠ABC=∠ADC,∠BAD=∠BCD二、填空题
-
11. 已知点A(0,3),B(6,0),C是x轴正半轴上一点,D是同一平面直角坐标系内一点.若以 A,B,C,D为顶点的四边形是菱形,则点 D 的坐标为.12. 如图,菱形ABCD的对角线AC,BD相交于点O,已知AC=24,BD=10,则菱形 ABCD的周长为.
 13. 如图, , , 点是射线上的任意一点,连接 , 以 , 为邻边作平行四边形 , 连 , 则线段的最小值为 .
13. 如图, , , 点是射线上的任意一点,连接 , 以 , 为邻边作平行四边形 , 连 , 则线段的最小值为 . 14. 取两根长度不等的细木条,让两个木棒的中点重合并固定在一起,用笔和直尺画出木棒四个端点的连线,当两根木棒之间的夹角等于时,得到的图形是 .15. 如图,在矩形中,对角线的垂直平分线分别交 , 于点 , , 连接 , , 如果 , 则
14. 取两根长度不等的细木条,让两个木棒的中点重合并固定在一起,用笔和直尺画出木棒四个端点的连线,当两根木棒之间的夹角等于时,得到的图形是 .15. 如图,在矩形中,对角线的垂直平分线分别交 , 于点 , , 连接 , , 如果 , 则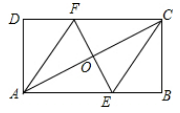
三、解答题
-
16. 如图,在▱ABCD中,AC,BD相交于点O,点E,F在AC 上,AE=CF.
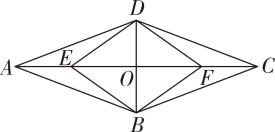 (1)、求证:四边形 EBFD是平行四边形.(2)、若∠BAC=∠DAC,求证:四边形 EBFD 是菱形.17. 如图,AE∥BF,BD平分∠ABC 交AE 于点D,点 C 在 BF 上,且BC=AB,连结 CD.求证:四边形 ABCD 是菱形.
(1)、求证:四边形 EBFD是平行四边形.(2)、若∠BAC=∠DAC,求证:四边形 EBFD 是菱形.17. 如图,AE∥BF,BD平分∠ABC 交AE 于点D,点 C 在 BF 上,且BC=AB,连结 CD.求证:四边形 ABCD 是菱形. 18. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD相交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
18. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD相交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD,
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框“”内打“√" ;若赞成小洁的说法,请你补充一个条件,并证明.

