华师大版数学八年级下册19.1 矩形 同步测试
试卷更新日期:2024-02-22 类型:同步测试
一、选择题
-
1. 如图,EF过矩形ABCD对角线的交点O,且分别交AB,CD 于点E,F,则阴影部分的面积是矩形ABCD 面积的 ( )
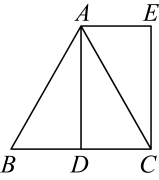
 A、 B、 C、 D、2. 已知矩形的一边长为6cm,一条对角线的长为10 cm,则矩形的面积为( )A、12 cm2 B、24 cm2 C、48 cm2 D、60 cm23. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,若∠ADB=40°,则∠E的度数是( )
A、 B、 C、 D、2. 已知矩形的一边长为6cm,一条对角线的长为10 cm,则矩形的面积为( )A、12 cm2 B、24 cm2 C、48 cm2 D、60 cm23. 如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,若∠ADB=40°,则∠E的度数是( ) A、20° B、25° C、30° D、35°4. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A、20° B、25° C、30° D、35°4. 如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )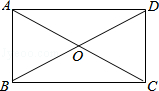 A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB5. 如图,在矩形ABCD中,O是BC的中点,∠AOD = 90°,若矩形ABCD的周长为30 cm,则AB的长为( )
A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OB5. 如图,在矩形ABCD中,O是BC的中点,∠AOD = 90°,若矩形ABCD的周长为30 cm,则AB的长为( ) A、5 cm B、10 cm C、15 cm D、7.5 cm6. 如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是( )
A、5 cm B、10 cm C、15 cm D、7.5 cm6. 如图,平行四边形ABCD的对角线AC与BD相交于点O,添加一个条件使平行四边形ABCD为矩形的是( )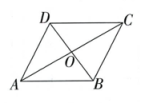 A、AD=AB B、AB⊥AD C、AB=AC D、CA⊥BD7. 如图,在中, , , , P为边上一动点,于点E , 于点F , 则的最小值为( )
A、AD=AB B、AB⊥AD C、AB=AC D、CA⊥BD7. 如图,在中, , , , P为边上一动点,于点E , 于点F , 则的最小值为( ) A、 B、 C、 D、68. 如图,用一根绳子检测一个平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量两条对角线就可以判断了.在如下定理中:
A、 B、 C、 D、68. 如图,用一根绳子检测一个平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量两条对角线就可以判断了.在如下定理中:①两组对边分别相等的四边形是平行四边形,②对角线相等的平行四边形是矩形,③矩形的四个角都是直角,④三个角都是直角的四边形是矩形,这种检测方法用到的数学根据是( )
 A、① B、② C、③ D、④9. 如图,某超市在门口离地高米的墙上,装有一个由传感器控制的门铃 , 如图 , 人只要移至距该门铃米及米以内时,门铃会自动发出语音“欢迎光临”.如图②,一个身高米的顾客走到处,门铃恰好自动响起,则的长为( )
A、① B、② C、③ D、④9. 如图,某超市在门口离地高米的墙上,装有一个由传感器控制的门铃 , 如图 , 人只要移至距该门铃米及米以内时,门铃会自动发出语音“欢迎光临”.如图②,一个身高米的顾客走到处,门铃恰好自动响起,则的长为( )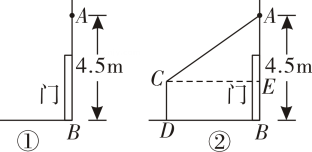 A、6米 B、5米 C、4米 D、3米10. 如图,在平面直角坐标系中,的顶点、的坐标分别为、 , , , 过作轴垂线交轴于点 , 作轴垂线交轴于点 , 则矩形的面积为( )
A、6米 B、5米 C、4米 D、3米10. 如图,在平面直角坐标系中,的顶点、的坐标分别为、 , , , 过作轴垂线交轴于点 , 作轴垂线交轴于点 , 则矩形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
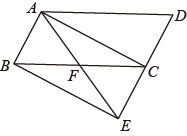
11. 如图,四边形ABDE是矩形,AC⊥DC于点C,交BD于点F,AE=AC,∠ADE=62° ,则∠BAF的度数为°
 12. 如图,在矩形中,对角线与相交于点 , 垂直且平分线段 , 垂足为点 , , 则的长为 .
12. 如图,在矩形中,对角线与相交于点 , 垂直且平分线段 , 垂足为点 , , 则的长为 . 13. 如图,在矩形中,对角线和交于点O , 若 , 则 .
13. 如图,在矩形中,对角线和交于点O , 若 , 则 .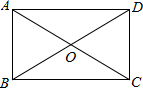 14. 如图,在Rt△ABC中,∠ABC=90°,过点B作BE⊥AC,延长BE到点D,使得 BD=AC,连接AD,CD,若AB=4,AD=5,则CD的长为 .
14. 如图,在Rt△ABC中,∠ABC=90°,过点B作BE⊥AC,延长BE到点D,使得 BD=AC,连接AD,CD,若AB=4,AD=5,则CD的长为 . 15. 已知,矩形 , 为的中点,为上一点,连接 , 若 , , , 则的长为 .
15. 已知,矩形 , 为的中点,为上一点,连接 , 若 , , , 则的长为 .三、解答题
-
16. 如图,在矩形ABCD 中,E,F分别是边 BC,AD 上的点,且AE=CF.
 (1)、求证:△ABE≌△CDF.(2)、当AC⊥EF时,四边形 AECF 是菱形吗? 请说明理由.17. 如图,在平面直角坐标系中,矩形 OABC 的顶点 B 的坐标为(12,5).若直线恰好将矩形OABC 分成面积相等的两部分,求 b的值.
(1)、求证:△ABE≌△CDF.(2)、当AC⊥EF时,四边形 AECF 是菱形吗? 请说明理由.17. 如图,在平面直角坐标系中,矩形 OABC 的顶点 B 的坐标为(12,5).若直线恰好将矩形OABC 分成面积相等的两部分,求 b的值.