备考2024年高考数学提升专题特训:平面解析几何
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
1. 如图,平面 , 四边形是正方形,且 , 试求:
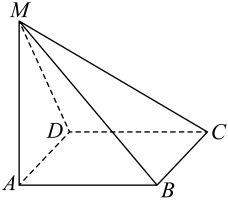 (1)、点到的距离;(2)、求异面直线与所成的角.2. 已知椭圆的上、下顶点分别为 , 短轴长为在上(不与重合),且.(1)、求的标准方程;(2)、直线分别交直线于两点,连接交于另一点 , 证明:直线过定点.3. 在平面直角坐标系中,直线的参数方程为(为参数),以左边原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为 .(1)、求直线的直角坐标方程以及曲线的普通方程;(2)、过直线上一点作曲线的切线,切点为 , 求的最小值.4. 已知点和直线 , 动点到点的距离与到直线的距离之比为.(1)、求动点的轨迹的方程;(2)、过点的直线交于两点,若点的坐标为 , 直线与轴的交点分别是 , 证明:线段的中点为定点.5. 已知双曲线的实轴长为4,且与双曲线有公共的焦点.(1)、求双曲线的方程;(2)、已知 , 是双曲线上的任意一点,求的最小值.6. 已知的顶点.(1)、求边上的中线所在直线的方程;(2)、求经过点 , 且在轴上的截距和轴上的截距相等的直线的方程.7. 在平面直角坐标系中,已知 , 点M满足 , 记的轨迹为曲线.(1)、求曲线的方程;(2)、设圆 , 若直线l过圆的圆心且与曲线交于两点,且 , 求直线l的方程.8. 某圆拱桥的水面跨度16m,拱高4m,现有一船,宽10m,水面以上高3m,问这条船能否通过?9. 已知圆C: .(1)、设点 , 过点M作直线l与圆C交于A , B两点,若 , 求直线l的方程;(2)、设P是直线上的点,过P点作圆C的切线PA , PB , 切点为A , B , 求证:经过A , P , C三点的圆必过定点,并求出所有定点的坐标.10. 已知圆经过点和 , 且圆心在直线上.(1)、求圆的方程;(2)、设直线经过点 , 且与圆相切,求直线的方程.(3)、为圆上任意一点,在(1)的条件下,求的最小值.11. 已知抛物线:()经过点.(1)、求抛物线的方程及其焦点坐标、准线方程;(2)、过抛物线上一动点作圆:的一条切线,切点为 , 求切线长的最小值.12. 已知椭圆左焦点
(1)、点到的距离;(2)、求异面直线与所成的角.2. 已知椭圆的上、下顶点分别为 , 短轴长为在上(不与重合),且.(1)、求的标准方程;(2)、直线分别交直线于两点,连接交于另一点 , 证明:直线过定点.3. 在平面直角坐标系中,直线的参数方程为(为参数),以左边原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为 .(1)、求直线的直角坐标方程以及曲线的普通方程;(2)、过直线上一点作曲线的切线,切点为 , 求的最小值.4. 已知点和直线 , 动点到点的距离与到直线的距离之比为.(1)、求动点的轨迹的方程;(2)、过点的直线交于两点,若点的坐标为 , 直线与轴的交点分别是 , 证明:线段的中点为定点.5. 已知双曲线的实轴长为4,且与双曲线有公共的焦点.(1)、求双曲线的方程;(2)、已知 , 是双曲线上的任意一点,求的最小值.6. 已知的顶点.(1)、求边上的中线所在直线的方程;(2)、求经过点 , 且在轴上的截距和轴上的截距相等的直线的方程.7. 在平面直角坐标系中,已知 , 点M满足 , 记的轨迹为曲线.(1)、求曲线的方程;(2)、设圆 , 若直线l过圆的圆心且与曲线交于两点,且 , 求直线l的方程.8. 某圆拱桥的水面跨度16m,拱高4m,现有一船,宽10m,水面以上高3m,问这条船能否通过?9. 已知圆C: .(1)、设点 , 过点M作直线l与圆C交于A , B两点,若 , 求直线l的方程;(2)、设P是直线上的点,过P点作圆C的切线PA , PB , 切点为A , B , 求证:经过A , P , C三点的圆必过定点,并求出所有定点的坐标.10. 已知圆经过点和 , 且圆心在直线上.(1)、求圆的方程;(2)、设直线经过点 , 且与圆相切,求直线的方程.(3)、为圆上任意一点,在(1)的条件下,求的最小值.11. 已知抛物线:()经过点.(1)、求抛物线的方程及其焦点坐标、准线方程;(2)、过抛物线上一动点作圆:的一条切线,切点为 , 求切线长的最小值.12. 已知椭圆左焦点 、右顶点 , 过且斜率为的直线l与椭圆交于两点,求的面积. 13. 设双曲线的离心率为 , 且顶点到渐近线的距离为.已知直线过点 , 直线与双曲线的左,右两支的交点分别为 , 直线与双曲线的渐近线的交点为 , 其中点在轴的右侧.设的面积分别是.(1)、求双曲线的方程;(2)、求的取值范围.14. 设椭圆的上顶点为 , 左焦点为 . 且在直线上.(1)、求的标准方程;(2)、若直线与交于两点,且点为中点,求直线的方程.15. 已知抛物线
、右顶点 , 过且斜率为的直线l与椭圆交于两点,求的面积. 13. 设双曲线的离心率为 , 且顶点到渐近线的距离为.已知直线过点 , 直线与双曲线的左,右两支的交点分别为 , 直线与双曲线的渐近线的交点为 , 其中点在轴的右侧.设的面积分别是.(1)、求双曲线的方程;(2)、求的取值范围.14. 设椭圆的上顶点为 , 左焦点为 . 且在直线上.(1)、求的标准方程;(2)、若直线与交于两点,且点为中点,求直线的方程.15. 已知抛物线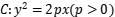 上的点
上的点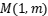 到焦点F的距离为4. (1)、求C的方程;(2)、若过点F的直线与C交于不同的两点A , B , 且 , 求直线AB的方程.16. 已知椭圆的左,右焦点分别为 , , 离心率为 , M为椭圆C上的一个动点,且点M到右焦点距离的最大值为 .(1)、求椭圆C的方程;(2)、已知过点的直线l交椭圆C于A , B两点,当的面积最大时,求此时直线l的方程.17. “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图)
到焦点F的距离为4. (1)、求C的方程;(2)、若过点F的直线与C交于不同的两点A , B , 且 , 求直线AB的方程.16. 已知椭圆的左,右焦点分别为 , , 离心率为 , M为椭圆C上的一个动点,且点M到右焦点距离的最大值为 .(1)、求椭圆C的方程;(2)、已知过点的直线l交椭圆C于A , B两点,当的面积最大时,求此时直线l的方程.17. “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动,在我国源远流长.某些折纸活动蕴含丰富的数学内容,例如:用一张圆形纸片,按如下步骤折纸(如图)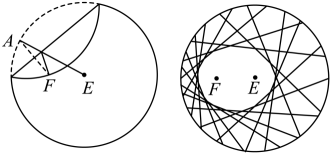
步骤1:设圆心是 , 在圆内异于圆心处取一点,标记为;
步骤2:把纸片折叠,使圆周正好通过点;
步骤3:把纸片展开,并留下一道折痕;
步骤4:不停重复步骤2和3,就能得到越来越多的折痕.
现对这些折痕所围成的图形进行建模研究.若取半径为6的圆形纸片,如图,设定点到圆心的距离为4,按上述方法折纸.以点所在的直线为轴,线段中点为原点建立平面直角坐标系.
(1)、若已研究出折痕所围成的图形即是折痕与线段交点的轨迹,求折痕围成的椭圆的标准方程;(2)、记(1)问所得图形为曲线 , 若过点且不与轴垂直的直线与椭圆交于两点,在轴的正半轴上是否存在定点 , 使得直线斜率之积为定值?若存在,求出该定点和定值;若不存在,请说明理由.18. 已知椭圆:的长轴长是短轴长的倍.(1)、求的方程;(2)、若倾斜角为的直线与交于 , 两点,线段的中点坐标为 , 求.