备考2024年高考数学提升专题特训:空间向量与立体几何
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
1. 已知PA垂直于正方形ABCD所在的平面,M,N分别在AB,PC上,且PN=2NC,AM=2MB,PA=AD=1,如图建立空间直角坐际系,求的坐标.
 2. 如图,在平行六面体中,以顶点A为端点的三条棱长度都为2,且两两夹角为 .
2. 如图,在平行六面体中,以顶点A为端点的三条棱长度都为2,且两两夹角为 . (1)、求的长;(2)、求与所成角的余弦值.3. 如图,三棱柱中,M , N分别是上
(1)、求的长;(2)、求与所成角的余弦值.3. 如图,三棱柱中,M , N分别是上 点,且 . 设 , , .
点,且 . 设 , , .  (1)、试用 , , 表示向量;(2)、若 , 求MN的长.4. 如图在四面体中, , , , 为线段中点,
(1)、试用 , , 表示向量;(2)、若 , 求MN的长.4. 如图在四面体中, , , , 为线段中点, (1)、用基底表示向量 , 并求线段的长度;(2)、求异面直线与所成角的余弦值.5. 如图,已知平行六面体中,底面是边长为的正方形,(1)、求;(2)、求 .6. 如图,在直四棱柱中, , , , E , F , G分别为棱 , , 的中点.
(1)、用基底表示向量 , 并求线段的长度;(2)、求异面直线与所成角的余弦值.5. 如图,已知平行六面体中,底面是边长为的正方形,(1)、求;(2)、求 .6. 如图,在直四棱柱中, , , , E , F , G分别为棱 , , 的中点. (1)、求的值;(2)、证明:C , E , F , G四点共面.7. 《九章算术》中将四个面都为直角三角形的四面体称为鳖臑.如图,在鳖臑中,平面 , 平面 , 为的中点, .
(1)、求的值;(2)、证明:C , E , F , G四点共面.7. 《九章算术》中将四个面都为直角三角形的四面体称为鳖臑.如图,在鳖臑中,平面 , 平面 , 为的中点, . (1)、设 , , , 用 , , 表示;(2)、若求 .8. 如图,在三棱锥中,平面 , , , , , 分别是 , , , 的中点, , 与交于点 , 与交于点 , 连接.
(1)、设 , , , 用 , , 表示;(2)、若求 .8. 如图,在三棱锥中,平面 , , , , , 分别是 , , , 的中点, , 与交于点 , 与交于点 , 连接. (1)、求证:;(2)、求平面与平面夹角的余弦值;(3)、求点到平面的距离.9. 在长方体中, , 点是棱上一点,且.
(1)、求证:;(2)、求平面与平面夹角的余弦值;(3)、求点到平面的距离.9. 在长方体中, , 点是棱上一点,且. (1)、证明:;(2)、若二面角的的大小为 , 求的值.10. 如图,在直三棱柱中, , .
(1)、证明:;(2)、若二面角的的大小为 , 求的值.10. 如图,在直三棱柱中, , . (1)、求证:;(2)、求点到平面的距离.11. 已知空间三点 , , , 设 , .(1)、求;(2)、与互相垂直,求实数的值.12. 如图,三棱柱的体积为 , 侧面是矩形, , , 且已知二面角是钝角.
(1)、求证:;(2)、求点到平面的距离.11. 已知空间三点 , , , 设 , .(1)、求;(2)、与互相垂直,求实数的值.12. 如图,三棱柱的体积为 , 侧面是矩形, , , 且已知二面角是钝角. (1)、求的长度;(2)、求二面角的大小.13. 已知平面向量 , , , 且 .(1)、求的坐标;(2)、求向量在向量上的投影向量的模.14. 已知椭圆过两点,O为坐标原点.(1)、求椭圆的标准方程;(2)、若直线与圆相切,且与椭圆交于A,B两点,证明: .15. 如图所示的多面体中,底面ABCD为矩形,平面ABCD , 平面ABCD , 平面ABCD , , 且AB=4,BC=2, , BE=1.
(1)、求的长度;(2)、求二面角的大小.13. 已知平面向量 , , , 且 .(1)、求的坐标;(2)、求向量在向量上的投影向量的模.14. 已知椭圆过两点,O为坐标原点.(1)、求椭圆的标准方程;(2)、若直线与圆相切,且与椭圆交于A,B两点,证明: .15. 如图所示的多面体中,底面ABCD为矩形,平面ABCD , 平面ABCD , 平面ABCD , , 且AB=4,BC=2, , BE=1. (1)、求BF的长;(2)、求直线与平面成的角的正弦值.16. 已知点.(1)、若 , 且 , 求的坐标;(2)、求以为邻边的平行四边形的面积.17. 如图,在四棱锥中,底面为直角梯形, , , , , E为的中点,且 .
(1)、求BF的长;(2)、求直线与平面成的角的正弦值.16. 已知点.(1)、若 , 且 , 求的坐标;(2)、求以为邻边的平行四边形的面积.17. 如图,在四棱锥中,底面为直角梯形, , , , , E为的中点,且 . (1)、求证:平面;(2)、记的中点为N,若M在线段上,且直线与平面所成角的正弦值为 , 求线段的长.18. 如图,在四棱台中,已知 , .
(1)、求证:平面;(2)、记的中点为N,若M在线段上,且直线与平面所成角的正弦值为 , 求线段的长.18. 如图,在四棱台中,已知 , .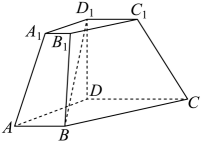 (1)、证明:平面;(2)、若四棱台的体积为 , 求二面角的余弦值.19. 如图,在四棱锥中,平面平面 , , , , , , 为中点,点在上,且 .
(1)、证明:平面;(2)、若四棱台的体积为 , 求二面角的余弦值.19. 如图,在四棱锥中,平面平面 , , , , , , 为中点,点在上,且 . (1)、求证:平面;(2)、求平面与平面夹角的余弦值;(3)、线段上是否存在点 , 使得平面 , 说明理由?20. 如图,四棱锥的底面是正方形,平面 .
(1)、求证:平面;(2)、求平面与平面夹角的余弦值;(3)、线段上是否存在点 , 使得平面 , 说明理由?20. 如图,四棱锥的底面是正方形,平面 .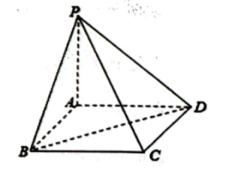 (1)、求证:平面平面;(2)、求平面与平面夹角的正弦值.21. 在四棱锥中,底面ABCD为直角梯形,BCAD , ∠ADC=90°, , E为线段AD的中点.底面ABCD , 点F是棱长PC的中点,平面BEF与棱PD相交于点G.
(1)、求证:平面平面;(2)、求平面与平面夹角的正弦值.21. 在四棱锥中,底面ABCD为直角梯形,BCAD , ∠ADC=90°, , E为线段AD的中点.底面ABCD , 点F是棱长PC的中点,平面BEF与棱PD相交于点G.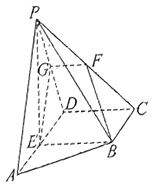 (1)、求证:BEFG;(2)、若PC与AB所成的角为 , 求直线PB与平面BEF所成角的正弦值.22. 如图,在四棱锥中,则面底面 , 侧棱 , 底面为直角梯形,其中 , , , 为中点.
(1)、求证:BEFG;(2)、若PC与AB所成的角为 , 求直线PB与平面BEF所成角的正弦值.22. 如图,在四棱锥中,则面底面 , 侧棱 , 底面为直角梯形,其中 , , , 为中点.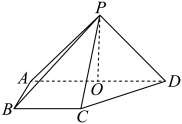 (1)、求证:平面;(2)、求异面直线与所成角的大小.23. 如图,四棱锥的底面是等腰梯形, , 底面为棱上的一点.
(1)、求证:平面;(2)、求异面直线与所成角的大小.23. 如图,四棱锥的底面是等腰梯形, , 底面为棱上的一点. (1)、证明:;(2)、若二面角的余弦值为 , 求的值.
(1)、证明:;(2)、若二面角的余弦值为 , 求的值.