备考2024年高考数学优生冲刺专题特训:空间向量与立体几何
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
1. 如图所示,已知P是平行四边形ABCD所在平面外一点,连接PA , PB , PC , PD , 点E , F , G , H分别为 , , , 的重心.求证:E , F , G , H四点共面.
 2. 如图,在四棱锥中, , , , 点M为棱PA的中点.
2. 如图,在四棱锥中, , , , 点M为棱PA的中点. (1)、设 , , , 用 , , 表示 , ;(2)、若底面ABCD,且 , 求平面BCM与平面ABCD所成角的余弦值.3. 如图,在三棱柱中,所有棱长都为2,且 , 平面平面 , 点为的中点,点为的中点.
(1)、设 , , , 用 , , 表示 , ;(2)、若底面ABCD,且 , 求平面BCM与平面ABCD所成角的余弦值.3. 如图,在三棱柱中,所有棱长都为2,且 , 平面平面 , 点为的中点,点为的中点.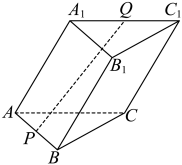 (1)、点到直线的距离;(2)、求点到平面的距离.4. 如图,在四棱锥P-ABCD中,CD∥AB,∠ABC=90°,AB=2BC=2CD=4,三棱锥B-PAD的体积为.
(1)、点到直线的距离;(2)、求点到平面的距离.4. 如图,在四棱锥P-ABCD中,CD∥AB,∠ABC=90°,AB=2BC=2CD=4,三棱锥B-PAD的体积为.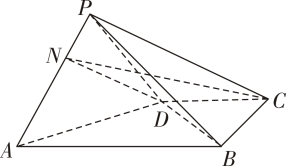 (1)、求点P到平面ABCD的距离;(2)、若PA=PD,平面PAD⊥平面ABCD,点N在线段AP上,AN=2NP,求平面NCD与平面ABCD夹角的余弦值.5. 如图,在直三棱柱中,D , E分别是棱AB , 的中点, , .
(1)、求点P到平面ABCD的距离;(2)、若PA=PD,平面PAD⊥平面ABCD,点N在线段AP上,AN=2NP,求平面NCD与平面ABCD夹角的余弦值.5. 如图,在直三棱柱中,D , E分别是棱AB , 的中点, , . (1)、求证:平面;(2)、再从条件①、条件②、条件③这三个条件中选择一个作为已知,使得各条件相融.并求直线与平面所成的角的正弦值.
(1)、求证:平面;(2)、再从条件①、条件②、条件③这三个条件中选择一个作为已知,使得各条件相融.并求直线与平面所成的角的正弦值.条件①:;条件②:;条件③:到平面的距离为1.
6. 如图,在三棱锥 P-ABC中,平面 PAB⊥平面ABC,AB=4,BC=2,AC=PA=PB=2 , D,E分别为PC,PA的中点.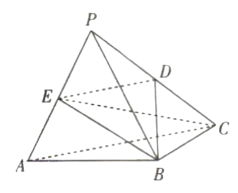 (1)、证明:平面 BCE⊥平面 PAB.(2)、求平面 PBC与平面BDE 的夹角的余弦值.7. 如图,在平行六面体中, , , , , 点为中点.
(1)、证明:平面 BCE⊥平面 PAB.(2)、求平面 PBC与平面BDE 的夹角的余弦值.7. 如图,在平行六面体中, , , , , 点为中点.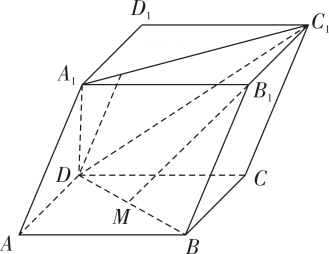 (1)、证明:平面;(2)、求二面角的正弦值.8. 如图,在多面体中,底面为菱形,平面 , , 且为棱的中点,为棱上的动点.
(1)、证明:平面;(2)、求二面角的正弦值.8. 如图,在多面体中,底面为菱形,平面 , , 且为棱的中点,为棱上的动点.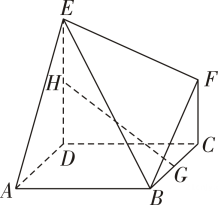 (1)、求二面角的正弦值;(2)、是否存在点使得平面?若存在,求的值;否则,请说明理由.9. 如图,矩形中为边的中点,将沿直线翻折成 , 使 , 若为线段的中点,
(1)、求二面角的正弦值;(2)、是否存在点使得平面?若存在,求的值;否则,请说明理由.9. 如图,矩形中为边的中点,将沿直线翻折成 , 使 , 若为线段的中点,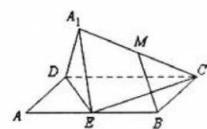 (1)、求证:平面(2)、求证:平面平面(3)、求二面角夹角的正弦值10. 如图,在四棱锥中,底面是菱形,与交于点 , , 平面 , 为线段上的一点.
(1)、求证:平面(2)、求证:平面平面(3)、求二面角夹角的正弦值10. 如图,在四棱锥中,底面是菱形,与交于点 , , 平面 , 为线段上的一点.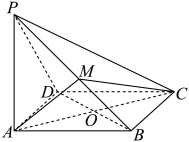 (1)、证明:平面平面 ;(2)、当与平面所成的角的正弦值最大时,求平面与平面夹角的余弦值.11. 在正六棱柱中,底面棱长为 , 高为 , 分别为 , 的中点,连接.
(1)、证明:平面平面 ;(2)、当与平面所成的角的正弦值最大时,求平面与平面夹角的余弦值.11. 在正六棱柱中,底面棱长为 , 高为 , 分别为 , 的中点,连接.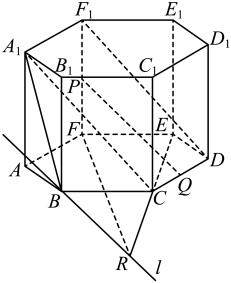 (1)、求所成角的余弦值;(2)、过点作直线 , 设点是直线上一点,记平面与平面所成角为 , 求的取值范围.12. 底面ABCD和侧面均为矩形, , , , .
(1)、求所成角的余弦值;(2)、过点作直线 , 设点是直线上一点,记平面与平面所成角为 , 求的取值范围.12. 底面ABCD和侧面均为矩形, , , , . (1)、求证:;(2)、求与平面所成角的正弦值.13. 如图,在正三棱台中, , .
(1)、求证:;(2)、求与平面所成角的正弦值.13. 如图,在正三棱台中, , . (1)、证明:.(2)、过的平面α交分别于 , 若平面 , 求直线与平面所成角的正弦值.14. 如图,在正三棱台中, , D,E分别为 , 的中点.
(1)、证明:.(2)、过的平面α交分别于 , 若平面 , 求直线与平面所成角的正弦值.14. 如图,在正三棱台中, , D,E分别为 , 的中点. (1)、证明:平面;(2)、设P,Q分别为棱AB,BC上的点,且 , D,P,Q均在平面上,若与的面积比为3:8,
(1)、证明:平面;(2)、设P,Q分别为棱AB,BC上的点,且 , D,P,Q均在平面上,若与的面积比为3:8,(i)证明:
(ii)求与平面所成角的正弦值.
15. 如图,在四棱锥中, , 四边形是菱形,是棱上的动点,且 . (1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由.16. 如图,在矩形ABCD中, , , M是线段AD上的一动点,将沿着BM折起,使点A到达点A'的位置,满足点平面BCDM且点A'在平面BCDM内的射影E落在线段BC上.
(1)、证明:平面 .(2)、是否存在实数 , 使得平面与平面所成锐二面角的余弦值是?若存在,求出的值;若不存在,请说明理由.16. 如图,在矩形ABCD中, , , M是线段AD上的一动点,将沿着BM折起,使点A到达点A'的位置,满足点平面BCDM且点A'在平面BCDM内的射影E落在线段BC上. (1)、当点M与端点D重合时,证明:平面ACD';(2)、求三棱锥E-A'BM的体积的最大值;(3)、设直线CD与平面A'BM所成的角为 , 二面角A'-BM-C的平面角为 , 求的最大值.17. 已知在四棱锥中, , , , , E为CD的中点.
(1)、当点M与端点D重合时,证明:平面ACD';(2)、求三棱锥E-A'BM的体积的最大值;(3)、设直线CD与平面A'BM所成的角为 , 二面角A'-BM-C的平面角为 , 求的最大值.17. 已知在四棱锥中, , , , , E为CD的中点. (1)、证明:平面平面PAE;(2)、若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求二面角的正弦值.18. 如图,四棱柱的底面ABCD为直角梯形, , , , 直线与直线CD所成的角取得最大值.点M为的中点,且 .
(1)、证明:平面平面PAE;(2)、若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求二面角的正弦值.18. 如图,四棱柱的底面ABCD为直角梯形, , , , 直线与直线CD所成的角取得最大值.点M为的中点,且 . (1)、证明:平面平面;(2)、若钝二面角的余弦值为 , 当时,求三棱锥的体积.
(1)、证明:平面平面;(2)、若钝二面角的余弦值为 , 当时,求三棱锥的体积.

