备考2024年高考数学提升专题特训:立体几何初步
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
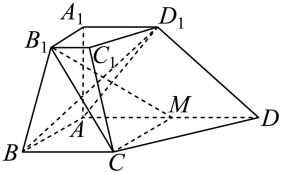
1. 如图,在正方体ABCD﹣A1B1C1D1中,E,F,G,M,N分别是B1C1 , A1D1 , A1B1 , BD,B1C的中点,求证:
 (1)、MN∥平面CDD1C1 .(2)、平面EBD∥平面FGA.2. 如图,长方体的体积是24,E为的中点,平面将长方体分成三棱锥和多面体两部分.
(1)、MN∥平面CDD1C1 .(2)、平面EBD∥平面FGA.2. 如图,长方体的体积是24,E为的中点,平面将长方体分成三棱锥和多面体两部分. (1)、若 , 求多面体的表面积;(2)、求三棱锥的体积.3. 如图,在四棱锥P-ABCD中,底面ABCD是菱形,AB=2, , △PAB是正三角形,平面PAB⊥平面ABCD,点Q是线段PC的中点.
(1)、若 , 求多面体的表面积;(2)、求三棱锥的体积.3. 如图,在四棱锥P-ABCD中,底面ABCD是菱形,AB=2, , △PAB是正三角形,平面PAB⊥平面ABCD,点Q是线段PC的中点.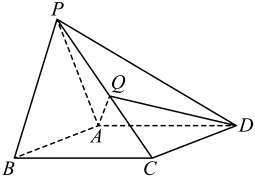 (1)、求三棱锥Q-PAD的体积;(2)、求平面PBC与平面BCD夹角的余弦值.4. 在正三棱台中, , , 为中点,在上,.
(1)、求三棱锥Q-PAD的体积;(2)、求平面PBC与平面BCD夹角的余弦值.4. 在正三棱台中, , , 为中点,在上,. (1)、请作出与平面的交点 , 并写出与的比值(在图中保留作图痕迹,不必写出画法和理由);(2)、求直线与平面所成角的正弦值.5. 圆柱的轴截面ABCD是正方形,是底面圆周上一点,DC与AE成角, .
(1)、请作出与平面的交点 , 并写出与的比值(在图中保留作图痕迹,不必写出画法和理由);(2)、求直线与平面所成角的正弦值.5. 圆柱的轴截面ABCD是正方形,是底面圆周上一点,DC与AE成角, . (1)、求直线AC与平面BCE所成角的正弦值;(2)、求点B到平面AEC的距离.6.
(1)、求直线AC与平面BCE所成角的正弦值;(2)、求点B到平面AEC的距离.6.如图,长方体ABCD﹣A1B1C1D1中被截去一部分,
(1)其中EF∥A1D1 . 剩下的几何体是什么?截取的几何体是什么?
(2)若FH∥EG,但FH<EG,截取的几何体是什么?
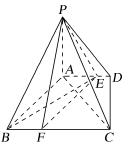
 7. 已知四棱锥 (图1)的三视图如图2所示, 为正三角形, 垂直底面 ,俯视图是直角梯形.
7. 已知四棱锥 (图1)的三视图如图2所示, 为正三角形, 垂直底面 ,俯视图是直角梯形. 图1
图1  图2(1)、求正视图的面积;(2)、求四棱锥 的体积;(3)、求证: 平面 .8. 如图,在三棱柱中, , , , 分别是 , , , 的中点.求证:
图2(1)、求正视图的面积;(2)、求四棱锥 的体积;(3)、求证: 平面 .8. 如图,在三棱柱中, , , , 分别是 , , , 的中点.求证: (1)、 , , , 四点共面;(2)、 .9. 如图,是一个几何体的三视图,若它的体积是 , 求a的值,并求此几何体的表面积.
(1)、 , , , 四点共面;(2)、 .9. 如图,是一个几何体的三视图,若它的体积是 , 求a的值,并求此几何体的表面积. 10. 如图,在正六棱锥中,为底面中心, , .
10. 如图,在正六棱锥中,为底面中心, , . (1)、若 , 分别是棱 , 的中点,证明:平面;(2)、若该正六棱锥的顶点都在球的表面上,求球的表面积和体积.11. 台州黄岩被誉为“模具之乡”,为市场对球形冰淇淋的需求,特地制作了一款中空的正三棱柱模具,其内壁恰好是球体的表面,且内壁与棱柱的每一个面都相切内壁厚度忽略不计 , 店家可以将不同口味的冰淇淋放入该模具中,再通过按压的方式得到球形冰淇淋已知该模具底部边长为 .
(1)、若 , 分别是棱 , 的中点,证明:平面;(2)、若该正六棱锥的顶点都在球的表面上,求球的表面积和体积.11. 台州黄岩被誉为“模具之乡”,为市场对球形冰淇淋的需求,特地制作了一款中空的正三棱柱模具,其内壁恰好是球体的表面,且内壁与棱柱的每一个面都相切内壁厚度忽略不计 , 店家可以将不同口味的冰淇淋放入该模具中,再通过按压的方式得到球形冰淇淋已知该模具底部边长为 .
⑴求内壁的面积;
⑵求制作该模具所需材料的体积;
⑶求模具顶点到内壁的最短距离.
12. 如图,已知平面四边形存在外接圆,且 , , . (1)、求的面积;(2)、求的周长的最大值.13. 如图,在多面体中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E , F两点,上、下底面矩形的长、宽分别为c , d与a , b , 且a>c , b>d , 两底面间的距离为h .
(1)、求的面积;(2)、求的周长的最大值.13. 如图,在多面体中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E , F两点,上、下底面矩形的长、宽分别为c , d与a , b , 且a>c , b>d , 两底面间的距离为h .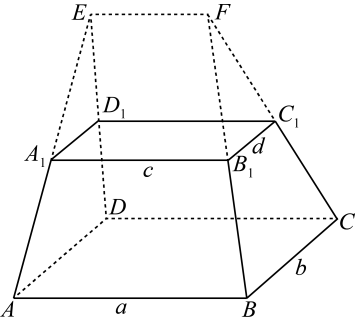 (1)、求侧面与底面所成二面角的大小;(2)、证明:;(3)、在估测该多面体的体积时,经常运用近似公式来计算,已知它的体积公式是 , 试判断与V的大小关系,并加以证明.
(1)、求侧面与底面所成二面角的大小;(2)、证明:;(3)、在估测该多面体的体积时,经常运用近似公式来计算,已知它的体积公式是 , 试判断与V的大小关系,并加以证明.注:与两个底面平行,且到两个底面距离相等的截面称为该多面体的中截面.
14. 如图,圆柱内接于球O,已知球O的半径R=2,设圆柱的底面半径为r. (1)、以r为变量,表示圆柱的表面积和体积;(2)、当r为何值时,该球内接圆柱的侧面积最大,最大值是多少?15. 如图,在长方体中,E , F分别是和的中点.
(1)、以r为变量,表示圆柱的表面积和体积;(2)、当r为何值时,该球内接圆柱的侧面积最大,最大值是多少?15. 如图,在长方体中,E , F分别是和的中点. (1)、证明:E , F , D , B四点共面.(2)、证明:BE , DF , 三线共点.16. 如图,平行六面体的底面是菱形,且
(1)、证明:E , F , D , B四点共面.(2)、证明:BE , DF , 三线共点.16. 如图,平行六面体的底面是菱形,且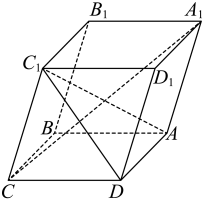 (1)、用空间的一个基底表示 , 并求的长;(2)、求异面直线与所成角的余弦值.17. 在四棱锥中,平面平面 , 侧面是等边三角形, , , 在棱上,且满足.
(1)、用空间的一个基底表示 , 并求的长;(2)、求异面直线与所成角的余弦值.17. 在四棱锥中,平面平面 , 侧面是等边三角形, , , 在棱上,且满足.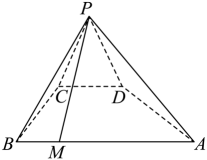 (1)、求证:;(2)、求二面角的余弦值.18. 如图,正四棱柱中,M为的中点, , .
(1)、求证:;(2)、求二面角的余弦值.18. 如图,正四棱柱中,M为的中点, , . (1)、求证:平面;(2)、求二面角的余弦值.19. 如图, 已知正方体 的棱长为为的中点.
(1)、求证:平面;(2)、求二面角的余弦值.19. 如图, 已知正方体 的棱长为为的中点. (1)、求证: 平面;(2)、求平面 与平面夹角的余弦值。20. 如图,在棱长为2的正方体中,为棱的中点,为棱的中点.
(1)、求证: 平面;(2)、求平面 与平面夹角的余弦值。20. 如图,在棱长为2的正方体中,为棱的中点,为棱的中点. (1)、求证:平面;(2)、求直线与平面所成角的正弦值.21. 如图所示,在四棱锥中,底面为矩形,侧面为正三角形,且分别为的中点,在线段上,且 .
(1)、求证:平面;(2)、求直线与平面所成角的正弦值.21. 如图所示,在四棱锥中,底面为矩形,侧面为正三角形,且分别为的中点,在线段上,且 .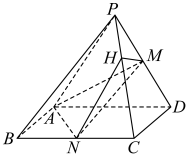 (1)、求证:平面;(2)、当时,求平面与平面的夹角的余弦值.
(1)、求证:平面;(2)、当时,求平面与平面的夹角的余弦值.