备考2024年高考数学优生冲刺专题特训:立体几何初步
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
1. 如图,在四面体P-ABC中,△ABC是等腰三角形AB⊥BC , .
 (1)、证明:PB⊥AC;(2)、若AB=2, , PA⊥AB.
(1)、证明:PB⊥AC;(2)、若AB=2, , PA⊥AB.(ⅰ)求点A到平面PBC的距离;
(ⅱ)求二面角的正弦值.
2. 如图,在直三棱柱 中,底面是等腰直角三角形,且 , . (1)、求该直三棱柱的表面积;(2)、若把两个这样的直三棱柱拼成一个大棱柱,求大棱柱表面积的最小值,并求出此时大棱柱的外接球的直径3. 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形ABCD并求出其面积.
(1)、求该直三棱柱的表面积;(2)、若把两个这样的直三棱柱拼成一个大棱柱,求大棱柱表面积的最小值,并求出此时大棱柱的外接球的直径3. 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′,如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形ABCD并求出其面积. 4. 如图,正方体 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知 为柱 上一点(不在点 、 处), ( ),菜农需要在地面正方形 内画出一条曲线 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点 为地面正方形 内的曲线 上任意一点,设 、 分别为在P点处观测E和 的仰角.
4. 如图,正方体 是一个棱长为2的空心蔬菜大棚,由8个钢结构(地面没有)组合搭建而成的,四个侧面及顶上均被可采光的薄膜覆盖,已知 为柱 上一点(不在点 、 处), ( ),菜农需要在地面正方形 内画出一条曲线 将菜地分隔为两个不同的区域来种植不同品种的蔬菜以加强管理,现已知点 为地面正方形 内的曲线 上任意一点,设 、 分别为在P点处观测E和 的仰角. (1)、若 ,请说明曲线 是何种曲线,为什么?(2)、若E为柱 的中点,且 时,请求出点P所在区域的面积.5. 如图,在正三棱柱中,分别为的中点.
(1)、若 ,请说明曲线 是何种曲线,为什么?(2)、若E为柱 的中点,且 时,请求出点P所在区域的面积.5. 如图,在正三棱柱中,分别为的中点. (1)、证明:平面平面.(2)、若侧面的中心为为侧面内的一个动点,平面 , 且的轨迹长度为 , 求三棱柱的表面积.6. 如图,四棱锥中,平面 , 四边形是矩形,、分别是、的中点.若 , .(1)、求证:平面;
(1)、证明:平面平面.(2)、若侧面的中心为为侧面内的一个动点,平面 , 且的轨迹长度为 , 求三棱柱的表面积.6. 如图,四棱锥中,平面 , 四边形是矩形,、分别是、的中点.若 , .(1)、求证:平面; (2)、求点到平面的距离;(3)、求直线与平面所成角的正弦值.7. 如图,在直三棱柱ABC—中,底面△ABC是以角B为直角的等腰直角三角形,且腰长为2,D为BC的中点,三棱柱体积
(2)、求点到平面的距离;(3)、求直线与平面所成角的正弦值.7. 如图,在直三棱柱ABC—中,底面△ABC是以角B为直角的等腰直角三角形,且腰长为2,D为BC的中点,三棱柱体积 (1)、求三棱柱的外接球的表面积和体积;(2)、求三棱锥的体积.8. 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
(1)、求三棱柱的外接球的表面积和体积;(2)、求三棱锥的体积.8. 如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1. (1)、若D为线段AC的中点,求证:AC⊥平面PDO;(2)、求三棱锥P-ABC体积的最大值;(3)、若 ,点E在线段PB上,求CE+OE的最小值.9. 在中,内角 , , 的对边分别为 , , , 且 .(1)、求角的大小(2)、若 , 点是的重心,且 , 求内切圆的半径.10. 如图,在多面体ABCDE中,面BCDE为平行四边形, , , , , F为AC中点.
(1)、若D为线段AC的中点,求证:AC⊥平面PDO;(2)、求三棱锥P-ABC体积的最大值;(3)、若 ,点E在线段PB上,求CE+OE的最小值.9. 在中,内角 , , 的对边分别为 , , , 且 .(1)、求角的大小(2)、若 , 点是的重心,且 , 求内切圆的半径.10. 如图,在多面体ABCDE中,面BCDE为平行四边形, , , , , F为AC中点.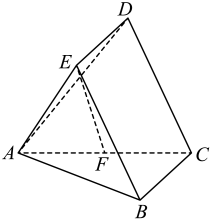 (1)、求证:;(2)、二面角的正切值为4,求多面体ABCDE的体积.11. 如图,在正方体中,为的中点,为的中点,求证:
(1)、求证:;(2)、二面角的正切值为4,求多面体ABCDE的体积.11. 如图,在正方体中,为的中点,为的中点,求证: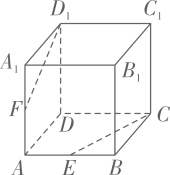 (1)、 , , , 四点共面;(2)、 , , 三线共点.12. 在长方体中, , M为中点, .
(1)、 , , , 四点共面;(2)、 , , 三线共点.12. 在长方体中, , M为中点, .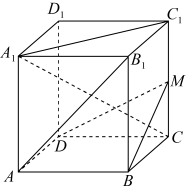 (1)、求异面直线与所成角的余弦值;(2)、 分别为直线上的点,求的最小值.13. 如图,已知正方体的棱长为2,点M为正方形的内切圆上的动点.
(1)、求异面直线与所成角的余弦值;(2)、 分别为直线上的点,求的最小值.13. 如图,已知正方体的棱长为2,点M为正方形的内切圆上的动点.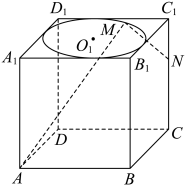 (1)、在线段上是否存在点N , 使得恒成立,若存在,求出点N的位置,若不存在,说明理由;(2)、当点M落在线段靠近点上时,求二面角的余弦值.14. 如图,在四棱锥中,底面
(1)、在线段上是否存在点N , 使得恒成立,若存在,求出点N的位置,若不存在,说明理由;(2)、当点M落在线段靠近点上时,求二面角的余弦值.14. 如图,在四棱锥中,底面 正方形,平面平面 , 点在线段上,平面 , , .
正方形,平面平面 , 点在线段上,平面 , , .  (1)、求证:为的中点;(2)、求二面角的大小;(3)、求直线与平面所成角的正弦值.15. 两个边长为2的正方形和各与对方所在平面垂直,、分别是对角线、上的点,且.
(1)、求证:为的中点;(2)、求二面角的大小;(3)、求直线与平面所成角的正弦值.15. 两个边长为2的正方形和各与对方所在平面垂直,、分别是对角线、上的点,且.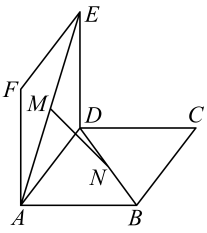 (1)、求证:平面;(2)、设 , , 求与的函数关系式;(3)、求、两点间的最短距离.16. 如图,直线平面 , 直线平行四边形
(1)、求证:平面;(2)、设 , , 求与的函数关系式;(3)、求、两点间的最短距离.16. 如图,直线平面 , 直线平行四边形 , 四棱锥
, 四棱锥 的顶点在平面上, , , , , 分别是与的中点.
的顶点在平面上, , , , , 分别是与的中点.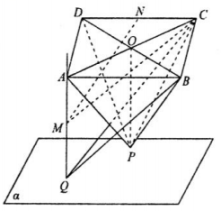 (1)、求证:平面;(2)、求二面角的余弦值.
(1)、求证:平面;(2)、求二面角的余弦值.