备考2024年高考数学优生冲刺专题特训：微积分与极限

试卷更新日期：2024-02-22 类型：三轮冲刺

进入出卷网下载

一、解答题

1. 设f(a)＝ $\int_{0}^{1}$ |x²－a²|dx

(1)、当0≤a≤1与a＞1时，分别求f(a)；

(2)、当a≥0时，求f(a)的最小值．

查看试题解析
2. 请先阅读：
在等式 $cos 2 x = 2 {cos}^{2} x - 1$ （ $x \in R$ ）的两边求导，得： ${(cos 2 x)}^{'} = {(2 {cos}^{2} x - 1)}^{'}$ ，

由求导法则，得 $(- sin 2 x) \cdot 2 = 4 cos x \cdot (- sin x)$ ，化简得等式： $sin 2 x = 2 cos x \cdot sin x$ 。

(1)、利用上题的想法（或其他方法），结合等式 ${(1+x)}^{n} {=C}_{n}^{0} + C_{n}^{1} x + C_{n}^{2} x^{2} + \dots + C_{n}^{n} x^{n}$ （ $x \in R$ ，正整数 $n \geq 2$ ），证明： $n [{(1 + x)}^{n - 1} - 1] = \sum_{k = 2}^{n} k C_{n}^{k} x^{k - 1}$ 。

(2)、对于正整数 $n \geq 3$ ，求证：
（i） $\sum_{k = 1}^{n} {(- 1)}^{k} k C_{n}^{k} = 0$ ；（ii） $\sum_{k = 1}^{n} {(- 1)}^{k} k^{2} C_{n}^{k} = 0$ ；（iii） $\sum_{k = 1}^{n} \frac{1}{k + 1} C_{n}^{k} = \frac{2^{n + 1} - 1}{n + 1}$ 。

查看试题解析
3. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $a_{1} = 2, a_{2} = 4$ 且满足: $a_{n} + a_{n + 1} = 3 S_{n - 1} + 6 (n \geq 2)$

(1)、证明： ${a_{n}}$ 是等比数列，并求数列 ${a_{n}}$ 的通项公式.

(2)、设 $b_{n} = t^{n} (2 n - 1) a_{n}, (t \neq 0)$ ，若数列 ${b_{n}}$ 是等差数列，求实数 $t$ 的值；

(3)、在(2)的条件下，设 $c_{n} = \frac{2^{n + 1}}{2^{2 n + 1} - 3 \cdot 2^{n} + 1} (n \in N^{*}),$ 记数列 ${c_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，若对任意的 $n, k \in N^{*},$ 存在实数 $λ$ ,使得 $λ \cdot T_{n} < b_{k + 1}$ ,求实数 $λ$ 的最大值.

查看试题解析
4. 设数列 ${a_{n}} (n = 1, 2, \dots)$ 是等差数列，且公差为d ，若数列 ${a_{n}}$ 中任意（不同）两项之和仍是该数列中的一项，则称该数列是“封闭数列”.

(1)、若 $a_{1} = 4, d = 2$ ，求证：该数列是“封闭数列”；

(2)、试判断数列 $a_{n} = 2 n - 7 (n \in N^{*})$ 是否是“封闭数列”，为什么?

(3)、设 $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，若公差 $d = 1, a_{1} > 0$ ，试问：是否存在这样的“封闭数列”，使 $\lim_{n \to \infty} (\frac{1}{S_{1}} + \frac{1}{S_{2}} + \dots + \frac{1}{S_{n}}) = \frac{11}{9}$ ；若存在，求 ${a_{n}}$ 的通项公式，若不存在，说明理由.

查看试题解析
5. 已知函数 $f (x) = e^{x} - a x^{2}$ ， $f^{'} (x)$ 是 $f (x)$ 的导函数．

(1)、若关于 $x$ 的方程 $f^{'} (x) = 0$ 有两个不同的正实根，求 $a$ 的取值范围；

(2)、当 $x \geq 0$ 时， $f (x) \geq (e - 2) x + a$ 恒成立，求 $a$ 的取值范围．（参考数据： $l n 2 \approx 0.69$ ）

查看试题解析
6. 已知函数 $f (x) = e^{x} - \frac{a}{x + 1} (a \in R)$ .

(1)、若函数 $f (x)$ 的图象在点 $P (0 ， f (0))$ 处的切线 $l$ 与直线 $3 x - y - 6 = 0$ 平行，求切线 $l$ 的方程；

(2)、若函数 $f (x)$ 有两个零点，求实数 $a$ 的取值范围.

查看试题解析
7. 已知 $a ， k \in R$ ，设函数 $f (x) = l n (x + a) - k a x$ ．

(1)、当 $k = 1$ 时，若函数 $f (x)$ 在 $(- a ， + \infty)$ 上单调递增，求实数 $a$ 的取值范围；

(2)、若对任意实数 $a$ ，函数 $f (x)$ 均有零点，求实数 $k$ 的最大值；

(3)、若函数 $f (x)$ 有两个零点 $x_{1} ， x_{2}$ ，证明： $x_{1} x_{2} + a (x_{1} + x_{2}) < \frac{1}{k^{2} a^{2}}$ ．

查看试题解析
8. 已知函数 $f (x) = e^{x} \cdot | x - 1 | - a (a \in R)$ .

(1)、判断 $f (x) = 0$ 的根的个数；

(2)、若函数 $t (x) = f (x - \frac{1}{2}) (x \in [0 ， 1.7])$ 有两个零点 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，证明： $x_{2} - x_{1} < \frac{(e + 1) a}{e}$ .

查看试题解析
9. 已知函数 $f (x) = l n x - a x + a (a \in R)$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 在 $(1 ， + \infty)$ 上有零点 $x_{0}$ ，
①求a的取值范围；

②求证： $\frac{2 - a}{a} < x_{0} < e^{\frac{1}{a}}$ ．

查看试题解析
10. 如图：已知 $y = a x^{2} + b x$ 通过点（1，2），与 $y = - x^{2} + 2 x$ 有一个交点横坐标为 $x_{1}$ ，且 $a < 0 ， a \neq - 1$ .

(1)、求 $y = a x^{2} + b x$ 与 $y = - x^{2} + 2 x$ 所围的面积 $S$ 与 $a$ 的函数关系；

(2)、当 $a ， b$ 为何值时， $S$ 取得最小值.

查看试题解析
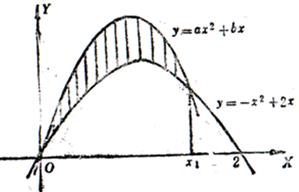11. 某工厂共有10台机器，生产一种仪器元件，由于受生产能力和技术水平等因素限制，会产生一定数量的次品．根据经验知道，若每台机器产生的次品数P（万件）与每台机器的日产量x（万件）（4≤x≤12）之间满足关系：P=0.1x²﹣3.2lnx+3，已知每生产1万件合格的元件可以盈利2万元，但每产生1万件装次品将亏损1万元．（利润=盈利﹣亏损）
（I）试将该工厂每天生产这种元件所获得的利润y（万元）表示为x的函数；
（II）当每台机器的日产量x（万件）写为多少时所获得的利润最大，最大利润为多少？

查看试题解析
12. 已知函数f(x)=f'(1)e^x-1-f(0)x+ $\frac{1}{2}$ x³

(1)、求f(x)的解析式及单调区间；

(2)、若f(x)≥ $\frac{1}{2}$ x²+ax+b，求(a＋1)b的最大值.

查看试题解析
13. 已知函数 $f (x) = \frac{\ln x}{e^{t x}}$ ， $t \in R$ ，其中 $e = 2.71828 \cdot \cdot \cdot$ 是自然对数的底数．

(1)、若 $f (x)$ 有两个极值点，求实数 $t$ 的取值范围；

(2)、若存在正数 $x_{0}$ ，使得对任意 $x > 0$ 均有 $f (x) \leq f (x_{0})$ 成立．
证明：（ⅰ） $e^{t x_{0}} > 1 + \log_{x_{0}} 2$ ；

（ⅱ） $f (x_{0}) < \frac{e^{t x_{0}}}{t x_{0}} - \frac{1}{3} t^{2} x_{0}^{2} - 2$ ．

查看试题解析
14. 已知 $f (x) = \frac{ln x}{x}$ ，直线 $l$ 为曲线 $y = f (x)$ 在 $(t ， f (t))$ 处的切线，直线 $l$ 与曲线 $y = f (x)$ 相交于点 $(s ， f (s))$ 且 $s < t$ .

(1)、求 $t$ 的取值范围；

(2)、（i）证明： $ln x \leq 1 + \frac{1}{e} \cdot (x - e) - \frac{1}{2 e^{2}} \cdot {(x - e)}^{2} + \frac{1}{3 e^{3}} \cdot {(x - e)}^{3}$ ；
（ii）证明： $s > \frac{11}{2} t - 3 t ln t$ .

查看试题解析
15. 已知函数 $f (x) = a x^{2} + x - e^{x}$ .

(1)、若 $a = \frac{1}{2}$ ，讨论 $f (x)$ 的单调性；

(2)、若 $f (x) \leq 1$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
16. 已知函数 $f (x) = \frac{2}{3} x^{3} - (2 a + 1) x^{2} + 4 a x + \frac{16}{3} a^{2}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 只有1个零点 $x_{0}$ ，且 $x_{0} < 0$ ，求 $a$ 的取值范围；

(3)、当 $a = - \frac{1}{4}$ 时，是否存在正整数k，使得关于x的方程 $| f (\sin x) + f (\cos x) | = k$ 有解？如果存在，求出k的值；如果不存在，说明理由．

查看试题解析
17. 已知函数 $f (x) = a e^{x} - x - 1 (a \in R) ， g (x) = x^{2}$ .

(1)、讨论函数 $f (x)$ 的单调性；

(2)、当 $a > 0$ 时，若曲线 $C_{1} ： y = f (x) + x + 1$ 与曲线 $C_{2} ： y = g (x)$ 存在唯一的公切线，求实数 $a$ 的值；

(3)、当 $a = 1 ， x \geq 0$ 时，不等式 $f (x) \geq k x l n (x + 1)$ 恒成立，求实数 $k$ 的取值范围.

查看试题解析
18. 已知函数 $f (x) = \frac{x}{e^{x} - 1}$ ．

(1)、判断并证明 $f (x)$ 在 $(1 ， + \infty)$ 的单调性；

(2)、已知a为正实数，且对于任意 $x \in (0 ， + \infty)$ ，都有 $(e^{x} + a) f (x) \geq 2 a$ 恒成立，求正实数a的取值范围．

查看试题解析
19. 已知函数 $f (x) = a \ln (a x) + \frac{1}{x^{2}} (a > 0)$ .

(1)、当 $a = 1$ 时，求 $f (x)$ 的单调区间；

(2)、若关于 $x$ 的不等式 $e^{x} + \frac{1}{x^{2}} \geq f (x)$ 恒成立，求a的取值范围.

查看试题解析
20. 已知函数 $f (x) = \frac{1}{3} x^{3} - a x + 2 a$ ．

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 只有一个零点，求 $a$ 的取值范围．

查看试题解析