备考2024年高考数学提升专题特训:一元函数导数及其应用
试卷更新日期:2024-02-22 类型:三轮冲刺
一、解答题
-
1. 求函数 在 附近的平均变化率,并求出在该点处的导数.
2. 在 赛车中,赛车位移与比赛时间 存在函数关系 ( 的单位为 , 的单位为 ).求:
(1)、 , 时的 与 ;(2)、 时的瞬时速度.3. 已知曲线 .求:(1)、曲线C上横坐标为1的点处的切线方程;(2)、(1)中的切线与曲线C是否还有其他的公共点?4. 已知曲线 经过点 ,求:(1)、曲线在点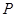 处的切线的方程; (2)、过点 的曲线C的切线方程.5. 已知函数在点处的切线与直线垂直.(1)、求;(2)、求的单调区间和极值.6. 已知函数 .(1)、求曲线在处的切线方程;(2)、若对 , 恒成立.求实数的取值范围.7. 已知函数的部分图象如图所示, ω>0, , 且.
处的切线的方程; (2)、过点 的曲线C的切线方程.5. 已知函数在点处的切线与直线垂直.(1)、求;(2)、求的单调区间和极值.6. 已知函数 .(1)、求曲线在处的切线方程;(2)、若对 , 恒成立.求实数的取值范围.7. 已知函数的部分图象如图所示, ω>0, , 且. (1)、求与的值;(2)、若斜率为的直线与曲线相切,求切点坐标.8. 设函数f(x)=x3+ax2+bx+1的导数 满足 , ,其中常数a , b∈R.(1)、求曲线y=f(x)在点(1,f(1))处的切线方程;(2)、设 ,求函数g(x)的极值.9. 已知函数 .(1)、如果a>0,函数在区间 上存在极值,求实数a的取值范围;(2)、当x≥1时,不等式 恒成立,求实数k的取值范围.10. 已知函数(1)、当时, 求的极值;(2)、若曲线与曲线存在2 条公切线, 求a的取值范围.11. 求下列函数的导数:(1)、;(2)、 ;(3)、 .12. 记 , 分别为函数 , 的导函数.若存在 , 满足且 , 则称为函数与的一个“点”.(1)、证明:函数与不存在“点”;(2)、若函数与存在“点”,求实数的值;(3)、已知 , . 若存在实数 , 使函数与在区间内存在“点”,求实数的取值范围.13. 已知函数 .(1)、讨论函数 的单调性;(2)、若不等式对恒成立, 求的取值范围.14. 已知函数.(1)、求的单调区间;(2)、若在上恒成立,求证:.15. 已知函数(是自然对数的底数).(1)、讨论函数的单调性;(2)、若有两个零点,求实数的取值范围.16. 已知函数.(1)、讨论的单调性;(2)、若 , 求的取值范围.17. 已知函数.(1)、若 , 求实数的取值范围;(2)、若有两个极值点分别为 , , 求的最小值.18. 从今年起,我国将于每年5月第四周开展“全国城市生活垃圾分类宣传周”活动,首全国城市生活垃圾分类宣传周时间为2023年5月22日至28日,宣传主题为“让垃圾分类成为新时尚”,在此宣传周期间,某社区举行了一次生活垃圾分类知识比赛.要求每个家庭派出一名代表参赛,每位参赛者需测试A , B , C三个项目,三个测试项目相互不受影响.(1)、若某居民甲在测试过程中,第一项测试是等可能的从三个项目中选一项测试,且他测试三个项目“通过”的概率分别为.求他第一项测试“通过”的概率;(2)、现规定:三个项目全部通过获得一等奖,只通过两项获得二等奖,只通过一项获得三等奖,三项都没有通过不获奖.已知居民乙选择的顺序参加测试,且他前两项通过的概率均为 , 第三项通过的概率为.若他获得一等奖的概率为 , 求他获得二等奖的概率的最小值.19. 已知函数 , .(1)、若 , 求函数的图象在点处的切线方程;(2)、若在上恒成立,求实数的最大值.
(1)、求与的值;(2)、若斜率为的直线与曲线相切,求切点坐标.8. 设函数f(x)=x3+ax2+bx+1的导数 满足 , ,其中常数a , b∈R.(1)、求曲线y=f(x)在点(1,f(1))处的切线方程;(2)、设 ,求函数g(x)的极值.9. 已知函数 .(1)、如果a>0,函数在区间 上存在极值,求实数a的取值范围;(2)、当x≥1时,不等式 恒成立,求实数k的取值范围.10. 已知函数(1)、当时, 求的极值;(2)、若曲线与曲线存在2 条公切线, 求a的取值范围.11. 求下列函数的导数:(1)、;(2)、 ;(3)、 .12. 记 , 分别为函数 , 的导函数.若存在 , 满足且 , 则称为函数与的一个“点”.(1)、证明:函数与不存在“点”;(2)、若函数与存在“点”,求实数的值;(3)、已知 , . 若存在实数 , 使函数与在区间内存在“点”,求实数的取值范围.13. 已知函数 .(1)、讨论函数 的单调性;(2)、若不等式对恒成立, 求的取值范围.14. 已知函数.(1)、求的单调区间;(2)、若在上恒成立,求证:.15. 已知函数(是自然对数的底数).(1)、讨论函数的单调性;(2)、若有两个零点,求实数的取值范围.16. 已知函数.(1)、讨论的单调性;(2)、若 , 求的取值范围.17. 已知函数.(1)、若 , 求实数的取值范围;(2)、若有两个极值点分别为 , , 求的最小值.18. 从今年起,我国将于每年5月第四周开展“全国城市生活垃圾分类宣传周”活动,首全国城市生活垃圾分类宣传周时间为2023年5月22日至28日,宣传主题为“让垃圾分类成为新时尚”,在此宣传周期间,某社区举行了一次生活垃圾分类知识比赛.要求每个家庭派出一名代表参赛,每位参赛者需测试A , B , C三个项目,三个测试项目相互不受影响.(1)、若某居民甲在测试过程中,第一项测试是等可能的从三个项目中选一项测试,且他测试三个项目“通过”的概率分别为.求他第一项测试“通过”的概率;(2)、现规定:三个项目全部通过获得一等奖,只通过两项获得二等奖,只通过一项获得三等奖,三项都没有通过不获奖.已知居民乙选择的顺序参加测试,且他前两项通过的概率均为 , 第三项通过的概率为.若他获得一等奖的概率为 , 求他获得二等奖的概率的最小值.19. 已知函数 , .(1)、若 , 求函数的图象在点处的切线方程;(2)、若在上恒成立,求实数的最大值.