备考2024年高考数学优生冲刺专题特训：三角函数

试卷更新日期：2024-02-22 类型：三轮冲刺

进入出卷网下载

一、解答题

1. 如图所示为圆柱形大型储油罐固定在 $U$ 型槽上的横截面图，已知图中 $A B C D$ 为等腰梯形（ $A B$ ∥ $D C$ ），支点 $A$ 与 $B$ 相距8 $m$ ，罐底最低点到地面 $C D$ 距离为1 $m$ ，设油罐横截面圆心为 $O$ ，半径为5 $m$ ， $∠ D = 56 °$ ，求： $U$ 型槽的横截面（阴影部分）的面积.（参考数据： $\sin 53 ° \approx 0.8$ ， $\tan 56 ° \approx 1.5$ ， $π \approx 3$ ，结果保留整数）

查看试题解析
2. 如图，公园里有一湖泊，其边界由两条线段 $A B ， A C$ 和以 $B C$ 为直径的半圆弧 $\overset{⌢}{B C}$ 组成，其中 $A C$ 为2百米， $A C ⊥ B C ， ∠ A$ 为 $\frac{π}{3}$ ．若在半圆弧 $\overset{⌢}{B C}$ ，线段 $A C$ ，线段 $A B$ 上各建一个观赏亭 $D ， E ， F$ ，再修两条栈道 $D E ， D F$ ，使 $D E / / A B ， D F / / A C$ . 记 $∠ C B D = θ (\frac{π}{3} \leq θ < \frac{π}{2})$ ．

(1)、试用 $θ$ 表示 $B D$ 的长；

(2)、试确定点 $E$ 的位置，使两条栈道长度之和最大.

查看试题解析
3. 已知函数 $g (x) = s i n^{2} x - c o s x + a ， x \in (\frac{π}{2} ， π)$ 有两个零点.

(1)、求实数a的取值范围.

(2)、设 $x_{1} ， x_{2}$ 是 $g (x)$ 的两个零点，证明： $x_{1} + x_{2} < \frac{3 π}{2}$

查看试题解析
4. 在锐角 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c ， S$ 为 $△ A B C$ 的面积，且 $a^{2} = 2 S + (b - c)^{2}$ ．

(1)、求 $t a n A$ 的值；

(2)、若 $a = 8$ ，证明： $16 < b + c \leq 8 \sqrt{5}$ ．

查看试题解析
5. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别是 $a ， b ， c$ ，且 $\sqrt{3} s i n C + c o s C = \frac{a + c}{b} ， c = 2$ ．

(1)、求角 $B$ 的大小；

(2)、若 $△ A B C$ 是锐角三角形，求 $△ A B C$ 的面积的取值范围．

查看试题解析
6. 某校兴趣小组在如图所示的矩形区域ABCD内举行机器人拦截挑战赛，在E处按 $\vec{E P}$ 方向释放机器人甲，同时在A处按 $\vec{A Q}$ 方向释放机器人乙，设机器人乙在M处成功拦截机器人甲，两机器人停止运动.若点M在矩形区域ABCD内（包含边界），则挑战成功，否则挑战失败.已知 $A B = 6$ 米，E为AB中点，比赛中两机器人均匀速直线运动方式行进，记 $\vec{E P}$ 与 $\vec{E B}$ 的夹角为 $θ (0 < θ < π)$ ， $\vec{A Q}$ 与 $\vec{A B}$ 的夹角为 $α (0 < α < \frac{π}{2})$ .

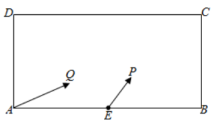(1)、若两机器人运动方向的夹角为 $\frac{π}{3}$ ， AD足够长，机器人乙挑战成功，求两机器人运动路程和的最大值；

(2)、已知机器人乙的速度是机器人甲的速度的2倍.
①若 $θ = \frac{π}{3}$ ， AD足够长，机器人乙挑战成功，求 $s i n α$ .
②如何设计矩形区域ABCD的宽AD的长度，才能确保无论 $θ$ 的值为多少，总可以通过设置机器人乙的释放角度 $α$ 使机器人乙挑战成功？

查看试题解析
7. 已知函数 $f (x) = A c o s (ω x + φ) (A > 0 ， ω > 0 ， 0 < φ < π)$ 的部分图象如图所示.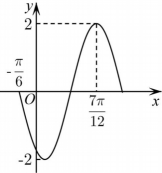

(1)、求 $f (x)$ 的解析式；

(2)、设 $0 < θ < π$ ，记 $f (x)$ 在区间 $[0 ， θ]$ 上的最大值为 $g (θ)$ ，求 $g (θ)$ 的解析式.

查看试题解析
8. 若 $f (x) = c o s 2 x - 2 a c o s x - 2 a$ 的最小值为 $g (a)$ .

(1)、求 $g (a)$ 的表达式；

(2)、求能使 $g (a) = \frac{1}{2}$ 的 $a$ 的值，并求当 $a$ 取此值时， $f (x)$ 的最大值.

查看试题解析
9. 网络购物行业日益发达，各销售平台通常会配备送货上门服务．小金正在配送客户购买的电冰箱，并获得了客户所在小区门户以及建筑转角处的平面设计示意图．

(1)、为避免冰箱内部制冷液逆流，要求运送过程中发生倾斜时，外包装的底面与地面的倾斜角 $α$ 不能超过 $\frac{π}{4}$ ，且底面至少有两个顶点与地面接触．外包装看作长方体，如图1所示，记长方体的纵截面为矩形 $A B C D$ ， $A D = 0.8 m$ ， $A B = 2.4 m$ ，而客户家门高度为 $2.3$ 米，其他过道高度足够．若以倾斜角 $α = \frac{π}{4}$ 的方式进客户家门，小金能否将冰箱运送入客户家中？计算并说明理由．

(2)、由于客户选择以旧换新服务，小金需要将客户长方体形状的旧冰箱进行回收．为了省力，小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上，平板车长宽均小于冰箱背面）．推运过程中遇到一处直角过道，如图2所示，过道宽为 $1.8$ 米．记此冰箱水平截面为矩形 $E F G H$ ， $E H = 1.2 m$ ．设 $∠ P H G = β$ ，当冰箱被卡住时(即点 $H$ 、 $G$ 分别在射线 $P R$ 、 $P Q$ 上，点 $O$ 在线段 $E F$ 上），尝试用 $β$ 表示冰箱高度 $E F$ 的长，并求出 $E F$ 的最小值，最后请帮助小金得出结论：按此种方式推运的旧冰箱，其高度的最大值是多少？（结果精确到 $0.1 m$ ）

查看试题解析
10. 在 $Δ A B C$ 中角A ， B ， C所对的边分别为a，b ， c ，满足 $2 a s i n A c o s B + b s i n 2 A = 2 \sqrt{3} a c o s C ，$

(1)、求角C的大小；

(2)、若 $c = 2 \sqrt{3}$ ， $∠ A B C$ 的平分线与 $∠ B A C$ 的平分线交于点I ，求 $Δ A B I$ 周长的最大值．

查看试题解析
11. 设函数 $f (x) = c o s x c o s (x - \frac{π}{6}) + \sqrt{3} s i n^{2} x - \frac{3 \sqrt{3}}{4}$ ．

(1)、求 $f (x)$ 的最小正周期和单调递增区间；

(2)、当 $x \in [\frac{π}{12} ， \frac{π}{2}]$ 时，求函数 $f (x)$ 的最大值及此时的 $x$ 值．

查看试题解析
12. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ，且 $2 c s i n^{2} (\frac{π}{4} - \frac{B}{2}) + b c o s \frac{C}{2} = c$ ．

(1)、求角 $C$ 的大小；

(2)、 $B = \frac{π}{2}$ ， $B C = 2$ ，点 $O$ 为线段 $B C$ 的中点，点 $M$ 、 $N$ 分别在线段 $A B$ 和 $A C$ 上，满足 $O M ⊥ O N$ ，求 $△ O M N$ 面积的最小值．

查看试题解析
13. 蜂房是自然界最神奇的“建筑”之一，如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥 $H - A B C$ ， $J - C D E$ ， $K - E F A$ ，再分别以 $A C$ ， $C E$ ， $E A$ 为轴将 $△ A C H$ ， $△ C E J$ ， $△ E A K$ 分别向上翻转 $180 °$ ，使 $H$ ， $J$ ， $K$ 三点重合为点 $S$ 所围成的曲顶多面体（下底面开口），如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画，定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和，而每一顶点的曲率规定等于 $2 π$ 减去蜂房多面体在该点的各个面角之和（多面体的面角是多面体的面的内角，用弧度制表示）.例如：正四面体在每个顶点有3个面角，每个面角是 $\frac{π}{3}$ ，所以正四面体在各顶点的曲率为 $2 π - 3 \times \frac{π}{3} = π$ .

(1)、求蜂房曲顶空间的弯曲度；

(2)、若正六棱柱底面边长为1，侧棱长为2，设 $B H = x$
①用 $x$ 表示蜂房（图2右侧多面体）的表面积 $S (x)$ ；
②当蜂房表面积最小时，求其顶点 $S$ 的曲率的余弦值.

查看试题解析
14. 定义： $μ = \frac{1}{n} [s i n^{2} (θ_{1} - θ_{0}) + s i n^{2} (θ_{2} - θ_{0}) + ⋯ + s i n^{2} (θ_{n} - θ_{0})]$ 为实数 $θ_{1}$ ， $θ_{2}$ ， …， $θ_{n}$ 对 $θ_{0}$ 的“正弦方差”.

(1)、若 $θ_{1} = \frac{π}{3}$ ， $θ_{2} = \frac{2 π}{3}$ ， $θ_{3} = π$ ，证明：实数 $θ_{1}$ ， $θ_{2}$ ， $θ_{3}$ 对 $θ_{0}$ 的“正弦方差” $μ$ 的值是与 $θ_{0}$ 无关的定值；

(2)、若 $θ_{1} = \frac{π}{4}$ ， $θ_{2} = α$ ， $θ_{3} = β$ ， $α \in (\frac{π}{2} ， π)$ ， $β \in (π ， 2 π)$ ，若实数 $θ_{1}$ ， $θ_{2}$ ， $θ_{3}$ 对 $θ_{0}$ 的“正弦方差” $μ$ 的值是与 $θ_{0}$ 无关的定值，求 $α$ ， $β$ 值.

查看试题解析
15. 如图所示，某小区中心有一块圆心角为 $60 °$ ，半径为 $8 \sqrt{3} m$ 的扇形空地，现计划将该区域设计成亲子室外游乐区域，根据设计要求，需要铺设一块平行四边形的塑胶地面EFPQ（其中点E ， F在边OA上，点 $Q$ 在边OB上，点 $P$ 在AB上），其他区域地面铺设绿地，设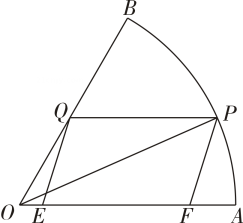 $∠ P O A = θ$ .

(1)、 $θ$ 表示绿地的面积 $S$ ；

(2)、若铺设绿地每平分米100元，要使得铺设绿地的出用 $W$ 最低， $θ$ 应取何值，并求出此时 $W$ 的值．

查看试题解析
16. 如图，摄影爱好者在某公园A处，发现正前方B处有一立柱，测得立柱顶端O的仰角和立柱底部B的俯角均为 $30 °$ ，已知摄影爱好者的身高约为 $\sqrt{3}$ 米（将眼睛S距地面的距离SA按 $\sqrt{3}$ 米处理）．

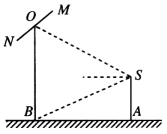(1)、求摄影爱好者到立柱的水平距离AB和立柱的高度OB；

(2)、立柱的顶端有一长为2米的彩杆MN，且MN绕其中点O在摄影爱好者与立柱所在的平面内旋转．在彩杆转动的任意时刻，摄影爱好者观察彩杆MN的视角 $∠ M S N$ （设为 $θ$ ）是否存在最大值？若存在，请求出 $∠ M S N$ 取最大值时 $c o s θ$ 的值；若不存在，请说明理由．

查看试题解析
17. 整治人居环境，打造美丽乡村，某村准备将一块由一个半圆和长方形组成的空地进行美化，如图，长方形的边 $A B$ 为半圆的直径，O为半圆的圆心， $A B = 2 A D = 200 m$ ，现要将此空地规划出一个等腰三角形区域 $P M N$ （底边 $M N ⊥ C D$ ）种植观赏树木，其余的区域种植花卉.设 $∠ M O B = θ ， θ \in (0 ， \frac{π}{2}]$ .

(1)、当 $θ = \frac{π}{3}$ 时，求 $M N$ 的长；

(2)、求三角形区域 $P M N$ 面积的最大值.

查看试题解析
18. 某城市公园有一如图所示的绿化带，其形状由一个直径为 $2 km$ 的半圆 $O$ 和矩形 $A B C D$ 组成，其中 $A B = 1 km$ .管理部门规划在圆心 $O$ 处建造一个亭子，为了方便游客到亭子游玩，决定从A地出发修建一条经过亭子 $O$ 处到达 $B C$ 的公路，具体路线是：在半圆 $O$ 上选点 $E$ (异于 $A$ ， $D$ 点)，从点 $A$ 沿圆弧到点 $E$ ，再从点 $E$ 经过亭子 $O$ 的直线到达 $B C$ 边上的点 $F$ 处.已知从点 $A$ 到点 $E$ 的修路费用每千米需要 $\frac{1}{5} a$ 元，从点 $E$ 到点 $F$ 的修路费用每千米需要 $\frac{1}{6} a$ 元，设 $∠ A O E = θ$ 弧度，从 $A$ 地经点 $E$ ， $O$ 到 $F$ 地修路所需费用为 $y$ 元.

(1)、试将 $y$ 表示为 $θ$ 的函数 $y = f (θ)$ ，并写出定义域；

(2)、当 $\cos θ$ 取何值时，修路所需费用最少?

查看试题解析
19. 已知函数 $f (x) = A \sin (ω x + \frac{π}{6}) (A > 0, ω > 0)$ 只能同时满足下列三个条件中的两个：①图象上一个最低点为 $M (\frac{2 π}{3}, - 2)$ ；②函数 $f (x)$ 的图象可由 $y = \sqrt{2} \sin (x - \frac{π}{4})$ 的图象平移得到；③若对任意 $x \in R$ ， $f (x_{1}) \leq f (x) \leq f (x_{2})$ 恒成立，且 $| x_{1} - x_{2} |$ 的最小值为 $\frac{π}{2}$ .

(1)、请写出这两个条件序号，并求出 $f (x)$ 的解析式；

(2)、求方程 $f (x) - 1 = 0$ 在区间 $[- π, π]$ 上所有解的和.

查看试题解析