吉林省四平市铁西区2023-2024学年七年级上学期期中考试数学试题

试卷更新日期：2024-02-22 类型：期中考试

进入出卷网下载

一、单项选择题（每题2分，共12分）

1. 3的绝对值是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、-3

查看试题解析
2. 现有4种说法：① $- a$ 表示负数；②绝对值最小的有理数是0；③ $3 \times 1 0^{2} x^{2} y$ 是5次单项式；④ $\frac{x - y}{5}$ 是多项式.其中正确的是（）

A、①3 B、②④ C、②③ D、①④

查看试题解析
3. 如果 $a + b > 0 ， a b < 0$ 那么（）

A、a，b异号，且 $| a | > | b |$ B、a，b异号，且 $a > b$ C、a，b异号，其中正数的绝对值大 D、 $a > 0 > b$ 或 $a < 0 < b$

查看试题解析
4. 下列式子中去括号正确的是（）

A、 $- (x - 2 y) = - x - 2 y$ B、 $+ (- 3 a + b) = 3 a + b$ C、 $x + 2 (x^{2} - y^{2}) = x + 2 x^{2} + y^{2}$ D、 $3 x^{2} - 3 (x + 6) = 3 x^{2} - 3 x - 18$

查看试题解析
5. 式子 $\overset{m 个 5}{\overset{︷}{\frac{5 \times 5 \times ⋯ \times 5}{\underset{n 个 9}{\underset{︸}{9 + 9 + ⋯ + 9}}}}}$ 可表示为（）

A、 $\frac{5 m}{9^{n}}$ B、 $\frac{5^{m}}{9 n}$ C、 $\frac{5 m}{n^{9}}$ D、 $\frac{m^{5}}{9 n}$

查看试题解析
6. 如果m是最大的负整数，那么1-m等于（）

A、-2 B、-1 C、0 D、2

查看试题解析

二、填空题（每小题3分，共24分）

7. 现实生活中，如果收入100元记作+100元，那么-700元表示.

查看试题解析
8. 比较大小： $- \frac{3}{5}$ $- \frac{3}{4}$ （填“<”或“>”）．

查看试题解析
9. 把数轴上表示数2的点移动5个单位后，表示的数为.

查看试题解析
10. 多项式 $2 + 3 x^{4} - 4 x^{2} y - x^{3} y + 6 x$ 按 $x$ 的降幂排列可以写成.

查看试题解析
11. 若单项式 $- 2 a^{2 m} b^{3}$ 与 $3 a^{2} b^{n - 1}$ 为同类项，则 $m - n =$ .

查看试题解析
12. 已知 $m^{2} - 2 m - 1 = 0$ ，则代数式 $m^{2} - 2 m + 3$ 的值为．

查看试题解析
13. 某校利用课后服务开展了主题为“书香满校园”的读书活动．现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为元．

查看试题解析
14. 如图所示，第1个图中将正方形取上下对边中点连线后，再取右侧长方形的长边中点
连线；第2个图中，将第一个图中的右下方正方形继续按第一个图的方式进行操作﹐…，
按此规律操作下去，则第n（n为正整数）个图形中正方形的个数是（用含n的代数式表示）.

查看试题解析

三、解答题（每15、16、17、18小题5分，共20分）

15. 计算： $|- 6|$ -7+（-3）

查看试题解析
16. 计算： $16 \div (- \frac{1}{2}) \times (- \frac{3}{8}) - (+ 4)$

查看试题解析
17. 计算： $- 18 \times (\frac{1}{2} - \frac{5}{6} + \frac{2}{3})$

查看试题解析
18. 计算： $- \frac{3}{4} \times [- 3^{2} \times {(- \frac{2}{3})}^{3} - 2]$

查看试题解析

四、解答题（每小题7分，共28分）

19. 如图，数轴上A，B，C，D，E分别表示–4.5，0，2，-2，- $\frac{1}{3}$
请回答下列问题：

(1)、在数轴上描出A，B，C，D，E五个点；

(2)、若把数轴的原点取在点C处，其余都不变，写出点D表示的数.

查看试题解析
20. 观察下列各式： $- a b ， - \frac{a}{2} ， \frac{2}{a} ， a + b ， a^{2} + a - 1$ .
回答下列问题：

(1)、单项式分别为：

(2)、多项式分别为：

(3)、整式有个；

(4)、-ab的系数为.

(5)、次数最高的多项式为

查看试题解析
21. 某果农把自家果园的柑橘包装后放到了抖音平台上销售．原计划每天卖10箱，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某个星期的销售情况（超额记为正，不足记为负，单位：箱）.

(1)、根据记录的数据可知前五天共卖出多少箱？

(2)、本周实际销售总量达到了计划数量没有？

查看试题解析
22. 如图，从一个长方形铁皮中剪去一个小正方形．

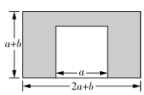(1)、请你用含有a，b的式子表示阴影部分的面积．

(2)、当a=7米，b=2米时，求阴影部分的面积．

查看试题解析

五、解答题（每小题8分，共16分）

23. 已知a，b在数轴上的位置如图所示：

(1)、用“>”、“<”或“=”填空：a0，a+b0，b-a0；

(2)、化简：la|+b–a|-2|a+b|：

(3)、若a=–2，b=1，x为数轴上任意一点所对应的数，则代数式|x–a|+|x-b|的最小值是.

查看试题解析
24. 探究规律，完成相关题目.
定义“*”运算：
$(+ 2) * (+ 4) = + (2^{2} + 4^{2}) ；$ $(- 4) * (- 7) = + [{(- 4)}^{2} + {(- 7)}^{2}]$
$(- 2) * (+ 4) = - [{(- 2)}^{2} + {(+ 4)}^{2}]$ ； $(+ 5) * (- 7) = - [{(+ 5)}^{2} + {(- 7)}^{2}]$
$0 * (- 5) = (- 5) * 0 = {(- 5)}^{2}$ ； $(+ 3) * 0 = 0 * (+ 3) = {(+ 3)}^{2}$
0*0=0²+0²=0

(1)、归纳*运算的法则：
两数进行*运算时，同号得正，.
特别地，0和任何数进行*运算，或任何数和О进行*运算，.
请把运算法则补充完整；

(2)、计算：（+1）*[0*（-2）]

(3)、若存在有理数m，n，使得（m-1）*（n+2）=0，请直接写出m，n的值.

查看试题解析

六、解答题（每小题10分，共20分）

25. 某公园有以下A，B，C三种购票方式：
种类购票方式
A 一次性使用门票，每张8元
B 年票每张80元，持票者每次进入公园无需再购买门票
C 年票每张40元，持票者进入公园时需再购买每次4元的门票

(1)、某游客一年中进入该公园共有a次，分别求三种购票方式一年的费用（用含a的代数式表示）；

(2)、某游客一年中进入该公园共有12次，选择哪种购买方式比较优惠？请说明理由；

(3)、已知甲，乙，丙三人分别按A，B，C三种方式购票，且他们一年中进入该公园的
次数相同．一年中，若甲所花的费用比乙和丙两人所花费用之和少60元，请直接写出甲一年中进入该公园的次数.

查看试题解析
26. 如图，将一条数轴在原点О和点B处各折一下，得到一条“折线数轴”．图中点A表示–8，点B表示8，点C表示14，我们称点A和点C在“折线数轴”上相距22个长度单位．动点P、Q同时出发，点Р从点A出发，以4单位/秒的速度沿着“折线数轴”的正方向运动，从点О运动到点B期间速度变为原来的四分之一，之后立刻恢复原速；动点Q从点C出发，以2单位/秒的速度沿着“折线数轴”的负方向运动，从点B运动到点О期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒，问：

(1)、当动点Р在OA上时，把点Р到点A的距离记为AP，则AP=（用t的代数式表示）；

(2)、当动点Р在OB上时，把点Р到点O的距离记为OP，则OP=用t的代数式表示）；

(3)、若动点Р运动的终点是点C，动点Q运动的终点是点A，动点P、Q是否同时到达终点，请说明理由；

(4)、当点Q在BC上时，Q、B两点在“折线数轴”上相距的长度与P、O两点在“折线数轴”上相距的长度相等时，t的值为(直接写出结果).

查看试题解析

种类	购票方式
A	一次性使用门票，每张8元
B	年票每张80元，持票者每次进入公园无需再购买门票
C	年票每张40元，持票者进入公园时需再购买每次4元的门票