四川省绵阳市2023年中考数学试卷

试卷更新日期：2024-02-22 类型：中考真卷

进入出卷网下载

一、选择题：本大题共12个小题，每小题3分，共36分．每个小题只有一个选项符合题要求．

1. 在实数0， $\frac{1}{2}$ ， ﹣π， $\sqrt{2}$ 中，最小的数是（　　）

A、﹣π B、0 C、 $\frac{1}{2}$ D、 $\sqrt{2}$

查看试题解析
2. 在2023年“五一”期间，仙海旅游景区接待游客102200人次，将102200用科学记数法表示为（　　）

A、1.022×10³ B、1.022×10⁴ C、1.022×10⁵ D、1.022×10⁶

查看试题解析
3. 下列几何体中三个视图完全相同的是（　　）

A、 B、 C、 D、

查看试题解析
4. 光线在不同介质中的传播速度是不同的，因此当光线从水中射向空气时，要发生折射，由于折射率相同，所以在水中平行的光线，在空气中也是平行的．如图， $∠ 1 = 122 ° ， ∠ 2$ 的度数为（）

A、 $32 °$ B、 $58 °$ C、 $68 °$ D、 $78 °$

查看试题解析
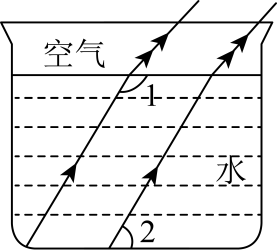5. 我国古代数学著作《孙子算经）中有“鸡兔同笼”问题：“今有鸡兔同笼，上有16头，下有44足，问鸡兔各几何．”设鸡x只，兔y只，可列方程组（　　）

A、 ${\begin{array}{l} x + y = 16 \\ 2 x + 4 y = 44 \end{array}$ B、 ${\begin{array}{l} x + y = 16 \\ 2 x + 2 y = 44 \end{array}$ C、 ${\begin{array}{l} x + y = 16 \\ 4 x + 4 y = 44 \end{array}$ D、 ${\begin{array}{l} x + y = 16 \\ 4 x + 2 y = 44 \end{array}$

查看试题解析
6. 蜜蜂的蜂巢美观有序，从入口处看，蜂巢由许多正六边形构成，则正六边形的对称轴有（　　）

A、4条 B、5条 C、6条 D、9条

查看试题解析
7. 阅读可以丰富知识，拓展视野，在世界读书日（4月23日）当天，某校为了解学生的课外阅读，随机调查了40名学生课外阅读册数的情况，现将调查结果绘制成如图．关于学生的读书册数，下列描述正确的是（　　）

A、极差是6 B、中位数是5 C、众数是6 D、平均数是5

查看试题解析
8. 如图，在等边△ABC中，BD是AC边上的中线，延长BC至点E，使CE＝CD，若DE＝ $4 \sqrt{3}$ ，则AB＝（　　）

A、 $4 \sqrt{3}$ B、6 C、8 D、 $8 \sqrt{3}$

查看试题解析
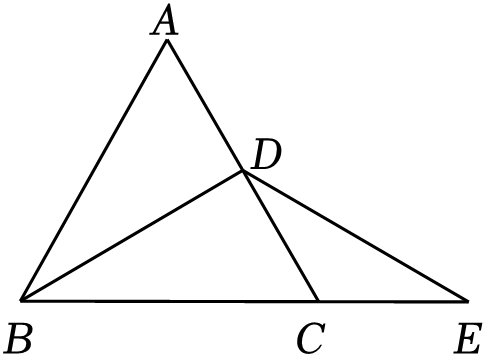9. 关于x的不等式组 ${\begin{array}{l} 3 x + 2 > m \\ \frac{x - 1}{2} ⩽ 1 \end{array}$ 有且只有两个整数解，则符合条件的所有整数m的和为（　　）

A、11 B、15 C、18 D、21

查看试题解析
10. 黄金分割由于其美学性质，受到摄影爱好者和艺术家的喜爱，摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，将正方形ABCD的底边BC取中点E，以E为圆心，线段DE为半径作圆，其与底边BC的延长线交于点F，这样就把正方形ABCD延伸为矩形ABFG，称其为黄金矩形．若CF＝4a，则AB＝（　　）

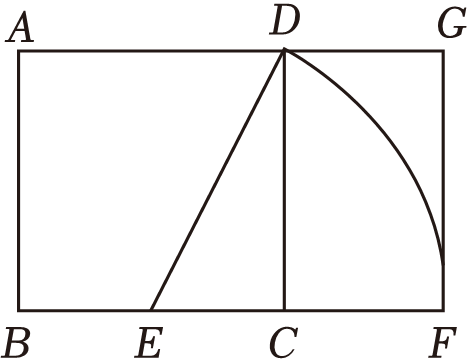A、（ $\sqrt{5}$ ﹣1）a B、（2 $\sqrt{5}$ ﹣2）a C、（ $\sqrt{5}$ +1）a D、（2 $\sqrt{5}$ +2）a

查看试题解析
11. 若x＝3是关于x的一元二次方程 $x^{2} - \frac{5}{3} a x - a^{2} = 0 (a > 0)$ 的一个根，下面对a的值估计正确的是（　　）

A、 $\frac{1}{2}$ ＜a＜1 B、1＜a＜ $\frac{3}{2}$ C、 $\frac{3}{2}$ ＜a＜2 D、2＜a＜ $\frac{5}{2}$

查看试题解析
12. 如图，在边长为4的正方形ABCD中，点G是BC上的一点，且BG＝3GC，DE⊥AG于点E，BF∥DE，且交AG于点F，则tan∠EDF的值为（　　）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{2}{5}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题：本大题共6个小题，每小题4分，共24分．将答案填写在答题卡相应的横线上．

13. 因式分解：x²﹣9x＝．

查看试题解析
14. 在平面直角坐标系中，将点A（﹣1，2）先向右平移1个单位，再向下平移2个单位，得到点B（a，b），则a+b＝．

查看试题解析
15. 若式子 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x的最小值为．

查看试题解析
16. 如图，厂房屋顶人字架（等腰三角形）的跨度BC＝10m，∠B＝30°，则中柱AD（D为底边中点）的长为 m．

查看试题解析
17. 随着国家提倡节能减排，新能源车将成为时代“宠儿”．端午节，君君一家驾乘新购买的新能源车，去相距180km的古镇旅行，原计划以速度v km/h匀速前行，因急事以计划速度的1.2倍匀速行驶，结果就比原计划提前了0.5h到达，则原计划的速度v为 km/h．

查看试题解析
18. 如图，在△ABC中，∠ACB＝90°，AC＝8，将△ABC绕点C按逆时针方向旋转得到△A₁B₁C，满足A₁B₁∥AC，过点B作BE⊥A₁C，垂足为E，连接AE，若S_△_ABE＝3S_△_ACE ，则AB的长为．

查看试题解析

三、解答题：本大题共7个小题，共90分．解答应写出文字说明、证明过程或演算步骤．

19.

(1)、计算： $\sqrt{12} - 4 | Unsupported character s i n 6 0^{°} | + {(\frac{1}{3})}^{- 1} - (2023 - π)^{0}$ ；

(2)、先化简，再求值： $(1 + \frac{3}{x - 5}) \div \frac{x^{2} - 4 x + 4}{2 x - 10}$ ，其中 $x = \sqrt{2} + 2$

查看试题解析
20. 随着科技的进步，购物支付方式日益增多．为了解某社区居民支付的常用方式（A微信，B支付宝，C现金，D其他），某学习小组对红星社区部分居民进行问卷调查，根据查结果，绘制成如图统计图．
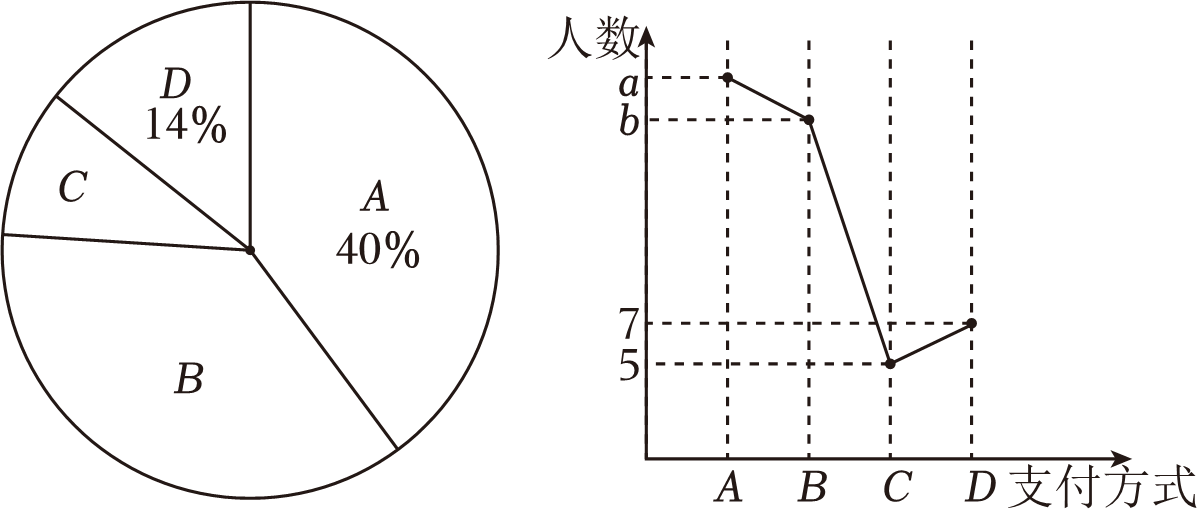
根据统计图表中的信息，解答下列问题：

(1)、a＝， b＝，在扇形统计图中C种支付方式所对应的圆心角为度；

(2)、本次调查中用现金支付方式的居民里有2名男性，其余都是女性，现从该种支付方式中随机选2名居民参加线上支付方式培训，求恰好都是女性的概率．

查看试题解析
21. 随着国家乡村振兴政策的推进，凤凰村农副产品越来越丰富．为增加该村村民收入，计划定价销售某土特产，他们把该土特产（每袋成本10元）进行4天试销售，日销量y（袋）和每袋售价x（元）记录如下：
时间
第一天
第二天
第三天
第四天
x/元
15
20
25
30
y/袋
25
20
15
10
若试销售和正常销售期间，日销量y与每袋售价x的一次函数关系相同，解决下列问题：

(1)、求日销量y关于每袋售价x的函数关系式；

(2)、请你帮村民设计，每袋售价定为多少元，才能使这种土特产每日销售的利润最大？并求出最大利润．（利润＝销售额﹣成本）

查看试题解析
22. 如图，▱ABCD的对角线AC，BD相交于点O，点E，F在AC上，且AE＝CF．

(1)、求证：BE∥DF；

(2)、过点O作OM⊥BD，垂足为O，交DF于点M，若△BFM的周长为12，求四边形BEDF的周长．

查看试题解析
23. 如图，过原点O的直线与反比例函数 $y_{1} = \frac{k}{x}$ （k≠0）的图象交于A（1，2），B两点，一次函数y₂＝mx+b（m≠0）的图象过点A与反比例函数交于另一点C（2，n）．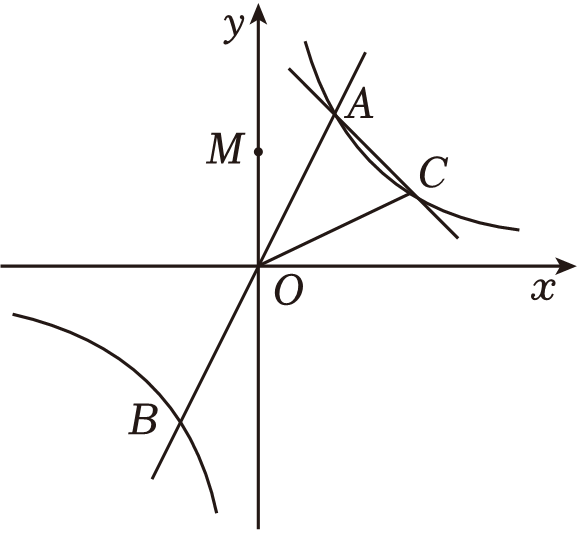

(1)、求反比例函数的解析式；当y₁＞y₂时，根据图象直接写出x的取值范围；

(2)、在y轴上是否存在点M，使得△COM为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．

查看试题解析
24. 如图，在⊙O中，点A，B，C，D为圆周的四等分点，AE为切线，连接ED．并延长交⊙O于点F，连接BF交AC于点G．

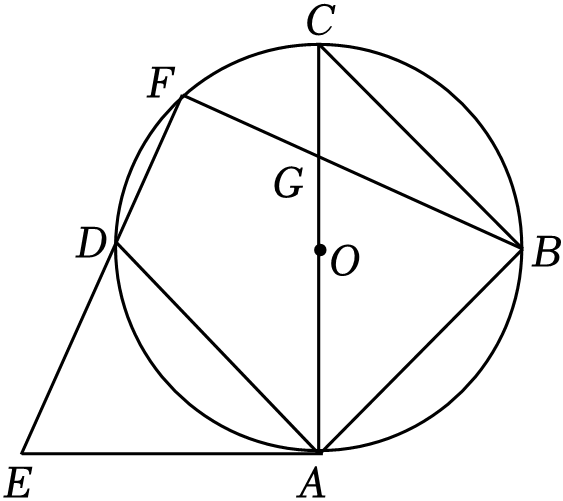(1)、求证：AD平分∠CAE；

(2)、求证：△ADE≌△ABG；

(3)、若AE＝3，AG＝3GC，求cos∠CBF的值．

查看试题解析
25. 如图，抛物线经过△AOD的三个顶点，其中O为原点，A（2，4），D（6，0），点F在线段AD上运动，点G在直线AD上方的抛物线上，GF∥AO，GE⊥DO于点E，交AD于点I，AH平分∠OAD，C（﹣2，﹣4），AH⊥CH于点H，连接FH．

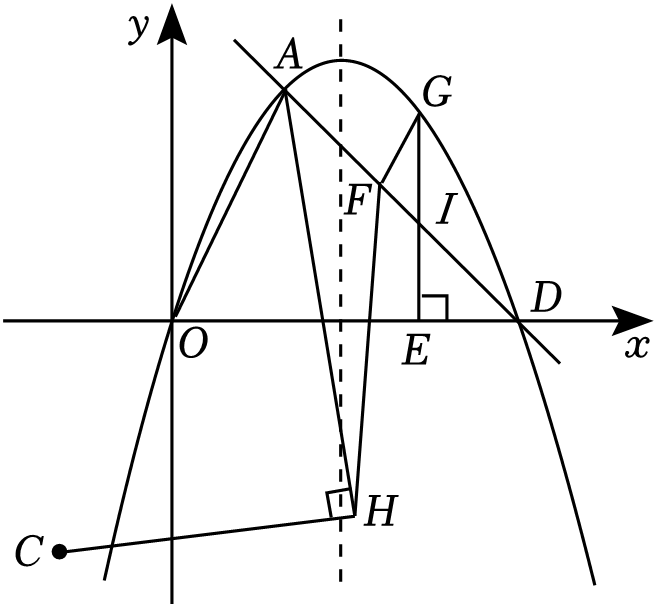(1)、求抛物线的解析式及△AOD的面积；

(2)、当点F运动至抛物线的对称轴上时，求△AFH的面积；

(3)、试探究 $\frac{F G}{G I}$ 的值是否为定值？如果为定值，求出该定值；不为定值，请说明理由．

查看试题解析

时间	第一天	第二天	第三天	第四天
x/元	15	20	25	30
y/袋	25	20	15	10