（华师大版）2023-2024学年度第二学期八年级数学18.1 平行四边形的性质 同步测试
试卷更新日期：2024-02-22 类型：同步测试
一、选择题
-
1. 如图，在中， ， 则（ ）
A、30° B、50° C、60° D、120°2. 如图，平行四边形的对角线 ， 交于点 ， 已知 ， ， 的周长为15，则的长为（ ）
A、5 B、6 C、7 D、83. 如图，在▱ABCD中，过点 D作 DE⊥AB，垂足为E，过点 B 作 BF⊥AC，垂足为 F.若 AB =6，AC=8，DE=4，则BF的长为 （ ）
A、4 B、3 C、 D、24. 如图所示，▱ABCD的对角线AC，BD相交于点O，AE=EB，OE=3，AB=5，▱ABCD的周长（ ）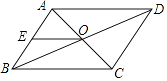
A、11 B、13 C、16 D、225. 如图，在▱ABCD中，对角线AC，BD相交于点O，OE⊥BD交 AD 于点E，连结 BE.若▱ABCD的周长为 28，则△ABE的周长为 （ ）
A、28 B、24 C、21 D、146. 如图，在ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE，若∠COE= 35°，∠ADC=45°，则∠BAC=（ ）
A、70° B、90° C、100° D、110°7. 在中，若的度数是（ ）A、 B、 C、 D、8. 如图，在中， ， ， 点D在边上，以 ， 为边作平行四边形 ， 则的度数为（ ）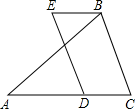
A、 B、 C、 D、9. 如图，在平行四边形中，对角线 ， 分别以点为圆心，以大于的长为半径画弧，两弧相交于点和点 ， 作直线 ， 交对角线于点 ， 连接恰好垂直于边 ， 若 ， 则的长是（ ）
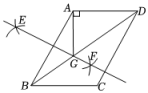A、6 B、8 C、1 D、110. 如图，A是反比例函数 的图象上任意一点，AB∥x轴，交反比例函数 的图象于点B，以AB为边作□ABCD，其中点C，D在x轴上，则 S▱ABCD等于 （ ）
A、2.5 B、3 C、5 D、6二、填空题
-
11. 如图，ABCD的对角线AC，BD相交于点O，且AC+BD=26，AB=8，则△OCD的周长是.
12. 如图，在▱ABCD 中，若∠A=2∠B，则∠D=°.
13. 如图，四边形ABCD 是平行四边形，点D 的纵坐标是6，CD=10，顶点A在y轴上，边 BC 在x轴上.设 P 是射线 BC上的一个动点，则当△ABP 为等腰三角形时，点P的坐标是.
14. 如图，▱ABCD的边BC=6，对角线AC，BD相交.于点O，△OAB 的周长比△OBC的周长大3，则AB=.
15. 已知在▱ABCD中，∠ABC 和∠BCD的平分线分别交直线AD 于点 E，F，AB=5.若 EF>4，则AD的取值范围是.三、解答题
-
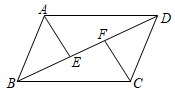
16. 如图，O为▱ABCD的对角线AC 的中点，过点O 作直线 MN，分别交边 AB，CD 于点 M，N，点E，F 在直线MN上，OE=OF，连结AE，CF.
(1)、求证：∠EAM=∠FCN.(2)、写出图中所有的全等三角形.17. 已知：如图， 、 是平行四边形 对角线 上两点， ．求证： ．
