备考2024年高考数学提升专题特训：等式与不等式

试卷更新日期：2024-02-22 类型：三轮冲刺

进入出卷网下载

一、解答题

1.

(1)、已知 $1 < a < 6$ ， $3 < b < 4$ ，求 $2 a - b$ ， $\frac{a}{b}$ 的取值范围

(2)、已知 $a ， b ， x ， y \in (0 ， + \infty)$ ，且 $\frac{1}{a} > \frac{1}{b}$ ， $x > y$ ，试比较 $\frac{x}{x + a}$ 与 $\frac{y}{y + b}$ 的大小.

查看试题解析
2.

(1)、已知实数x ， y满足 $- 2 \leq x \leq - 1$ ， $2 \leq y \leq 3$ ，求 $3 x - 2 y$ 的取值范围；

(2)、已知实数 $x > 1$ ，求 $x + \frac{2}{x - 1}$ 的最小值.

查看试题解析
3.

(1)、设 $x ， y \in R$ ，用反正法证明：若 $x + y > 2$ ，则 $x > 1$ 或 $y > 1$

(2)、设 $a \in R$ ，比较 ${(a + 1)}_{}^{2}$ 与 $a_{}^{2} - a + 1$ 的值的大小

查看试题解析
4. 对于函数 $f (x)$ ，若在定义域内存在实数x ，满足 $f (- x) = f (x)$ ，则称 $f (x)$ 为“局部偶函数”，

(1)、已知函数 $f (x) = x^{3} + x + 1$ ，试判断 $f (x)$ 是否为“局部偶函数”，并说明理由；

(2)、若 $f (x) = x [4^{x} + (2 m - 1) \cdot 2^{x} + 3]$ 为定义在区间 $(- \infty ， 0) \cup (0 ， + \infty)$ 上的“局部偶函数”，求实数m的取值范围.

查看试题解析
5. 在 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $2 a c s i n (B + C) + a^{2} + c^{2} - b^{2} = 0$ .

(1)、若 $A = \frac{π}{6}$ ， $a = 2$ ，求 $△ A B C$ 的面积；

(2)、求 $\frac{4 s i n^{2} C + 3 s i n^{2} A + 2}{s i n^{2} B}$ 的最小值，并求出此时 $B$ 的大小.

查看试题解析
6. 已知直线 $l ： a x - y - 3 + a^{2} = 0 (a \in R)$ .

(1)、若 $l$ 不经过第三象限，求 $a$ 的取值范围；

(2)、求坐标原点 $O$ 到直线 $l$ 距离的最小值，并求此时直线 $l$ 的方程.

查看试题解析
7. 对于函数 $f (x)$ 和 $g (x)$ ，记函数 $f (x)$ 的定义域为 $A$ ，函数 $g (x)$ 的定义域为 $B$ ，若 $B ⊆ A$ ，则称函数 $g (x)$ 是函数 $f (x)$ 的好函数，否则，称函数 $g (x)$ 不是函数 $f (x)$ 的好函数.现已知函数 $h (x)$ 的定义域为 $(0 ， + \infty)$ .

(1)、若函数 $φ (x) = h (2 x - 1)$ ，判断函数 $φ (x)$ 是不是函数 $h (x)$ 的好函数；

(2)、若函数 $u (x) = h (- x^{2} - a x + a + 1)$ ，且函数 $u (x)$ 是函数 $h (x)$ 的好函数，求实数 $a$ 的取值范围.

查看试题解析
8.

(1)、若 $a x^{2} + 2 a x - 1 < 0$ 对一切 $x \in R$ 恒成立，求实数 $a$ 的取值范围；

(2)、求关于 $x$ 的不等式 $x^{2} + a x - a \geq 0$ 的解集.

查看试题解析
9. 已知函数 $f (x) = x^{2} - (a + 1) x + 1 (a \in R)$

(1)、若不等式 $f (x) < 1 - b$ 的解集为 ${x | - 1 < x < 3}$ ，求 $a ， b$ 的值；

(2)、若对任意的 $x \in [2 ， 4] ， f (x) + a + 3 \geq 0$ 恒成立，求实数 $a$ 的取值范围

(3)、已知 $g (x) = m x + 1 - 2 m$ ，当 $a = 1$ 时，若对任意的 $x_{1} \in [1 ， 4]$ ，总存在 $x_{2} \in [1 ， 4]$ ，使 $f (x_{1}) = g (x_{2})$ 成立，求实数 $m$ 的取值范围．

查看试题解析
10. 某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物，6个单位的蛋白质和6个单位的维生素 $C$ ；一个单位的晚餐含8个单位的碳水化合物，6个单位的蛋白质和10个单位的维生素 $C$ .另外，该儿童这两餐需要的营养中至少含64个单位的碳水化合物，42个单位的蛋白质和54个单位的维生素 $C$ .如果一个单位的午餐、晚餐的费用分别是2.5元和4元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐?

查看试题解析
11. 某企业生产甲、乙两种产品均需用 $A ， B$ 两种原料.已知生产1吨每种产品需原料及每天原料的可用限额如表所示：

(1)、设该企业每天生产甲、乙两种产品分别为 $x ， y$ 吨，试写出关于 $x ， y$ 的线性约束条件并画出可行域；

(2)、如果生产1吨甲、乙产品可获利润分别为3万元、4万元，试求该企业每天可获得的最大利润.

查看试题解析

12. 某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载新产品A、B，要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：

	产品A(件)	产品B(件)
研制成本与塔载费用之和(万元/件)	20	30	计划最大资金额300万元
产品重量(千克/件)	10	5	最大搭载重量110千克
预计收益(万元/件)	80	60

试问：如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？

查看试题解析

13. 已知函数 $f (x)$ 的定义域为R ，值域为 $(0 ， + \infty)$ ，且对任意m ， $n \in R$ ，都有 $f (m + n) = f (m) f (n)$ ， $φ (x) = \frac{f (x) - 1}{f (x) + 1}$ .

(1)、求 $f (0)$ 的值，并证明 $φ (x)$ 为奇函数；

(2)、当 $x > 0$ 时， $f (x) > 1$ ，且 $f (3) = 4$ ，证明 $f (x)$ 为R上的增函数，并解不等式 $φ (x) > \frac{15}{17}$

查看试题解析
14. 已知函数 $f (x) = | 4 x + a | - | 4 x + a^{2} |$ ．

(1)、若 $a = 2$ ，求不等式 $f (x) + \frac{1}{2} x < 1$ 的解集；

(2)、若 $\exists x \in R$ ， $\exists a \in [0 ， 2]$ ，使得 $f (\frac{1}{2} x) > m$ 能成立，求实数m的取值范围．

查看试题解析
15. 已知函数 $f (x) = 2 l n x + \frac{(k - 1) (x^{2} - 1)}{x} ， k \in R$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、证明： $l n (n + 1) < \frac{1}{2} + \frac{1}{3} + ⋯ + \frac{1}{n} + \frac{n + 2}{2 (n + 1)}$ （ $n \in N^{*}$ ， $n \geq 2$ ）.

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} x + 6 ， x \leq 0 \\ x^{2} - 2 x + 2 ， x > 0 \end{array}$ .

(1)、求不等式 $f (x) > 5$ 的解集；

(2)、若方程 $f (x) - \frac{m^{2}}{2} = 0$ 有三个不同实数根，求实数 $m$ 的取值范围．

查看试题解析
17. 已知函数 $f (x)$ 的定义域为R，对任意实数x，y， $f (x + y) = f (x) + f (y) + 2$ ．当 $x > 0$ 时， $f (x) < - 2$ ， $f (1) = - 6$ ．

(1)、求 $f (0)$ ， $f (- 1)$ 的值；

(2)、判断函数 $f (x)$ 的单调性并加以证明；

(3)、解不等式 $f (x^{2}) - f (x + \frac{7}{4}) > 4$ ．

查看试题解析
18. 已知函数 $f (x) = a^{x} + b$ （ $a > 0$ ，且 $a \neq 1$ ）的部分图象如图所示.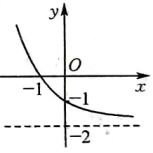

(1)、求 $f (x)$ 的解析式；

(2)、若关于 $x$ 的不等式 ${(\frac{1}{a})}^{x} + (- 2 b)^{x} - m \leq 0$ 在 $[1 ， + \infty)$ 上有解，求实数 $m$ 的取值范围.

查看试题解析
19. 秋冬季是流感的高发季节，为了预防流感，东竞高中决定对教室采用药熏消毒法进行消毒，药熏开始前要求学生全部离开教室.已知在药熏过程中，教室内每立方米空气中的药物含量 $y$ (毫克) 与药熏时间 $t$ (小时) 成正比：当药熏过程结束，药物即释放完毕，教室内每立方米空气中的药物含量 $^{y}$ (毫克) 达到最大值.此后，教室内每立方米空气中的药物含量 $^{y}$ (毫克) 与时间 $t$ (小时) 的函数关系式为 $y = {(\frac{1}{16})}^{t - a}$ ( $a$ 为常数， $t > \frac{1}{2}$ ). 已知从药熏开始，教室内每立方米空气中的药物含量 $y$ (毫克) 关于时间 $t$ (小时) 的变化曲线如图所示.

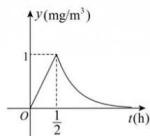(1)、从药熏开始，求每立方米空气中的药物含量 $y$ (毫克) 与时间 $t$ (小时) 之间的函数关系式；

(2)、据测定，当空气中每立方米的药物含量不高于 $\frac{1}{4}$ 毫克时，学生方可进入教室，那么从药薰开始，至少需要经过多少小时后，学生才能回到教室.

查看试题解析
20. 候鸟每年都要随季节的变化而进行大规模地迁徙，研究某种鸟类的专家发现，该种鸟类的飞行速度v(单位：m/s)与其耗氧量M之间的关系为 $v = a + b l o g_{2} \frac{M - 25}{10}$ （其中a，b是常数），据统计，该种鸟类在静止时其耗氧量为65个单位，而其耗氧量为105个单位时，其飞行速度为1 m/s.

(1)、求 $202 0^{1 + a} + l o g_{2020} b$ 的值；

(2)、若这种鸟类为赶路程，飞行的速度不能低于3 m/s，则其耗氧量至少要多少个单位?

查看试题解析
21. 已知函数 $f (x) = x^{2} - (a + \frac{1}{a}) x + 1 (x \in R)$ ．

(1)、当 $a = 3$ 时，求不等式 $f (x) < 0$ 的解集；

(2)、若关于 $x$ 的不等式 $f (x) < 0$ 有且仅有2个整数解，求正实数a的取值范围．

查看试题解析
22. 已知函数 $f (x) = \frac{a x}{e^{x}} (a \neq 0)$ .

(1)、求函数 $f (x)$ 的单调区间；

(2)、当 $a = 1$ 时，如果方程 $f (x) = t$ 有两个不等实根 $x_{1} ，$ $x_{2}$ ，求实数t的取值范围，并证明 $x_{1} + x_{2} > 2$ .

查看试题解析
23. 如图所示，将一矩形花坛 $A B C D$ 扩建成一个更大的矩形花坛 $A M P N$ ，要求 $B$ 点在 $A M$ 上， $D$ 点在 $A N$ 上，且对角线 $M N$ 过 $C$ 点.已知AB=3米，AD=2米.

(1)、要使矩形 $A M P N$ 的面积大于32平方米，请问 $A N$ 的长应在什么范围；

(2)、当 $A N$ 的长度是多少时，矩形 $A M P N$ 的面积最小，并求出最小面积.

查看试题解析