湖南省娄底市双峰县2023-2024学年七年级上学期月考数学试题

试卷更新日期：2024-02-22 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30分．在每小题列出的选项中，选出符合题目的一项）

1. 如果温度上升5℃，记作 $+ 5$ ℃，那么温度下降 $2$ ℃记作（）

A、 $+ 2$ ℃ B、 $- 2$ ℃ C、 $+ 3$ ℃ D、 $- 3$ ℃

查看试题解析
2. 与 $- \frac{1}{4} a b$ 是同类项的为（）

A、2abc B、 $2 a b^{2}$ C、ab D、 $\frac{1}{2}$

查看试题解析
3. 将代数式 $- 2 (x - 3 y + 1)$ 去括号后，得到的正确结果是（）

A、 $- 2 x + 3 y - 1$ B、 $- 2 x - 6 y + 2$ C、 $- 2 x + 6 y - 2$ D、 $- 2 x + 5 y - 2$

查看试题解析
4. 用含有字母的式子表示下列数量关系“a的3倍与b的差的平方”，正确的是（）

A、 $3 a - b^{2}$ B、 ${(3 a - b)}^{2}$ C、 $3 {(a - b)}^{2}$ D、 ${(a - 3 b)}^{2}$

查看试题解析
5. 已知x=2是关于x的一元一次方程mx+2=0的解，则m的值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
6. 2023年全国高考报名人数约12910000人，数12910000用科学记数法表示为（）

A、 $0.1291 \times 1 0^{8}$ B、 $1.291 \times 1 0^{7}$ C、 $1.291 \times 1 0^{8}$ D、 $12.91 \times 1 0^{7}$

查看试题解析
7. 已知 $x + y = - 1010$ ，则代数式 $3 - 2 x - 2 y$ 的值为（）

A、2023 B、 $- 2021$ C、2021 D、 $- 2023$

查看试题解析
8. 如图所示，数轴上标出若干个点，每相邻两点相距一个单位长度，点A，B，C，D对应的数分别是数a，b，c，d，且d-2a=10，那么数轴的原点应是（）

A、A点 B、B点 C、C点 D、D点

查看试题解析
9. 已知8个长为a，宽为b的小长方形（如图1），不重叠无空隙地摆放（如图2），在长方形ABCD中，当BC长度变化时，左上角阴影面积 $S_{1}$ 与右下角阴影面积 $S_{2}$ 的差没有变化，则a，b之间的关系应满足（）

A、 $5 b = 2 a$ B、 $3 b = a$ C、 $2 b = a$ D、 $5 b = 3 a$

查看试题解析
10. 我国古代数学名著《算法统宗》中，有一道“群羊逐草”的问题，大意是：牧童甲在草原上放羊，乙牵着一只羊来，并问甲：“你的羊群有100只吗？”甲答：“如果在这群羊里加上同样的一群，再加上半群，四分之一群，再加上你的一只，就是100只．”问牧童甲赶着多少只羊？若设这群羊有x只，则下列方程中，正确的是（　　）

A、（1+ $\frac{1}{2}$ + $\frac{1}{4}$ ）x=100+1 B、x+x+ $\frac{1}{2}$ x+ $\frac{1}{4}$ x=100﹣1 C、（1+ $\frac{1}{2}$ + $\frac{1}{4}$ ）x=100﹣1 D、x+x+ $\frac{1}{2}$ x+ $\frac{1}{4}$ x=100+1

查看试题解析

二、填空题（本大题共6小题，共18分）

11. a与1互为相反数，那么a= ．

查看试题解析
12. 单项式 $3 x y$ 的系数为．

查看试题解析
13. 如图，经过刨平的木板上的A，B两个点，可以弹出一条笔直的墨线，能解释这一实际应用的数学知识是 .

查看试题解析
14. 已知线段 $A B = 6$ ，延长AB至点C，使 $B C = \frac{1}{3} A B$ ，反向延长AC至点D，使 $A D = \frac{1}{2} A C$ ，则CD的长为．

查看试题解析
15. 某种商品每件的进价为120元，标价为180元．为了拓展销路，商店准备打折销售．若使利润率为20%，则商店应打折．

查看试题解析
16. 按照如图所示的方法排列黑色小正方形地砖，则第100个图案中黑色小正方形地砖的块数是．

查看试题解析

三、计算题（本大题共3小题，共18分）

17. 计算： $- 1^{4} - | 0.5 - 1 | \times 2 - (- 3)^{2} \div (- \frac{3}{2})$

查看试题解析
18. 如图，有理数a，b，c在数轴上，且 $| a | = | b |$ ．

(1)、判断正负（用“<”，“>”或“=”填空）： $b - c$ 0； $a + b$ 0； $a + c$ 0．

(2)、化简： $| b - c | + | a + b | - | a + c |$ ．

查看试题解析
19. 已知多项式 $2 x^{2} + m y - 12$ 与多项式 $n x^{2} - 3 y + 6$ 的差中不含有 $x$ ， $y$ ，求 $m + n + m n$ 的值．

查看试题解析

四、解答题（每小题8分，共16分）

20. 解方程：

(1)、 $4 x - 3 (4 - x) = 2$ ；

(2)、 $\frac{2 x - 1}{6} - \frac{5 x + 1}{4} = 1$ ．

查看试题解析
21. 化简并求值： $2 (\frac{1}{2} x^{2} - 3 x y - y^{2}) - (x^{2} - 5 x y - 2 y^{2})$ ，其中 $x = 2 ， y = 1$ .

查看试题解析

五、解答题（每小题9分，共18分）

22. 如图，点B是线段AC上一点，且 $A B = 21$ ， $B C = \frac{1}{3} A B$ ．

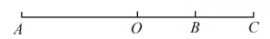(1)、求线段AC的长．

(2)、若点O是线段AC的中点，求线段OB的长．

查看试题解析
23. 甲，乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价40元，乒乓球每盒定价5元.而甲，乙两店的促销方案不同，甲店每买一副球拍赠送一盒乒乓球，乙店全部按定价的九折优惠.该班需球拍5副，乒乓球若干盒（不小于5盒）.

(1)、当购买乒乓球多少盒时，两种优惠办法付款一样？

(2)、若购买15盒乒乓球时，请你去办这件事，你打算去哪一家商店购买？为什么？

查看试题解析

六、综合题（每小题10分，共20分）

24. 阅读材料：
我们定义：如果两个实数的和等于这两个实数的积，那么这两个实数就叫做“和积等数对”，即：如果 $a + b = a \times b$ ，那么a与b就叫做“和积等数对”，记为 $(a ， b)$ .
例如： $2 + 2 = 2 \times 2$ ， $\frac{1}{2} + (- 1) = \frac{1}{2} \times (- 1)$ ， $3 + \frac{3}{2} = 3 \times \frac{3}{2}$ ，
则称数对 $(2 ， 2)$ ， $(\frac{1}{2} ， - 1)$ ， $(3 ， \frac{3}{2})$ 是“和积等数对”.
根据上述材料，解决下列问题：

(1)、下列数对中，“和积等数对”是 $($ 填序号 $)$ ；
① $(- \frac{2}{3} ， 2)$ ； ② $(\frac{5}{4} ， 5)$ ； ③ $(- 1 ， 2)$ .

(2)、如果 $(x ， 4)$ 是“和积等数对”，请求出x的值；

(3)、如果 $(m ， n)$ 是“和积等数对”，那么m=（用含 $n$ 的代数式表示）.

查看试题解析
25. 已知 $x = - 3$ 是关于x的方程 $(k + 3) x + 2 = 3 x - 2 k$ 的解．

(1)、求k的值；

(2)、在（1）的条件下，已知线段 $A B = 6 c m$ ，点C是线段AB上一点，且 $B C = k A C$ ，若点D是AC的中点，求线段CD的长．

(3)、在（2）的条件下，已知点A所表示的数为-2，点B所表示的数为4，有一动点P从点A开始以2个单位长度每秒的速度沿数轴向左匀速运动，同时另一动点Q从点B开始以4个单位长度每秒的速度沿数轴向左匀速运动，当时间为多少秒时，有 $P D = 2 Q D$ ？

查看试题解析