湖南省长沙市五校联考2023-2024学年九年级上学期月考数学试题

试卷更新日期：2024-02-22 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30分。在每小题列出的选项中，选出符合题目的一项）

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 月球沿着一定的轨道围绕地球运动，它的半长轴约为385000千米，这个数据用科学记数法精确到万位表示，应记为（）千米.

A、 $3.85 \times 1 0^{5}$ B、 $3.9 \times 1 0^{5}$ C、 $38.5 \times 1 0^{4}$ D、 $0.39 \times 1 0^{6}$

查看试题解析
3. 下列各数中的无理数是（）

A、 $\sqrt{4}$ B、 $π$ C、0 D、 $- \frac{22}{7}$

查看试题解析
4. 从正三角形、正方形、正五边形、正六边形中任选一个，选中的恰好既是轴对称图形，又是中心对称图形的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
5. 用反证法证明“若ab＝0，则a，b中至少有一个为0”时，第一步应假设（）

A、a＝0，b＝0 B、a≠0，b≠0 C、a≠0，b＝0 D、a＝0，b≠0

查看试题解析
6. 下列命题中，假命题是（）

A、平行四边形的对角线相等 B、正方形的对角线互相垂直平分 C、对角线互相垂直的平行四边形是菱形 D、有一个角为 $90 °$ 的平行四边形是矩形

查看试题解析
7. 如图，在扇形AOB中，D为弧AB上的点，连接AD并延长与OB的延长线交于点C，若CD＝OA，∠O＝69°，则∠A的度数为（）

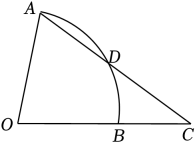A、35° B、52.5° C、70° D、74°

查看试题解析
8. 如图，在平面直角坐标系中，已知点A，B的坐标分别为 $(- 3 ， 1)$ ， $(- 1 ， 4)$ .以点O为位似中心，在原点的另一侧按2∶1的相似比将 $△ O A B$ 缩小，则点A的对应点 $A^{'}$ 的坐标是（）

A、 $(- 3 ， 1)$ B、 $(- \frac{3}{2} ， \frac{1}{2})$ C、 $(3 ， - 1)$ D、 $(\frac{3}{2} ， - \frac{1}{2})$

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 与 $⊙ O$ 的相切，与 $A B$ 的延长线相交于点C，若 $∠ C = 26 °$ ，那么 $∠ A$ 为（）

A、26° B、27° C、32° D、37°

查看试题解析
10. 《孙子算经》是中国古代重要的数学著作，成书大约在一千五百年前.其中一道题，原文是：“今三人共车，两车空；二人共车，九人步.问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车：若每辆车乘坐2人，则有9人步行，问人与车各多少？设有 $x$ 人， $y$ 辆车，可列方程组为（）

A、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x}{2} + 9 = y \end{array}$ B、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x - 9}{2} = y \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x - 9}{2} = y \end{array}$ D、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x}{2} - 9 = y \end{array}$

查看试题解析

二、填空题（本大题共6小题，共18分）

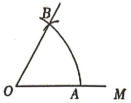
11. 一个不透明的袋中装有3个红球和2个白球，这些球除颜色外无其他差别.现随机从袋中摸出一个球，这个球是白球的概率是.

查看试题解析
12. 若 $\sqrt{x - 8}$ 在实数范围内有意义，则实数x的取值范围是．

查看试题解析
13. 平面直角坐标系中，点A（2，3）关于x轴的对称点坐标为．

查看试题解析
14. 如图，以点O为圆心，任意长为半径画弧，与射线 $O M$ 交于点A，再以点A为圆心， $A O$ 长为半径画弧，与前弧交于点B，画出射线 $O B$ ，则 $∠ A O B$ 的度数.

查看试题解析
15. 如图所示，点B是反比例函数 $y = \frac{k}{x}$ 图象上的一点，过点B作x轴的垂线，垂足为A，连接 $O B$ ，若 $△ A O B$ 的面积是4，则反比例函数的解析式是.

查看试题解析
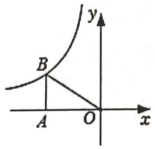16. 如图，正方形 $A B C D$ 的边长为4，点E是正方形外一动点，且点E在 $C D$ 的右侧， $∠ A E D = 45 °$ ， P为 $A B$ 的中点，当E运动时，线段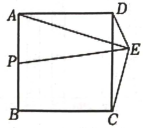 $P E$ 的最大值为.

查看试题解析

三、解答题（解答应写出文字说明，证明过程或演算步骤）

17. 计算： $- 3^{2} - | - 2 | + (- 1)^{100}$ .

查看试题解析
18. 先化简，再求值： $\frac{a - 1}{a} \div (a - \frac{1}{a})$ ，其中 $a = 2023$ ．

查看试题解析
19. 某学校要开展校园文化艺术节活动，为了合理编排节目，对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查（每名学生必须选择且只能选择一类），并将调查结果绘制成如下不完整统计图.
请你根据图中信息，回答下列问题：

(1)、本次共调查了名学生.

(2)、补全条形统计图（标注频数）.

(3)、九年一班和九年二班各有2名学生擅长舞蹈，学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排，那么抽取的2名学生恰好来自同一个班级的概率是多少？

查看试题解析
20. 如图，在平行四边形 $A B C D$ 中，E为 $D C$ 边上一点， $∠ E A B = ∠ E B C$ .

(1)、求证： $△ A B E ~ △ B E C$ ；

(2)、若 $B E = 2$ ，求 $C D \cdot C E$ 的值.

查看试题解析
21. 如图，已知矩形 $O A B C$ 的两边 $O A$ 、 $O C$ 分别落在x轴、y轴的正半轴上，顶点B的坐标是 $(6 ， 4)$ ，反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象经过矩形对角线的交点E，且与 $B C$ 边交于点D.

(1)、求反比例函数的解析式与点D的坐标；

(2)、求出 $△ O D E$ 的面积；

查看试题解析
22. 某商场销售A、B两种商品，每件进价均为20元.调查发现，如果售出4种20件，B种10件，销售总额为840元；如果售出A种10件，B种15件，销售总额为660元.

(1)、求A、B两种商品的销售单价；

(2)、经市场调研，A种商品按原售价销售，可售出40件，原售价每降价1元，销售量可增加10件；B种商品的售价不变，A种商品售价不低于B种商品售价.设A种商品降价m元，如果A、B两种商品销售量相同，求m取何值时，商场销售A、B两种商品可获得总利润最大？最大利润是多少？

查看试题解析
23. 如图， $A B$ 是 $⊙ O$ 的直径， $C$ ， $D$ 都是 $⊙ O$ 上的点，且 $A D$ 平分 $∠ C A B$ ，过点 $D$ 作 $A C$ 的垂线交 $A C$ 的延长线于点 $E$ ，交 $A B$ 的延长线于点 $F$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、若 $A B = 13$ ， $A C = 5$ ，求 $C E$ 的长．

查看试题解析
24. 如图1， $⊙ l$ 与直线相离a，过圆心l作直线a的垂线，垂足为H，且交 $⊙ l$ 于P，Q两点（Q在P，H之间）.我们把点P称为 $⊙ l$ 关于直线a的“远点”，把 $P Q \cdot P H$ 的值称为 $⊙ l$ 关于直线a的“特征数”.

图1    图2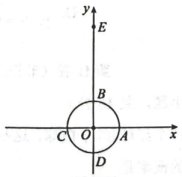

(1)、如图2，在平面直角坐标系 $x O y$ 中，点的坐标为 $(0 ， 4)$ ，半径为1的 $⊙ O$ 与两坐标轴交于点A，B，C，D.
①过点E作垂直于y轴的直线m，则 $⊙ O$ 关于直线m的“远点”是点    ▲        （填“A”，“B”，“C”或“D”）， $⊙ O$ 关于直线m的“特征数”为    ▲        ；
②若直线n的函数表达式为 $y = \sqrt{3} x + 4$ ，求 $⊙ O$ 关于直线n的“特征数”；

(2)、在平面直角坐标系 $x O y$ 中，直线l经过点 $M (1 ， 4)$ ，点F是坐标平面内一点，以F为圆心， $\sqrt{3}$ 为半径作 $⊙ F$ .若 $⊙ F$ 与直线l相离，点 $N (- 1 ， 0)$ 是 $⊙ F$ 关于直线l的“远点”，且 $⊙ F$ 关于直线l的“特征数”是 $6 \sqrt{6}$ ，直接写出直线l的函数解析式.

查看试题解析
25. 如图，在平面直角坐标系中，抛物线 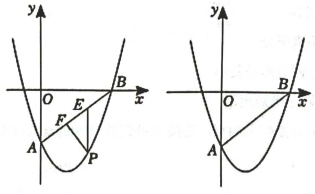$y = \frac{3}{4} x^{2} + b x + c$ 与直线 $A B$ 交于点 $A (0 ， - 3)$ ， $B (4 ， 0)$ .

(1)、求抛物线的函数解析式；

(2)、点P是直线 $A B$ 下方抛物线上一点，过点P作y轴的平行线，交 $A B$ 于点E，过点P作 $A B$ 的垂线，垂足为点F，求 $△ P E F$ 周长的最大值及此时点P的坐标；

(3)、在（2）中 $△ P E F$ 取得最大值的条件下，将该抛物线沿水平方向向左平移3个单位，点Q为点P的对应点，点N为原抛物线对称轴上一点.在平移后抛物线上确定一点M，使得以点B，Q，M，N为顶点的四边形是平行四边形，写出所有符合条件的点M的坐标，并写出求解点M的坐标的其中一种情况的过程.

查看试题解析