吉林省长春市南关区2023-2024学年九年级上学期12月月考数学试题

试卷更新日期：2024-02-22 类型：月考试卷

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. $\sqrt{{(- 4)}^{2}}$ 等于（）

A、4． B、-4． C、 $\pm 4$ ． D、2．

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{0.2}$ ． B、 $\sqrt{\frac{1}{2}}$ ． C、 $\sqrt{8}$ ． D、 $\sqrt{10}$ ．

查看试题解析
3. 已知关于x的一元二次方程 $(m - 2) x^{2} + 3 x + m^{2} - 4 = 0$ 有一个根是0，则m的值为（）

A、 $\pm 2$ ． B、-2． C、2． D、0．

查看试题解析
4. 若 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a + b}{b}$ 等于（）

A、 $\frac{5}{3}$ ． B、 $\frac{5}{2}$ ． C、 $\frac{3}{5}$ ． D、 $\frac{2}{5}$ ．

查看试题解析
5. 如图， $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F，若 $A B = 3$ ， $D E = 4$ ， $E F = 8$ ，则AC的长是（）

A、6． B、8． C、9． D、12．

查看试题解析
6. 如图，为测量池塘边A、B两点的距离，小宇同学在池塘的一侧选取一点O，测的OA、OB的中点分别是点D、E，且 $D E = 18$ 米，则A、B两点的距离是（）

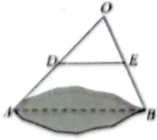A、9米． B、18米． C、36米． D、54米．

查看试题解析
7. 已知二次函数 $y = a {(x - h)}^{2} + k (a \neq 0)$ 函数值y与自变量x的部分对应值如下表：
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-22
-13
m
-1
2
3
2
-1
-6
…
其中m的值是（）

A、3． B、-1． C、2． D、-6．

查看试题解析
8. 已知函数 $y = {(x - m)}^{2} - 1$ （m为常数），当 $x > 1$ 时，函数值y随x的增大而增大，则m的取值范围是（）

A、 $m \leq 1$ ． B、 $m \geq 1$ ． C、 $m < 1$ ． D、 $m > 1$ ．

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

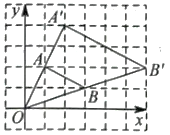
9. 若二次根式 $\sqrt{2 x - 5}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 不解方程，判断方程 $4 x^{2} = 3 x - 1$ 的根的情况是．

查看试题解析
11. 在比例尺为1：200000的长春市地图上，A中学和B中学的图上距离是5.75cm，则这两所学校的实际距离是km．

查看试题解析
12. 如图，在平面直角坐标系中有△OAB，以点O为位似中心将△OAB放大．若对应点A、 $A^{'}$ 的坐标分别为 $(1 ， 2)$ 、 $(2 ， 4)$ ，则△AOB与 $△ A^{'} O B^{'}$ 的面积之比为．

查看试题解析
13. 如图，在正方形ABCD中，对角线AC、BD交于点O，E为边BC的中点，AE、BD交于点F．若 $A B = 3 \sqrt{2}$ ，则OF的长为．

查看试题解析
14. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} - 2 a x + 2 (a < 0)$ 交x轴正半轴于点C，交y轴于点A， $A B ∥ x$ 轴交抛物线于点B，则△ABC的面积是．

查看试题解析

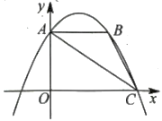
三、解答题（本大题共10小题，共78分）

15. 计算： $(\sqrt{50} - \sqrt{32} + \sqrt{\frac{3}{2}}) \times \sqrt{3}$ ．

查看试题解析
16. 求证：对于任意实数m，关于x的方程 $x^{2} - 2 m x + 2 m - 2 = 0$ 总有两个不相等的实数根．

查看试题解析
17. 通过配方，写出抛物线 $y = - 3 x^{2} + 6 x - 7$ 的开口方向、对称轴和顶点坐标．

查看试题解析
18. 如图，在灯塔A周围20海里水域有暗礁．一艘由西向东航行的轮船航行到O处发现，灯塔A在轮船的北偏东63°的方向上，且与轮船相距52海里．若该轮船不改变航向，通过计算说明该轮船是否有触暗礁的危险．【参考数据： $s i n 63 ° = 0.891$ ， $c o s 63 ° = 0.454$ ， $t a n 63 ° = 1.963$ 】

查看试题解析
19. 图①、图②、图③均是 $5 \times 5$ 的正方形网格，毎个小正方形的顶点称为格点，点A、B均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，不要求写画法，要求保留必要的作图痕迹．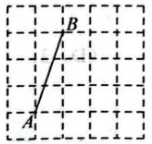
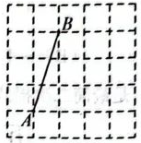
图① 图② 图③

(1)、在图①中以线段AB为边画△ABC，使点C在格点上，且 $t a n A = 1$ ．

(2)、在图②中以线段AB为边画△ABD，使 $t a n A = \frac{2}{3}$ ．

(3)、在图③中以线段AB为边画△ABE，使面积为3个平方单位．

查看试题解析
20. 如图，点E在矩形ABCD的BC边上，将 $△ A E B$ 沿AE翻折得到△AEF，过点F作 $P Q ∥ A B$ ，交BC、AD于点P、Q．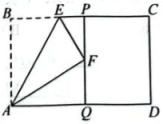

(1)、求证： $△ P E F ∽ △ Q F A$ ．

(2)、已知 $A B = \sqrt{3}$ ，若△AEF与△AFQ相似，直接写出BE的长．

查看试题解析
21. 为了提升居民生活质量，完善社区公共区域配套设施，今年夏天长春市在多个城区实施了旧城改造工程．已知某工程队在开始施工的7月份为某小区翻新道路 $12000 m^{2}$ ，为了在入冬前完成道路翻新工程，之后加快了工程进度，结果9月份为该小区翻新道路 $14520 m^{2}$ ．

(1)、求这两个月该工程队工作效率的月平均增长率．

(2)、若10月份该工程队的工作效率按此增长率增长，估计到10月末该工程队能否完成该小区共 $55000 m^{2}$ 的道路翻新任务？

查看试题解析
22. 两千多年前，古希腊数学家欧多克索斯发现：将一条线段AB分割成长、短两条线段AP、PB，若 $\frac{P B}{A P} = \frac{A P}{A B}$ ，则把这种分割叫做黄金分割，点P叫做线段AB的黄金分割点，这个比值叫做黄金比．

图① 图② 图③

(1)、如图①，点P是线段AB的黄金分割点，设 $A B = 1$ ， $A P = x$ ，求黄金比x的值．
（精确到0.001，参考数据： $\sqrt{2} = 1.4142$ ， $\sqrt{3} = 1.7321$ ， $\sqrt{5} = 2.2361$ ， $\sqrt{6} = 2.4495$ ）

(2)、如图②，在△ABC中， $A B = A C$ ， $∠ A = 36 °$ ， BD是△ABC的角平分线．
求证：点D是线段AC的黄金分割点．

(3)、如图③，点E是正方形ABCD的BC边的中点，以点E为圆心以ED长为半径画弧，交射线BC于点F，过点F作 $F G ⊥ B C$ 交射线AD于点G．若 $A G = 2 \sqrt{5}$ ，请直接写出AB的长．

查看试题解析
23. 法国数学家韦达在研究一元二次方程时发现：如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， $b^{2} - 4 a c \geq 0$ ）的两个实数根分别为 $x_{1}$ 、 $x_{2}$ ，那么 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ ．习惯上把这个结论称作“韦达定理”．

(1)、方程 $3 x^{2} - 4 x - 2 = 0$ 的两个实数根分别为 $x_{1}$ 、 $x_{2}$ ，求 $x_{1} + x_{2}$ 和 $x_{1} \cdot x_{2}$ 的值．

(2)、方程 $x^{2} + 2 x - 4 = 0$ 的两个实数根分别为 $x_{1}$ 、 $x_{2}$ ，求 $\frac{x_{1}}{x_{2}} + \frac{x_{2}}{x_{1}}$ 的值．

(3)、若 $x_{1}$ 、 $x_{2}$ 为关于x的方程 $x^{2} - (2 m - 3) x + m^{2} - \frac{3}{4} = 0$ 的两个实数根，求 $x_{1}^{2} + x_{2}^{2}$ 的最小值．

查看试题解析
24. 如图，在□ABCD中， $A B = 10$ ， $B C = 40$ ， $t a n B = \frac{4}{3}$ ．动点P从点B出发，先沿 $B - A$ 以每秒5个单位长度的速度运动，然后沿 $A - D - A$ 以每秒10个单位长度的速度继续运动．与此同时，动点Q从点B出发，沿BC方向以每秒5个单位长度的速度运动．当其中一点到达终点时，P、Q两点同时停止运动．设运动时间为t（秒），连结PQ．
（备用图）

(1)、当点P沿 $B - A - D$ 运动时，求AP的长（用含t的代数式表示）．

(2)、当 $P Q ⊥ B C$ 时，求t的值．

(3)、连结AQ，当△APQ的面积等于8个单位面积时，求t的值．

(4)、当点P在线段AD上时，把四边形PQBA沿PQ翻折得到四边形 $P Q B^{'} A^{'}$ ，直接写出 $B^{'} A^{'} ⊥ B C$ 时t的值．

查看试题解析

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	-22	-13	m	-1	2	3	2	-1	-6	…