云南省普洱市2023-2024学年七年级上学期期末数学试题

试卷更新日期：2024-02-22 类型：期末考试

进入出卷网下载

一、选择题：（共12小题，每小题3分，共36分）

1. 向东走5m，记为＋5m，那么走－10m，表示（）

A、向西走10m B、向东走10m C、向南走10m D、向北走10m

查看试题解析
2. 已知 $x$ 的相反数是 $- 5 ， y$ 的倒数是 $- \frac{1}{2} ， z$ 是多项式 $x^{3} + 5 x - 1$ 的次数，则 $\frac{x + y}{z}$ 的值为（）

A、3 B、 $\frac{7}{3}$ C、1 D、－1

查看试题解析
3. 若一个角的余角的 $3$ 倍比这个角的补角多12°，则这个角的度数为（）

A、 $38 °$ B、 $39 °$ C、 $40 °$ D、 $41 °$

查看试题解析
4. 下列计算正确的是（）

A、 $3 a^{2} + 2 a^{2} = 5 a^{4}$ B、 $- 2 (a + b) = - 2 a + 2 b$ C、 $6 x y - x = 6 y$ D、 $- a^{2} b + 2 a^{2} b = a^{2} b$

查看试题解析
5. A，B，C三点在同一直线上，线段AB＝5cm，BC＝4cm，那么A，C两点的距离是（）

A、1cm B、9cm C、1cm或9cm D、以上答案都不对

查看试题解析
6. 下列说法中错误的是（）

A、若 $a = b$ ，则 $3 - 2 a = 3 - 2 b$ B、若 $a = b$ ，则 $a c = b c$ C、若 $a c = b c$ ，则 $a = b$ D、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$

查看试题解析
7. 某正方体的每个面上都有一个汉字，如图是它的一种表面展开图，那么在原正方体中，与“时”字所在面相对的面上的汉字是（）

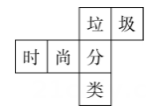A、分 B、垃 C、圾 D、类

查看试题解析
8. 按一定规律排列的单项式： $x^{2} ， 2 x^{4} ， 4 x^{6} ， 8 x^{8} ， 16 x^{10} ， 32 x^{12} ， ⋯$ ，第 $n$ 个单项式是 $()$

A、 $2^{n} x^{2 n}$ B、 $2^{n^{- 1}} x^{2 n}$ C、 $(2 n - 2) x^{2 n}$ D、 $n^{2} x^{2 n}$

查看试题解析
9. 如图，数轴上A、B、C三点所表示的数分别是a，6，c，已知 $A B = 8 ， a + c$ $= 0$ ，且 $c$ 是关于 $x$ 的方程 $(m - 4) x + 16 = 0$ 的一个解，则 $m$ 的值为 $()$

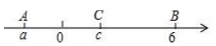A、－4 B、2 C、4 D、6

查看试题解析
10. 整理一批数据，由一人做需要40小时完成．现在计划先由一些人做2小时，再增加3人做4小时，完成这项工作的 $\frac{3}{4}$ ，则先安排（）人工作．

A、4 B、3 C、2 D、6

查看试题解析
11. 下列命题中，说法正确的有（）个
①非负数是指正数；②若 $| a | = | b |$ 则 $a = b$ ；③在时钟的钟面上下午2：40时的分针与时针夹角是 $16 0^{°}$ ④在数 $- \frac{π}{2} ， - 1.5 ， \frac{22}{7} ， - 1 ， 0$ 中无理数只有1个；⑤点 $A$ 与点 $B$ 之间的最短距离是线段 $A B$ ；⑥由四舍五入法得到的近似数 $8.6 \times 1 0^{3}$ 精确到百位；⑦ $- a$ 表示的数一定是负数；⑧数字879万用科学记数法表示为 $8.79 \times 1 0^{6}$ ．

A、6个 B、5个 C、4个 D、3个

查看试题解析
12. 已知关于 $x$ 的方程 $x - \frac{4 - a x}{6} = \frac{x + 4}{3} - 1$ 的解是正整数，则符合条件的所有整数 $a$ 的积是（）

A、-12 B、4 C、6 D、3

查看试题解析

二、填空题：（共4小题，每小题2分，共8分）

13. 若∠1=35°21′，则∠1的余角是．

查看试题解析
14. 若代数式 $x^{2} + 3 x$ 的值为 $5$ ，则代数式 $2 x^{2} + 6 x - 9$ 的值为．

查看试题解析
15. 如图，某海域有三个小岛 $A$ ， $B$ ， $O$ ，在小岛 $O$ 处观测到小岛 $A$ 在它北偏东 $60 °$ 的方向上，观测到小岛 $B$ 在它南偏东 $40 °$ 的方向上，则 $∠ A O B$ 的度数大小是.

查看试题解析
16. 规定：用 ${m}$ 表示大于 $m$ 的最小整数，例如 ${\frac{5}{3}} = 2 ， {4} = 5 ， {- 1.5} = - 1$ 等；用［m]表示不大于 $m$ 的最大整数，例如 $[\frac{7}{2}] = 3 ， [2] = 2 ， [- 3.2] = - 4$ ，

(1)、 ${2.4} =$ ； $[- 8] =$ ；

(2)、如果整数 $x$ 满足关系式： $3 {x} + 2 [x] = 18$ ，则 $x =$ ．

查看试题解析

三、解答题：（共8道题，共56分）

17. 计算： $- 2^{2} + 3 \times (- 1)^{2023} - 9 \div (- 3)$

查看试题解析
18. 解方程：

(1)、 $5 (x + 2) = 14 - 3 x$ ；

(2)、 $\frac{3 x - 2}{6} = 1 - \frac{x - 1}{3}$ ．

查看试题解析
19. 已知 $M = 2 x^{2} + a x - 5 y + b ， N = b x^{2} - \frac{3}{2} x - \frac{5}{2} y - 3$ ，其中a，b为常数．

(1)、求整式M－2N；

(2)、若整式M－2N的值与 $x$ 的取值无关，求 $(a + 2 M) - (2 b + 4 N)$ 的值．

查看试题解析
20. 如图，红军西征胜利纪念馆要在两块紧挨在一起的长方形荒地上修建一个半圆形花圃，尺寸如图所示（单位：米）

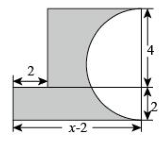(1)、求阴影部分的面积（用含x的代数式表示）；

(2)、当x＝8， $π$ 取3时，求阴影部分的面积．

查看试题解析

21. 某商场经销A，B两种商品，A种商品每件进价40元，售价60元；B种商品每件售价80元，利润率为60％．

(1)、每件A种商品利润率为， B种商品每件进价为；

(2)、若该商场同时购进A，B两种商品共50件，恰好总进价为2300元，则该商场购进A种商品多少件？

(3)、在“元旦”期间，该商场对A，B两种商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
不超过500元	不优惠
超过500元，但不超过800	按总售价打九折
超过800元	其中800元部分打八折优惠，超过800元的部分打七折优惠

按上述优惠条件，若小华一次性购买A，B商品实际付款675元，求小华此次购物打折前的总金额．

查看试题解析

22. 阅读材料：求 $1 + 2 + 2^{2} + 2^{3} + ⋯ ⋯ + 2^{2019} + 2^{2020}$ 的值．
解：设 $S = 1 + 2 + 2^{2} + 2^{3} + ⋯ ⋯ + 2^{2019} + 2^{2020}$ ①，将等式①的两边同乘以2，
得 $2 S = 2 + 2^{2} + 2^{3} + 2^{4} + ⋯ ⋯ + 2^{2020} + 2^{2021}$ ②，
用②－①得， $2 S - S = 2^{2021} - 1$ 即 $S = 2^{2021} - 1$ ．
即 $1 + 2 + 2^{2} + 2^{3} + ⋯ ⋯ + 2^{2019} + 2^{2020} = 2^{2021} - 1$ ．
请仿照此法计算：

(1)、请直接填写 $1 + 2 + 2^{2} + 2^{3}$ 的值为；

(2)、求 $1 + 5 + 5^{2} + 5^{3} + ⋯ ⋯ + 5^{10}$ 值；

(3)、请计算出 $1 - 10 + 1 0^{2} - 1 0^{3} + 1 0^{4} - 1 0^{5} + ⋯ ⋯ - 1 0^{2021} + 1 0^{2022} - 1 0^{2023}$ 的值．

查看试题解析
23. 如图1，已知线段AB＝44cm，CD＝4cm，线段CD在线段AB上运动（点C不与点A重合），点E、F分别是AC、BD的中点．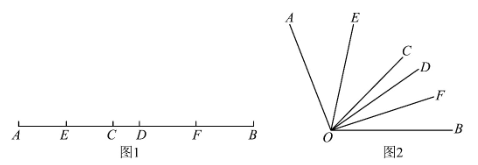

(1)、若AC＝10cm，则EF＝cm；

(2)、当线段CD在线段AB上运动时，试判断线段EF的长度是否会发生变化，如果不变，请求出线段EF的长度；如果变化，请说明理由；

(3)、我们发现角的很多规律和线段一样，如图2，已知∠COD在∠AOB内部转动，OE，OF分别平分∠AOC和∠BOD．类比以上发现的线段的规律，若∠EOF＝75°，∠COD＝35°则∠AOB＝．

查看试题解析
24. 已知数轴上两点A，B对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x_p ．

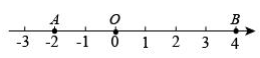(1)、若点p为线段AB的中点，则点p对应的数x_p＝；

(2)、点P在移动的过程中，其到点A、点B的距离之和为8，求此时点P对应的数x_p的值；

(3)、对于数轴上的三点，给出如下定义：若当其中一个点与其他两个点的距离恰好满足2倍关系时，则称该点是其他两个点的“2倍点”．如图，原点O是点A，B的2倍点．
现在，点A、点B分别以每秒4个单位长度和每秒1个单位长度的速度同时向右运动，同时点P以每秒3个单位长度的速度从表示数5的点向左运动．设出发t秒后，点P恰好是点A，B的“2倍点”，请写出此时的t值．

查看试题解析