四川省广元市苍溪县2023-2024学年九年级上学期数学期末考试试卷
试卷更新日期:2024-02-22 类型:期末考试
一、单选题
-
1. 下列运动项目图标中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 下列事件中,属于随机事件的是( )A、太阳从东边升起 B、打开电视,CCTV1正在播放《典籍里的中国》 C、过不在同一直线上的三个点确定一个圆 D、在一个装有白球和红球的袋子里摸出黑球4. 如图,A , B , C是上的三个点,若 , 则的度数为( )
2. 反比例函数的图象一定经过的点是( )A、 B、 C、 D、3. 下列事件中,属于随机事件的是( )A、太阳从东边升起 B、打开电视,CCTV1正在播放《典籍里的中国》 C、过不在同一直线上的三个点确定一个圆 D、在一个装有白球和红球的袋子里摸出黑球4. 如图,A , B , C是上的三个点,若 , 则的度数为( ) A、 B、 C、 D、5. 若是一元二次方程的一个根,则q的值为( )A、 B、2 C、 D、56. 如果小球在如图所示的图案上(去掉颜色的图案是中心对称图形也是轴对称图形)自由地滚动,并随机停留在某处,那么小球最终停留在灰色图案上的概率是( )
A、 B、 C、 D、5. 若是一元二次方程的一个根,则q的值为( )A、 B、2 C、 D、56. 如果小球在如图所示的图案上(去掉颜色的图案是中心对称图形也是轴对称图形)自由地滚动,并随机停留在某处,那么小球最终停留在灰色图案上的概率是( ) A、 B、 C、 D、7. 如图,将绕点A逆时针旋转得到 , 点、分别为点、的对应顶点,若 , 且于点 , 则的度数为( )
A、 B、 C、 D、7. 如图,将绕点A逆时针旋转得到 , 点、分别为点、的对应顶点,若 , 且于点 , 则的度数为( ) A、 B、 C、 D、8. “指尖上的非遗——麻柳刺绣”,针线勾勒之间,绣出世间百态.如图是在一幅长 , 宽的麻柳刺绣的四周镶嵌宽度相同的边框,制成的一幅矩形挂图,且整个挂图的面积是 . 设边框的宽度为 , 则列出的方程为( )
A、 B、 C、 D、8. “指尖上的非遗——麻柳刺绣”,针线勾勒之间,绣出世间百态.如图是在一幅长 , 宽的麻柳刺绣的四周镶嵌宽度相同的边框,制成的一幅矩形挂图,且整个挂图的面积是 . 设边框的宽度为 , 则列出的方程为( ) A、 B、 C、 D、9. 已知二次函数的图象如图所示,则一次函数的图象大致为( )
A、 B、 C、 D、9. 已知二次函数的图象如图所示,则一次函数的图象大致为( )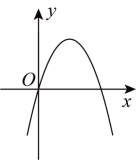 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,在中, , , , 的半径为1,点P是边上的动点,过点即P作的一条切线(点Q为切点),则切线长的最小值是( )
10. 如图,在中, , , , 的半径为1,点P是边上的动点,过点即P作的一条切线(点Q为切点),则切线长的最小值是( ) A、 B、3 C、 D、4
A、 B、3 C、 D、4二、填空题
-
11. 若函数是反比例函数,则的值等于 .12. 已知一元二次方程有两个相等的实数根,则m的值为 .13. 已知 , 两点都在抛物线上,那么 .14. 如图,点在反比例函数的图象上,轴于点 , 的面积为3,则的值为 .
 15. 如图,以点O为圆心,AB为直径的半圆过点C , 若C为的中点, , 则阴影部分的面积是 .
15. 如图,以点O为圆心,AB为直径的半圆过点C , 若C为的中点, , 则阴影部分的面积是 .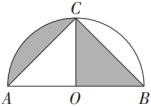 16. 如图,将绕点顺时针旋转,使点落在边上的点处,点落在点处,与相交于点 , 若 , , , 则的长为 .
16. 如图,将绕点顺时针旋转,使点落在边上的点处,点落在点处,与相交于点 , 若 , , , 则的长为 .
三、解答题
-
17. 解方程: .18. 已知反比例函数的图象位于第二、四象限.(1)、求k的取值范围;(2)、若点是该反比例函数图象上的两点,试比较函数值的大小.19. 赏红叶泡温泉玩转冰雪,这个冬天快来乐游广元.今年广元市某景点9月接待游客10万人,11月接待游客14.4万人.求该景点9月至11月接待游客的月平均增长率.20. 苍溪县“骑手驿站”建成使用,为严寒中的劳动者们带来丝丝暖意,让他们有更多的安全感、获得感、幸福感.刘军是苍溪县某区一名快递员,在他负责送货的区域附近有A , B , C , D四个“骑手驿站”,他主要在“骑手驿站”接热水、吃午饭.设他到这四个“骑手驿站”的可能性相等.(1)、他选择D“骑手驿站”接热水的概率是;(2)、请用列表或画树状图法表示他选择同一“骑手驿站”接热水、吃午饭的概率.21. 如图,的顶点都在边长为1的正方形组成的网格格点上, .
 (1)、将绕点O顺时针旋转得到 , 做出旋转后的;(2)、在旋转过程中,点B经过的路径为弧 , 求弧的长.22. 如图,一次函数的图象与反比例函数的图象交于第一象限C , D两点,与坐标轴交于A、B两点,连接(O是坐标原点).
(1)、将绕点O顺时针旋转得到 , 做出旋转后的;(2)、在旋转过程中,点B经过的路径为弧 , 求弧的长.22. 如图,一次函数的图象与反比例函数的图象交于第一象限C , D两点,与坐标轴交于A、B两点,连接(O是坐标原点). (1)、求反比例函数的表达式;(2)、求的面积;23. 如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B.
(1)、求反比例函数的表达式;(2)、求的面积;23. 如图,在⊙O中,PA是直径,PC是弦,PH平分∠APB且与⊙O交于点H,过H作HB⊥PC交PC的延长线于点B. (1)、求证:HB是⊙O的切线;(2)、若HB=4,BC=2,求⊙O的直径.24. 某商家出售的一种商品成本价为元/千克,市场调查发现,该商品每天的销售量y(千克)与售价x(元/千克)满足一次函数 . 设这种商品每天的销售利润为w元.(1)、求w关于x的函数解析式;(2)、该商品售价定为每千克多少元时,每天的销售利润最大?最大销售利润是多少?25. 把两个等腰直角三角形和按图①所示的位置摆放,将绕点C逆时针旋转()到图②所示位置,连接 , .
(1)、求证:HB是⊙O的切线;(2)、若HB=4,BC=2,求⊙O的直径.24. 某商家出售的一种商品成本价为元/千克,市场调查发现,该商品每天的销售量y(千克)与售价x(元/千克)满足一次函数 . 设这种商品每天的销售利润为w元.(1)、求w关于x的函数解析式;(2)、该商品售价定为每千克多少元时,每天的销售利润最大?最大销售利润是多少?25. 把两个等腰直角三角形和按图①所示的位置摆放,将绕点C逆时针旋转()到图②所示位置,连接 , . (1)、特例问题:如图①,与的数量关系是 , 与的位置关系是;(2)、探索解决:如图②,(1)中与的数量关系和位置关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、拓展应用:如图③,点D在内部,若 , , , 求线段的长.26. 如图,抛物线与x轴相交于两点,与y轴交于点C .
(1)、特例问题:如图①,与的数量关系是 , 与的位置关系是;(2)、探索解决:如图②,(1)中与的数量关系和位置关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、拓展应用:如图③,点D在内部,若 , , , 求线段的长.26. 如图,抛物线与x轴相交于两点,与y轴交于点C . (1)、求抛物线的解析式;(2)、抛物线的对称轴上是否存在一点M , 使的周长值最小?若存在,请求出点M的坐标;若不存在,请说明理由.(3)、在抛物线上有一点P , 过点P作x轴的垂线交x轴于点Q , 若是等腰直角三角形,求点P的坐标.
(1)、求抛物线的解析式;(2)、抛物线的对称轴上是否存在一点M , 使的周长值最小?若存在,请求出点M的坐标;若不存在,请说明理由.(3)、在抛物线上有一点P , 过点P作x轴的垂线交x轴于点Q , 若是等腰直角三角形,求点P的坐标.