【提高卷】2024年浙教版数学七年级下册2.3解二元一次方程组同步练习

试卷更新日期：2024-02-21 类型：同步测试

进入出卷网下载

一、选择题

1. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x + y = 2 k - 1 \\ x + 2 y = - 4 \end{array}$ 的解满足 $x + y > 1$ ，则 $k$ 的取值范围是（）

A、 $k < 1$ B、 $k < \frac{5}{2}$ C、 $k > \frac{5}{2}$ D、 $k > 4$

查看试题解析
2. 已知 ${\begin{array}{l} x = 4 \\ y = - 2 \end{array}$ 与 ${\begin{array}{l} x = - 2 \\ y = - 5 \end{array}$ 都是方程 $y = k x + b$ 的解，则 $k$ 与 $b$ 的值为（）

A、 $k = \frac{1}{2}$ ， $b = - 4$ B、 $k = - \frac{1}{2}$ ， $b = 4$ C、 $k = \frac{1}{2}$ ， $b = 4$ D、 $k = - \frac{1}{2}$ ， $b = - 4$

查看试题解析
3. 已知关于x，y的二元一次方程组 ${\begin{cases} a x - b y = - 2 \\ c x + d y = 4 \end{cases}$ 的解为 ${\begin{cases} x = 3 \\ y = 2 \end{cases}$ ，则方程组 ${\begin{cases} a x - b y + 2 a + b = - 2 \\ c x + d y - d = 4 - 2 c \end{cases}$ 的解为（）

A、 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = 3 \end{cases}$ C、 ${\begin{cases} x = 2 \\ y = 2 \end{cases}$ D、 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$

查看试题解析
4. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - 2 y = 2 k \\ 2 x + y = k + 1 \end{array}$ ，以下结论： $①$ 当 $k = 2$ 时，方程组的解也是方程 $3 x + y = 5$ 的解； $②$ 存在实数 $k$ ，使得 $x + y = 0$ ； $③$ 不论 $k$ 取什么实数， $3 x + 4 y$ 的值始终不变； $④$ 若 $2 x + 3 y = 3$ ，则 $k = 8 .$ 其中正确的是（）

A、①②③ B、①②④ C、①③④ D、①④

查看试题解析
5. 解方程组 ${\begin{array}{l} 2 x + 3 y = 8 ， \\ 3 x - 2 y = - 1 \end{array}$ 的思路可用如图的框图表示，圈中应填写的对方程①②所做的变形为（）

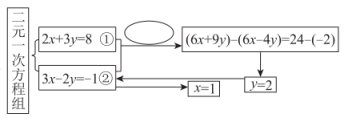A、①×2+②×3 B、①×2-②×3 C、①×3-②×2 D、①×3+②×2

查看试题解析
6. 用代入法解方程组 ${\begin{cases} x + 5 y = 6 ① \\ x - 3 y = 2 ② \end{cases}$
解：⑴由②得：x＝2＋3y；③

⑵把③代入①得：2＋3y＋5y＝6；

⑶解得：y＝1；

⑷把y＝1代入③，得x＝5，所以 ${\begin{cases} x = 5 \\ y = 1 \end{cases}$ .

在以上解题过程中，开始错的一步是（）

A、⑴ B、⑵ C、⑶ D、⑷

查看试题解析
7. 已知 $x_{1} ， x_{2} ， x_{3} ， ⋯ ， x_{55}$ 中每一个数值只能取2、0、 $- 1$ 中的一个，且满足 $x_{1} + x_{2} + ⋯ + x_{55} = - 19$ ， $x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + ⋯ + x_{55}^{2} = 55$ ，则 $x_{1} ， x_{2} ， x_{3} ， ⋯ ， x_{55}$ 中0的个数是（）

A、20 B、19 C、18 D、17

查看试题解析
8. 利用两块完全一样的长方体木块测量一张桌子的高度，首先按图①所示的方式放置，再交换两木块的位置，按图②所示的方式放置．测量的数据如图，则桌子的高度等于（）

A、 $60 c m$ B、 $65 c m$ C、 $70 c m$ D、 $75 c m$

查看试题解析

二、填空题

9. 若方程组 ${\begin{cases} 2 a - 3 b = m ， \\ 3 a + 5 b = n \end{cases}$ 的解是 ${\begin{cases} a = 3 \\ b = - 1 \end{cases}$ ，则方程组 ${\begin{cases} 2 (x - 1) - 3 (y + 2) = m ， \\ 3 (x - 1) + 5 (y + 2) = n \end{cases}$ 的解是.

查看试题解析
10. 当a=时，关于x、y的方程组 ${\begin{cases} 3 x - 5 y = 2 a ， \\ 2 x + 7 y = a - 18 \end{cases}$ 的解中．x、y互为相反数．

查看试题解析
11. 一架满载的波音客机，如果紧急着陆，从飞机接触跑道开始，飞机的速度v和时间t之间符合v=v₀+at(v₀ ， a为常数)，当t=0s时，v=60m/s，当t=4s时v=36m/s，则a= ．

查看试题解析
12. 已知关于x，y的方程组 ${\begin{cases} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{cases}$ ，则下列结论中正确的是
①当a=5时，方程组的解是 ${\begin{cases} x = 10 \\ y = 20 \end{cases}$
②当x，y值互为相反数时，a=20；
③当2^x·2^y=16时，a=18；
④不存在一个实数a，使得x=y．

查看试题解析

三、解答题

13. 解方程组：

(1)、 $\{\begin{matrix} 2 y - 3 x = 1 ， \\ x - y = - 1 . \end{matrix}$

(2)、 $\{\begin{matrix} 3 (x + y) - 4 (x - y) = 4 ， \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 . \end{matrix}$

查看试题解析
14. 小红和小风两人在解关于x，y的方程组 ${\begin{cases} a x + 3 y = 5 \\ b x + 2 y = 8 \end{cases}$ 时，小红只因看错了系数a，得到方程组的解为 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$ ，小风只因看错了系数b，得到方程组的解为 ${\begin{cases} x = 1 \\ y = 4 \end{cases}$ .

(1)、求a、b的值；

(2)、求原方程组的解．

查看试题解析
15. 王老师在上课时遇到下面问题：
已知 $x$ ， $y$ 满足方程组 ${\begin{array}{l} x + 3 y = - 1 \\ 3 x + y = 5 \end{array}$ ，求 $x + y$ 的值？
小明说：把方程组解出来，再求 $x + y$ 的值．
小刚说：把两个方程直接相加得 $4 x + 4 y = 4$ ，方程两边同时除以 $4$ ，解得 $x + y = 1$ ．
请你参考小明或小刚同学的做法，解决下面的问题：

(1)、已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x + y = 3 a + 1 ① \\ x + 2 y = 8 - 6 a ② \end{array}$ 的解满足 $x + y = - 5$ ，求 $a$ 的值；

(2)、已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 4 x - y = 4 m + 2 ① \\ x - 4 y = 8 + m ② \end{array}$ 的解满足 $x + y > 3$ ，求 $m$ 的取值范围．

查看试题解析

【提高卷】2024年浙教版数学七年级下册2.3解二元一次方程组 同步练习

一、选择题

二、填空题

三、解答题

【提高卷】2024年浙教版数学七年级下册2.3解二元一次方程组同步练习