【北师大版·数学】2024年中考二轮复习之锐角三角函数的综合题
试卷更新日期:2024-02-21 类型:二轮复习
一、选择题
-
1. 如图所示,有一天桥高为5米,是通向天桥的斜坡, , 市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使 , 则的长度约为(参考数据:)( )
 A、米 B、米 C、米 D、米2. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、3. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( )
A、米 B、米 C、米 D、米2. 小杰在一个高为的建筑物顶端,测得一根高出此建筑物的旗杆顶端的仰角为 , 旗杆与地面接触点的俯角为 , 那么该旗杆的高度是( )A、 B、 C、 D、3. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西方向的A处,若渔船沿北偏西方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东方向上,则B、C之间的距离为( ) A、15海里 B、30海里 C、海里 D、海里4. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
A、15海里 B、30海里 C、海里 D、海里4. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )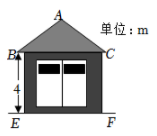 A、 B、 C、 D、5. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、86. 如图,矩形的对角线相交于点 . 若 , 则( )
A、 B、 C、 D、5. 在中, , , 若是锐角三角形,则满足条件的长可以是( )A、1 B、2 C、6 D、86. 如图,矩形的对角线相交于点 . 若 , 则( )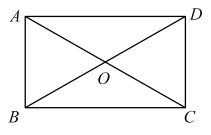 A、 B、 C、 D、7. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )
A、 B、 C、 D、7. 如图,某商场有一自动扶梯,其倾斜角为 , 高为7米.用计算器求的长,下列按键顺序正确的是( )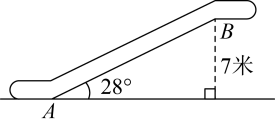 A、
A、 B、
B、 C、
C、 D、
D、 8. 已知“为锐角时,随着的增大而增大”,则的值更靠近( )A、 B、 C、 D、9. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )
8. 已知“为锐角时,随着的增大而增大”,则的值更靠近( )A、 B、 C、 D、9. 如图,在网格中小正方形的边长均为1,△ABC的顶点都在格点上,则等于( )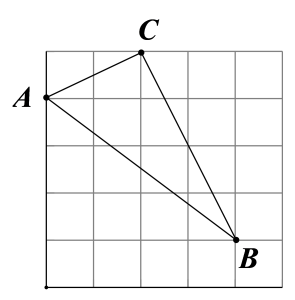 A、 B、 C、 D、10. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )
A、 B、 C、 D、10. 如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=;④△AMN∽△CAB.正确的有( )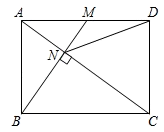 A、①②③④ B、①②③ C、①②④ D、②③④
A、①②③④ B、①②③ C、①②④ D、②③④二、填空题
-
11. 菱形的边长为2, , 点、分别是、上的动点,的最小值为.
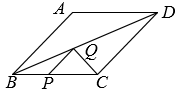 12. 若 , 且 , 则度.13. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.
12. 若 , 且 , 则度.13. 如图,在△ABC中,BC= ,∠C=45°,AB= AC,则AC的长为.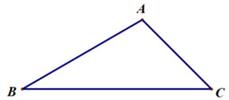 14. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 .
14. 某数学活动小组要测量一建筑物的高度,如图,他们在建筑物前的平地上选择一点 , 在点和建筑物之间选择一点 , 测得 . 用高的测角仪在处测得建筑物顶部的仰角为 , 在处测得仰角为 , 则该建筑物的高是 . 15. 2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在处用仪器测得赛场一宣传气球顶部处的仰角为 , 仪器与气球的水平距离为20米,且距地面高度为1.5米,则气球顶部离地面的高度是米(结果精确到0.1米,).
15. 2023年岳阳举办以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在处用仪器测得赛场一宣传气球顶部处的仰角为 , 仪器与气球的水平距离为20米,且距地面高度为1.5米,则气球顶部离地面的高度是米(结果精确到0.1米,).
三、计算题
-
16. 先化简,再求值: , 其中 .
四、解答题
-
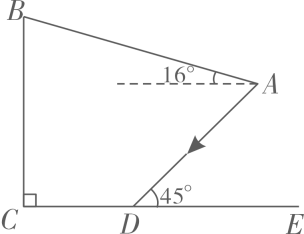
17. 为建设美好公园社区,增强民众生活幸福感,某社区服务中心在文化活动室墙外安装遮阳篷,便于社区居民休憩.
如图,在侧面示意图中,遮阳篷AB长为5米,与水平面的夹角为16°,且靠墙端离地高BC为4米,当太阳光线AD与地面CE的夹角为45°时,求阴影CD的长.(结果精确到0.1米;参考数据: , , )

五、作图题
-
18. 如图,在中, .
 (1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.
(1)、实践与操作:用尺规作图法过点作边上的高;(保留作图痕迹,不要求写作法)(2)、应用与计算:在(1)的条件下, , , 求的长.六、综合题
-
19. 如图,是菱形的对角线.(1)、尺规作图:将绕点逆时针旋转得到 , 点旋转后的对应点为保留作图痕迹,不写作法;(2)、在(1)所作的图中,连接 , .
求证:∽;
若 , 求的值.
七、实践探究题
-
20. 【问题背景】由光的反射定律知:反射角等于入射角(如图,即).小军测量某建筑物高度的方法如下:在地面点E处平放一面镜子,经调整自己位置后,在点D处恰好通过镜子看到建筑物AB的顶端A . 经测得,小军的眼睛离地面的距离 , , , 求建筑物AB的高度.

【活动探究】
观察小军的操作后,小明提出了一个测量广告牌高度的做法(如图):他让小军站在点D处不动,将镜子移动至处,小军恰好通过镜子看到广告牌顶端G , 测出;再将镜子移动至处,恰好通过镜子看到广告牌的底端A , 测出 . 经测得,小军的眼睛离地面距离 , , 求这个广告牌AG的高度.

【应用拓展】
小军和小明讨论后,发现用此方法也可测量出斜坡上信号塔AB的高度.他们给出了如下测量步骤(如图):①让小军站在斜坡的底端D处不动(小军眼睛离地面距离),小明通过移动镜子(镜子平放在坡面上)位置至E处,让小军恰好能看到塔顶B;②测出;③测出坡长;④测出坡比为(即).通过他们给出的方案,请你算出信号塔AB的高度(结果保留整数).

-
-
-
-