【北师大版·数学】2024年中考二轮复习之抛物线的综合题
试卷更新日期:2024-02-21 类型:二轮复习
一、选择题
-
1. 如图,二次函数图象的一部分与x轴的一个交点坐标为 , 对称轴为直线 , 结合图象给出下列结论:
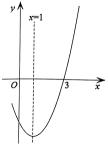
①;②;③;
④关于x的一元二次方程有两个不相等的实数根;
⑤若点 , 均在该二次函数图象上,则.其中正确结论的个数是( )
A、4 B、3 C、2 D、12. 已知m>0,关于x的一元二次方程(x+1)(x﹣2)﹣m=0的解为x1 , x2(x1<x2),则下列结论正确的是( )A、x1<﹣1<2<x2 B、﹣1<x1<2<x2 C、﹣1<x1<x2<2 D、x1<﹣1<x2<23. 方程x2+3x﹣1=0的根可视为函数y=x+3的图象与函数y= 的图象交点的横坐标,那么用此方法可推断出方程x3+x﹣1=0的实根x0所在的范围是( )A、 B、 C、 D、4. 如图1,矩形 中, ,点 分别是 上两动点,将 沿着对折得,将沿着 对折得 ,将 沿着 对折,使 三点在一直线上,设 的长度为x, 的长度为y,在点p的移动过程中,y与x的函数图象如图2,则函数图象最低点的纵坐标为( ) A、 B、 C、 D、5. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( )
A、 B、 C、 D、5. 如图, 为矩形 的对角线,已知 , .点P沿折线 以每秒1个单位长度的速度运动(运动到D点停止),过点P作 于点E,则 的面积y与点P运动的路程x间的函数图象大致是( ) A、
A、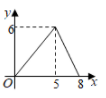 B、
B、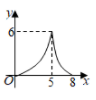 C、
C、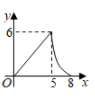 D、
D、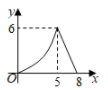 6. 某超市一种干果现在的售价是每袋元,每星期可卖出袋,经市场调研发现,如果在一定范围内调整价格,每涨价元,每星期就少卖出袋,已知这种干果的进价为每袋元,设每袋涨价元 , 每星期的销售量为袋 , 每星期销售这种干果的利润为元则与 , 与满足的函数关系分别是( )A、一次函数,二次函数 B、一次函数,反比例函数
6. 某超市一种干果现在的售价是每袋元,每星期可卖出袋,经市场调研发现,如果在一定范围内调整价格,每涨价元,每星期就少卖出袋,已知这种干果的进价为每袋元,设每袋涨价元 , 每星期的销售量为袋 , 每星期销售这种干果的利润为元则与 , 与满足的函数关系分别是( )A、一次函数,二次函数 B、一次函数,反比例函数
C、反比例函数,二次函数 D、反比例函数,一次函数7. 已知二次函数的图象经过点 , , 在范围内有最大值为 , 最小值为 , 则的取值范围是( )A、 B、 C、 D、8. 如图.抛物线与x轴交于点和点 , 与y轴交于点C.下列说法:①;②抛物线的对称轴为直线;③当时,;④当时,y随x的增大而增大;⑤(m为任意实数)其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个9. 如图,在中, , 点是边上一动点不与
A、1个 B、2个 C、3个 D、4个9. 如图,在中, , 点是边上一动点不与
点 , 重合 , 过点作交于点设 , 的长为 ,
的面积为 , 则与 , 与满足的函数关系分别为( ) A、一次函数关系,二次函数关系
A、一次函数关系,二次函数关系
B、反比例函数关系,二次函数关系
C、一次函数关系,反比例函数关系
D、反比例函数关系,一次函数关系10. 设二次函数是实数 , 则( )A、当时,函数的最小值为 B、当时,函数的最小值为 C、当时,函数的最小值为 D、当时,函数的最小值为二、填空题
-
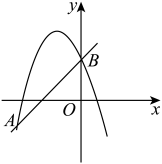
11. 将抛物线向下平移1个单位长度,再向右平移个单位长度后,得到的新抛物线经过原点.12. 如图,已知抛物线与直线交于、两点,则关于的不等式的解集是.
 13. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .
13. 如图1,在中, , 动点从点出发,以每秒1个单位的速度沿线段运动到点停止,同时动点从点出发,以每秒4个单位的速度沿折线运动到点停止.图2是点运动时,的面积与运动时间函数关系的图象,则的值是 .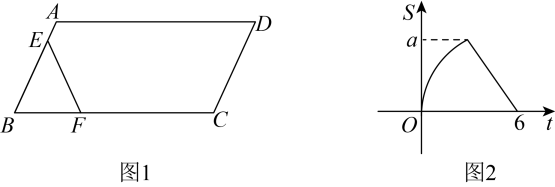 14. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .
14. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .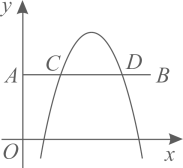 15. 华罗庚说过:“复杂的问题要善于‘退’,足够地‘退’,‘退’到最原始而不失重要性的地方,是学好数学的一个诀窍.”可见,复杂的问题有时要“退”到本质上去研究.如图,已知抛物线的图象与f的图象关于直线对称,我们把探索线的变化规律“退”到探索点的变化规律上去研究,可以得到图象f所对应的关于x与y的关系式为 . 若抛物线与g的图象关于对称,则图象g所对应的关于x与y的关系式为 .
15. 华罗庚说过:“复杂的问题要善于‘退’,足够地‘退’,‘退’到最原始而不失重要性的地方,是学好数学的一个诀窍.”可见,复杂的问题有时要“退”到本质上去研究.如图,已知抛物线的图象与f的图象关于直线对称,我们把探索线的变化规律“退”到探索点的变化规律上去研究,可以得到图象f所对应的关于x与y的关系式为 . 若抛物线与g的图象关于对称,则图象g所对应的关于x与y的关系式为 .
三、解答题
-
16. 某服装店经销A,B两种T恤衫,进价和售价如下表所示:
进价(元/件)
45
60
售价(元/件)
66
90
(1)、第一次进货时,服装店用6000元购进A,B两种T恤衫共120件,全部售完获利多少元?(2)、受市场因素影响,第二次进货时,A种T恤衫进价每件上涨了5元,B种T恤衫进价每件上涨了10元,但两种T恤衫的售价不变.服装店计划购进A,B两种T恤衫共150件,且B种T恤衫的购进量不超过A种T恤衫购进量的2倍.设此次购进A种T恤衫m件,两种T恤衫全部售完可获利W元.①请求出W与m的函数关系式;
②服装店第二次获利能否超过第一次获利?请说明理由.
17. 已知抛物线交轴于 , 两点,其中点的坐标为 , 对称轴为点 , 为坐标平面内两点,其坐标为 , .(1)、求抛物线的解析式及顶点坐标;(2)、连接 , 若抛物线向下平移个单位时,与线段只有一个公共点,求的取值范围.18. 在平面直角坐标系中,点 , 都在抛物线上,且 , .
(1)、当时,比较 , 的大小关系,并说明理由;
(2)、若存在 , , 满足 , 求的取值范围.四、综合题
-
19. 如图,直线y=-x+m与抛物线y=ax2+bx都经过点A(6,0),点B,过B作BH垂直x轴于H,OA=3OH.直线OC与抛物线AB段交于点C.
 (1)、求抛物线的解析式;(2)、当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)、在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.
(1)、求抛物线的解析式;(2)、当点C的纵坐标是时,求直线OC与直线AB的交点D的坐标;(3)、在(2)的条件下将△OBH沿BA方向平移到△MPN,顶点P始终在线段AB上,求△MPN与△OAC公共部分面积的最大值.五、实践探究题
-
20. 根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
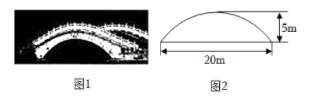
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
素材2
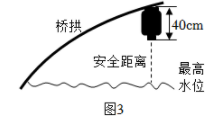
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
-