(华师大版)2023-2024学年度第二学期七年级数学10.1 轴对称 同步测试
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
1. 下列标志中,可以看作是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )A、
2. 将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 ( )
3. 如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为 ( ) A、30° B、50° C、90° D、100°4. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形5. 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
A、30° B、50° C、90° D、100°4. 已知,△ABC和△ADC关于直线AC轴对称,如果∠BAD+∠BCD=160°,那么△ABC是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形5. 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )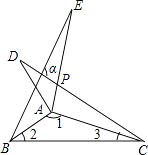 A、90° B、108° C、110° D、126°6. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、
A、90° B、108° C、110° D、126°6. 下面是四位同学所作的 关于直线 对称的图形,其中正确的是( )A、 B、
B、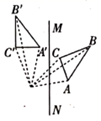 C、
C、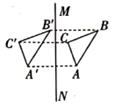 D、
D、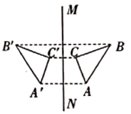 7. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( )
7. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( ) A、1个 B、2个 C、3个 D、4个8. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD 沿EF 折叠,A,D两点分别与点A',D'对应.若∠CFE=2∠CFD',设∠CFD'=x°,∠CFE=y°,则根据题意,可列方程组为 ( )
A、1个 B、2个 C、3个 D、4个8. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD 沿EF 折叠,A,D两点分别与点A',D'对应.若∠CFE=2∠CFD',设∠CFD'=x°,∠CFE=y°,则根据题意,可列方程组为 ( )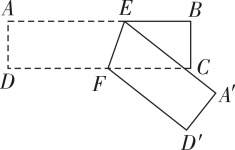 A、 B、 C、 D、9. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )
A、 B、 C、 D、9. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )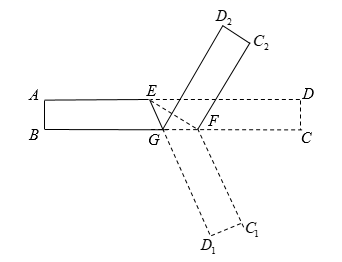 A、 B、 C、 D、10. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D',C'的位置.如果∠EFB=65°,那么∠AED'等于( )
A、 B、 C、 D、10. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D',C'的位置.如果∠EFB=65°,那么∠AED'等于( )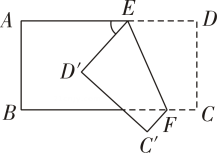 A、70° B、65° C、50° D、25°
A、70° B、65° C、50° D、25°二、填空题
-
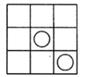
11. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。
 12. 已知中是钝角,以所在直线为对称轴作 , 若 , 则的度数为 .13. 如图,将一张长方形纸片按如图所示折叠,如果 , 那么 .
12. 已知中是钝角,以所在直线为对称轴作 , 若 , 则的度数为 .13. 如图,将一张长方形纸片按如图所示折叠,如果 , 那么 . 14. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个.
14. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成轴对称且也以格点为顶点的三角形,这样的三角形共有个. 15. 如图,把一张长方形纸片ABCD沿AF折叠,已知∠DBC=20°,当∠BAF=度时,才能使AB'∥BD.
15. 如图,把一张长方形纸片ABCD沿AF折叠,已知∠DBC=20°,当∠BAF=度时,才能使AB'∥BD.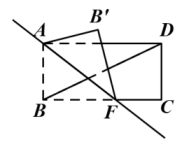
三、解答题
-
16. 如图,△ABC和△ADE关于直线l对称,已知AB=15,DE=10,∠D=70°.求∠B的度数及BC、AD的长度
 17. 如图,点P是∠AOB内一点,分别作出P点关于OA、OB的对称点E、F,连接EF交OA于M,交OB于N,EF=15,求△PMN的周长.
17. 如图,点P是∠AOB内一点,分别作出P点关于OA、OB的对称点E、F,连接EF交OA于M,交OB于N,EF=15,求△PMN的周长.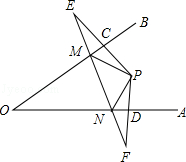 18. 如图,△ABC与△A′B′C′关于直线l对称,若∠A=76°,∠C′=48°.求∠B的度数.
18. 如图,△ABC与△A′B′C′关于直线l对称,若∠A=76°,∠C′=48°.求∠B的度数. 19. 如图,在每个小正方形的边长为1的网格中,点A、B、C、D均在格点上,点P是直线CD上的点连BP,点A′是点A关于直线BP的对称点
19. 如图,在每个小正方形的边长为1的网格中,点A、B、C、D均在格点上,点P是直线CD上的点连BP,点A′是点A关于直线BP的对称点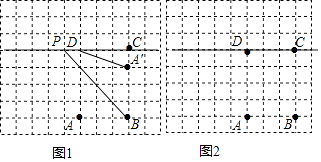
(Ⅰ)在图①中,当DP=1(点P在点D的左侧)时,计算DA′的值;
(Ⅱ)当DA′取值最小值时,请在如图②所示的网格中,用无刻度的直尺画出点A′,并简要说明点A′的位置如何找到的(不要求证明)
20. 如图,是一张三角形的纸片,点、分别是边、上的点将沿折叠,点落在点的位置.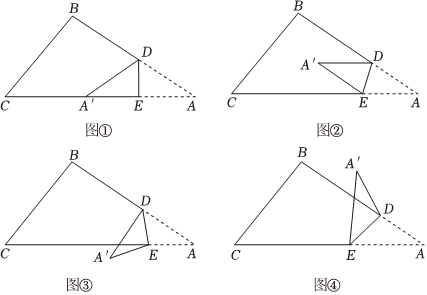 (1)、如图 , 当点落在边上时,若 , 求的大小.(2)、如图 , 当点落在内部时,若 , , 求的大小.(3)、当点落在外部时,
(1)、如图 , 当点落在边上时,若 , 求的大小.(2)、如图 , 当点落在内部时,若 , , 求的大小.(3)、当点落在外部时,如图 , 若 , , 则
如图 , 、和的数量关系为 .