(华师大版)2023-2024学年度第二学期七年级数学9.1 三角形 同步测试
试卷更新日期:2024-02-21 类型:同步测试
一、选择题
-
1. 下列各图中,正确画出AC边上的高的是( )A、
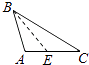 B、
B、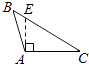 C、
C、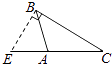 D、
D、 2. 如图所示的网格由边长相同的小正方形组成,点 , , , , , , 均在小正方形的顶点上,则的重心是( )
2. 如图所示的网格由边长相同的小正方形组成,点 , , , , , , 均在小正方形的顶点上,则的重心是( )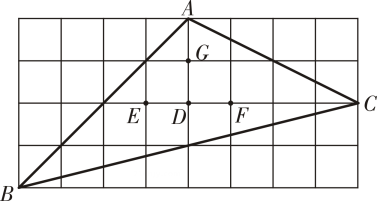 A、点 B、点 C、点 D、点3. 在△ABC中,画出边AC上的高,画法正确的是( )
A、点 B、点 C、点 D、点3. 在△ABC中,画出边AC上的高,画法正确的是( )
A、 B、
B、 C、
C、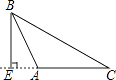 D、
D、 4. 如图,已知直线AB∥CD,一条直线分别截直线AB,CD于点E,F,∠AEF的平分线交CD于点M,G是射线MD上的动点(不与点M,F重合),∠FEG的平分线交CD于点H.设∠MEH=α,∠EGF=β,现有下列四个判断:①2α=β,②2α-β=180°.③α-β=30°.④2α+β=180°.其中可能正确的是( )
4. 如图,已知直线AB∥CD,一条直线分别截直线AB,CD于点E,F,∠AEF的平分线交CD于点M,G是射线MD上的动点(不与点M,F重合),∠FEG的平分线交CD于点H.设∠MEH=α,∠EGF=β,现有下列四个判断:①2α=β,②2α-β=180°.③α-β=30°.④2α+β=180°.其中可能正确的是( ) A、①② B、①④ C、①③④ D、②③④5. 将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )
A、①② B、①④ C、①③④ D、②③④5. 将一个三角尺按如图所示的方式放置,∠ACB=90°,∠ABC=60°,点B,C分别在直线PQ,MN 上.若 PQ∥MN,∠ACM=44°,则∠PBC的度数为( )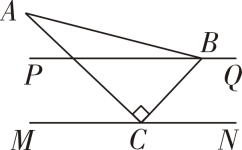 A、46° B、44° C、22° D、20°6. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )
A、46° B、44° C、22° D、20°6. 将一副三角板按如图所示方式摆放,使有刻度的边互相垂直,则( )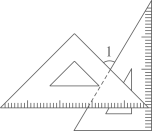 A、 B、 C、 D、7. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm8. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种9. 已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A、 B、 C、 D、7. 现有两根木棒,它们的长分别是20cm和30cm.若要钉一个三角架,则下列四根木棒的长度应选( )A、10cm B、30cm C、50cm D、70cm8. 四根木棒的长度分别为 , , , , 现从中取三根,使它们首尾顺次相接组成一个三角形,则这样的取法共有( )A、1种 B、2种 C、3种 D、4种9. 已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A、6个; B、5个; C、4个; D、3个.10. 一个三角形的两边长分别是3和7,且第三边长为整数,这样的三角形周长最大的值为( )A、15 B、16 C、18 D、19二、填空题
-
11. 如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD=
 12. 如图,一条公路修到湖边时,需要弯折绕湖而过.若第一次弯折的角∠A=110°,第二次弯折的角∠B=145°,则第三次弯折的角∠C=°时,道路CE 恰好与AD 平行.
12. 如图,一条公路修到湖边时,需要弯折绕湖而过.若第一次弯折的角∠A=110°,第二次弯折的角∠B=145°,则第三次弯折的角∠C=°时,道路CE 恰好与AD 平行. 13. 将一副三角尺按如图所示放置,给出下列结论:
13. 将一副三角尺按如图所示放置,给出下列结论:
①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④若∠2=30°,则∠4=∠C一定成立.其中正确的有(填序号)
14. 若一个三角形两边长分别为2、5,则此三角形的周长c的取值范围为 .15. 若一个三角形的三边长分别是 , , , 则x的取值范围是 .三、解答题
-
16. 如图,在△ABC中(AB>BC),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
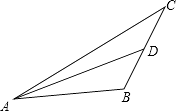 17. 若a,b,c是 的三边的长,化简|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|.18. 如图,已知 是 的一条中线,延长 至 ,使得 ,连接 . 如果 ,试求 的取值范围.
17. 若a,b,c是 的三边的长,化简|a﹣b﹣c|+|b﹣c﹣a|+|c+a﹣b|.18. 如图,已知 是 的一条中线,延长 至 ,使得 ,连接 . 如果 ,试求 的取值范围. 19. 如图,已知DB∥AC,AB∥EC,且点D,A,E在同一条直线上,设∠BAC=x,∠D+∠E=y.
19. 如图,已知DB∥AC,AB∥EC,且点D,A,E在同一条直线上,设∠BAC=x,∠D+∠E=y. (1)、试用含x的代数式表示y.(2)、当x=90°,且∠D=2∠E时,求∠D与∠E的度数.并说明DB与CE具有怎样的位置关系?20. 我们将内角互为对顶角的两个三角形称为“对顶二角形”.例如,在图1中,的内角与的内角为对顶角,则与为“对顶三角形”,根据三角形三个内角和是 , “对顶三角形”有如下性质: .
(1)、试用含x的代数式表示y.(2)、当x=90°,且∠D=2∠E时,求∠D与∠E的度数.并说明DB与CE具有怎样的位置关系?20. 我们将内角互为对顶角的两个三角形称为“对顶二角形”.例如,在图1中,的内角与的内角为对顶角,则与为“对顶三角形”,根据三角形三个内角和是 , “对顶三角形”有如下性质: . (1)、性质理解:
(1)、性质理解:如图1,在“对顶三角形”与中,则 , 则 .
(2)、性质应用:如图2,在中,分别平分和 , 若 , 比大8°,求的度数.
(3)、拓展提高:如图3,是的角平分线,且和的平分线和相交于点P,设 , 请尝试求出的度数(用含的式了表示).