浙江省绍兴市2023-2024学年第一学期七年级期末数学模拟试卷

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题（本大题有10小题，每小题3分，共30分）

1. 2023的相反数等于（）

A、2023 B、 $- 2023$ C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2.
神舟十五号载人飞船于2022年11月29日成功发射，载人飞船与空间站组合体对接后．在距离地球表面约430000米左右的轨道上运行． 430000米用科学记数法表示是（）

A、 $4.3 \times 1 0^{3}$ 米 B、 $4.3 \times 1 0^{5}$ 米 C、 $43 \times 1 0^{4}$ 米 D、 $0.43 \times 1 0^{6}$ 米

查看试题解析
3. 已知一个边长为米的正方形，面积是 $37$ 平方米，则a的取值范围是（）

A、 $4 < a < 5$ B、 $5 < a < 6$ C、 $6 < a < 7$ D、 $7 < a < 8$

查看试题解析
4. 若 $x = 1$ 是关于的方程 $2 x + 3 a = 5$ 的解，则的值为（）

A、2 B、3 C、1 D、 $\frac{1}{3}$

查看试题解析
5. 下列方程的变形中，不正确的是（）

A、由 $7 x = 6 x - 1$ ，得 $7 x - 6 x = 1$ B、由 $- \frac{1}{3} x = 9$ ，得 $x = - 27$ C、由 $5 x = 10$ ，得 $x = 2$ D、由 $3 x = 6 - x$ ，得 $3 x + x = 6$

查看试题解析
6. 如图，点C为线段 $A B$ 的中点，点D在线段 $C B$ 上，如果 $A B = 10$ ， $D B = 2$ ，那么线段 $C D$ 的长是（）

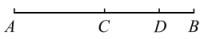A、2 B、3 C、4 D、5

查看试题解析
7. 有理数m、n在数轴上的位置如图所示，
则下列关于 $- m$ ， $- n$ ， $m$ ，的大小关系正确的是（）

A、 $m > n > 0$ B、 $m > - m > n$ C、 $m > - n > 0$ D、 $- n > n > - m$

查看试题解析
8. 如图，利用工具测量角，有如下4个结论：
① $∠ A O C = 90 °$ ；
② $∠ A O B = ∠ B O C$ ；
③ $∠ A O B$ 与 $∠ B O C$ 互为余角；
④ $∠ A O B$ 与 $∠ A O D$ 互为补角．
上述结论中，所有正确结论的序号是（）

A、①②③ B、①② C、③④ D、①③④

查看试题解析
9. 某个体商贩在一次买卖中，同时卖出两件上衣，售价都是135元，若按成本计，其中一件盈利25%，另一件亏本25%，在这次买卖中他（）．

A、不赚不赔 B、赚9元 C、赔18元 D、赚18元

查看试题解析
10. 如图，下列各图都是由小正方形搭建而成，按照各图的搭建规律继续添加小正方形，
则第2023个图形中共有小正方形的数量可能是（）

A、3034 B、3035 C、6064 D、6065

查看试题解析

二、填空题（本大题有6小题，每小题3分，共18分．）

11. $- 8$ 的立方根是．

查看试题解析
12. nbsp；.已知单项式 $2 x^{n + 2} y^{4} 与 5 x^{5} y^{2 + m}$ 是同类项，则 $n^{m}$ =.

查看试题解析
13. 按如图所示的程序计算，若输入的 $a = 3$ ， $b = 4$ ，则输出的结果为．

查看试题解析
14. 如图，点C、D在线段AB上，点C为AB中点，若AC=5cm，BD=2cm，则CD=cm．

查看试题解析
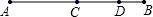15. 如图，将一个三角板 $60 °$ 角的顶点与另一个三角板的直角顶点重合， $∠ 1 = 25 ° 2 0^{'}$ ，则 $∠ 2 =$ ．

查看试题解析
16. 如图①，点C在线段AB上，图中有三条线段AB、AC和BC ，在这三条线段中，若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段AB的“巧点”，如图②，点A和B在数轴上表示的数分别是﹣10和26，点C是线段AB的巧点，则点C在数轴上表示的数为．

查看试题解析

三、解答题（本大题有8小题，共52分．解答需写出必要的文字说明、演算步骤或证明过程．）

17. 计算：

(1)、 $- 12 \times (\frac{1}{6} + \frac{1}{3} - \frac{1}{4})$

(2)、 $- 1^{2} - \frac{1}{4} \times [(- 3)^{2} - 5]$

查看试题解析
18. 解方程

(1)、2（x﹣1）²=8；

(2)、（x﹣2）³=﹣1．

查看试题解析
19. 先化简，再求值： $- (2 a^{2} - 6 a b + 9) + 2 (4 a b + a^{2} - 4.5)$ ，其中 $a = - \frac{2}{3}$ ， $b = 6$ ．

查看试题解析
20. 解方程：

(1)、 $2 - 3 (x - 1) = 2 (x - 2)$ ；

(2)、 $\frac{3 x + 2}{5} = 1 + \frac{2 x - 1}{3}$ ．

查看试题解析
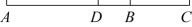21. 如图，已知线段 $A B = a$ ，延长 $A B$ 至点 $C$ ，使 $B C = \frac{1}{2} A B$ ． $D$ 为线段 $A C$ 的中点．

(1)、求线段 $A C$ 的长（用含的代数式表示）．

(2)、若 $B D = 3 c m$ ，求a的值．

查看试题解析
22. 目前，某城市“一户一表”居民用电实行阶梯电价，具体收费标准如下．
一户居民一个月用电量（单位：度）
电价（单位：元/度）
第1档
不超过180度的部分
0.5
第2档
超过180度的部分
0.7

(1)、若该市某户12月用电量为200度，该户应交电费元；

(2)、若该市某户12月用电量为x度，请用含x的代数式分别表示 $0 \leq x \leq 180$ 和 $x > 180$ 时该户12月应交电费多少元；

(3)、若该市某户12月应交电费125元，则该户12月用电量为多少度？

查看试题解析
23. 如图，以直线 $A B$ 上一点 $O$ 为端点作射线 $O C$ ，使 $∠ B O C = 70 °$ ，将一个直角三角形的直角顶点放在点O处．（注： $∠ D O E = 90 °)$ ）

(1)、如图①，若直角三角板 $D O E$ 的一边 $O D$ 放在射线 $O B$ 上，则 $∠ C O E =$ ；

(2)、如图②，将直角三角板 $D O E$ 绕点O逆时针方向转动到某个位置，若 $O C$ 恰好平分 $∠ B O E$ ，求 $∠ C O D$ 的度数；

(3)、如图③，将直角三角板 $D O E$ 绕点O转动，如果 $O D$ 始终在 $∠ B O C$ 的内部，试猜想 $∠ B O D$ 和 $∠ C O E$ 有怎样的数量关系？并说明理由．

查看试题解析
24. 【概念学习】
点A，B，C为数轴上的三点，如果点C到A的距离是点C到B的距离的2倍，那么我们就称点C是{A、B}的偶点．
如图1，点A表示的数为-2，点B表示的数为1，表示0的点C到点A的距离是2，到点B的距离是1，那么点C是{A、B}的偶点；表示-1的点D到点A的距离是1，到点B的距离是2，那么点D就不是{A、B}的偶点，但点D是{B、A}的偶点．

【初步探究】
已知如图2，M，N为数轴上两点，点M表示的数为-1，点N表示的数为5，若点F是{M、N}的偶点，回答下列问题：

(1)、当F在点M ， N之间，点F表示的数为；

(2)、当F为数轴上一点，点F表示的数为；

(3)、【深入思考】如图2，P、Q为数轴上两点，点P表示的数为 $- 20$ ，点Q表示的数为40，现有一个动点E从点Q出发，以每秒2个单位的速度向左运动，到达点P停止，若运动时间为t ，求当t为何值时，P ， Q ， E中恰有一个点为其余两点的偶点？

查看试题解析

一户居民一个月用电量（单位：度）		电价（单位：元/度）
第1档	不超过180度的部分	0.5
第2档	超过180度的部分	0.7