浙江省杭州市保俶塔教育集团2023学年第一学期期中质量检测九年级 数学
试卷更新日期:2024-02-21 类型:期中考试
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 已知⊙O的半径为5,点P在⊙O外,则OP的长可能是( )A、3 B、4 C、5 D、62. 把图形绕O点顺时针旋转180度后,得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 二次函数y=(x﹣1)2﹣3的最小值是( )A、2 B、1 C、﹣2 D、﹣34. 一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )A、m=3,n=5 B、m=n=4 C、m+n=4 D、m+n=85. 若二次函数y=ax2(a≠0)的图象过点(-2,-3),则必在该图象上的点还有( )A、(-3,-2) B、(2,3) C、(2,-3) D、(-2,3)6. 有一道题目:“在△ABC中,AB=AC , ∠A=40°,分别以B、C为圆心,以BC长为半径的两条弧相交于D点,求∠ABD的度数”. 保保的求解结果是∠ABD=10°.贝贝说:“保保考虑的不周全,∠ABD还应有另一个不同的值.”下列判断正确的是( )A、贝贝说得对,且∠ABD的另一个值是130° B、贝贝说的不对,∠ABD就得10° C、保保求的结果不对,∠ABD应得20° D、两人都不对,∠ABD应有3个不同值7. 若二次函数y=x2-6x+c的图象经过A(0,y1),B(4,y2)三点,则y1 , y2的大小关系正确的是( )A、y1>y2 B、y1=y2 C、y2>y1 D、y1≥y28. 如图,AB为⊙O的直径,C为AB上一点,AD∥OC , AD交⊙O于点D , 连接AC , CD , 设∠BOC=x°,∠ACD=y°,则下列结论成立的是( )
3. 二次函数y=(x﹣1)2﹣3的最小值是( )A、2 B、1 C、﹣2 D、﹣34. 一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )A、m=3,n=5 B、m=n=4 C、m+n=4 D、m+n=85. 若二次函数y=ax2(a≠0)的图象过点(-2,-3),则必在该图象上的点还有( )A、(-3,-2) B、(2,3) C、(2,-3) D、(-2,3)6. 有一道题目:“在△ABC中,AB=AC , ∠A=40°,分别以B、C为圆心,以BC长为半径的两条弧相交于D点,求∠ABD的度数”. 保保的求解结果是∠ABD=10°.贝贝说:“保保考虑的不周全,∠ABD还应有另一个不同的值.”下列判断正确的是( )A、贝贝说得对,且∠ABD的另一个值是130° B、贝贝说的不对,∠ABD就得10° C、保保求的结果不对,∠ABD应得20° D、两人都不对,∠ABD应有3个不同值7. 若二次函数y=x2-6x+c的图象经过A(0,y1),B(4,y2)三点,则y1 , y2的大小关系正确的是( )A、y1>y2 B、y1=y2 C、y2>y1 D、y1≥y28. 如图,AB为⊙O的直径,C为AB上一点,AD∥OC , AD交⊙O于点D , 连接AC , CD , 设∠BOC=x°,∠ACD=y°,则下列结论成立的是( ) A、x+y=90 B、2x+y=90 C、2x+y=180 D、x=y9. 二次函数y=x2+2x+c的图象与x轴的两个交点为A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m , n)是图象上一点,那么下列判断正确的是( )A、当n>0时,m<x1 B、当n>0时,m>x2 C、当n<0时,m<0 D、当n<0时,x1<m<x210. 如图,在△ABC中,AD是BC边上的高,⊙P是△ABC的外接圆,连结PA . 若AD=3,BD=1,BC=5,则PA的长( )
A、x+y=90 B、2x+y=90 C、2x+y=180 D、x=y9. 二次函数y=x2+2x+c的图象与x轴的两个交点为A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m , n)是图象上一点,那么下列判断正确的是( )A、当n>0时,m<x1 B、当n>0时,m>x2 C、当n<0时,m<0 D、当n<0时,x1<m<x210. 如图,在△ABC中,AD是BC边上的高,⊙P是△ABC的外接圆,连结PA . 若AD=3,BD=1,BC=5,则PA的长( ) A、2.5 B、 C、 D、2.8
A、2.5 B、 C、 D、2.8二、填空题:本大题有6个小题,每小题4分,共24分.
-
11. 一个不透明的袋中有若干个除颜色外完全相同的小球,其中黄球有6个.将袋中的球摇匀后,从中随机摸出一个球,记下它的颜色后再放回袋中,通过大量重复摸球试验后发现,摸到黄球的频率稳定在0.3左右,则袋中小球的个数为.12. 在二次函数y=ax2+bx+c(a≠0)中,y与x的部分对应值如表:
x
…
-1
0
1
2
3
…
y
…
0
2
m
n
0
…
则m,n的大小关系为mn.(填“>”“=”或“<”)
13. 如图,某博览会上有一圆形展示区,在其圆形边缘的点P处安装了一台监视器,它的监控角度是55°,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器 台. 14. 如图,有长为24m的篱笆,一边利用墙(墙长不限),则围成的花圃ABCD的面积最大为 m2 .
14. 如图,有长为24m的篱笆,一边利用墙(墙长不限),则围成的花圃ABCD的面积最大为 m2 . 15. 如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E . 若E是BD的中点,则AC的长是 .
15. 如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD交于点E . 若E是BD的中点,则AC的长是 . 16. 已知二次函数y=ax2-bx(a≠0),经过点P(m , 2).当y≥时,x的取值范围为x≤n-1或x≥-3-n . 则此函数的对称轴是;m的值可以是(写出一个即可).
16. 已知二次函数y=ax2-bx(a≠0),经过点P(m , 2).当y≥时,x的取值范围为x≤n-1或x≥-3-n . 则此函数的对称轴是;m的值可以是(写出一个即可).三、解答题:本大题有8个小题,共66分.解答应写文字说明、证明过程或演算步骤.
-
17. 如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点均在格点上.(1)、将△DEF绕点E逆时针旋转90°得到△D1EE1 , 画出△D1EF1 .(2)、若△DEF由△ABC绕着某点旋转得到的,则这点的坐标为 .18. 已知抛物线y=ax2+bx+3与x轴交于点A(-1,0)、B(3,0).(1)、求抛物线的解析式;(2)、过点D作x轴的平行线交抛物线于E、F两点,求EF的长.19. 一个不透明的布袋中装有3个只有颜色不同的球,其中1个黄球、2个红球.(1)、任意摸出1个球,记下颜色后不放回,再任意摸出1个球,求两次摸出的球恰好都是红球的概率(要求画树状图或列表);(2)、现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为 , 求n的值.20. 如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
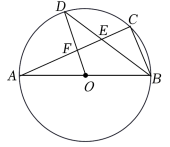 (1)、求证:点D为的中点;(2)、若DF=4,AC=16,求⊙O的直径.21. 如图,AB为⊙O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交⊙O于点E,连接CE.
(1)、求证:点D为的中点;(2)、若DF=4,AC=16,求⊙O的直径.21. 如图,AB为⊙O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交⊙O于点E,连接CE. (1)、求证∠A=∠D;(2)、若的度数为108° , 求∠E的度数.22. 已知二次函数y=x2+bx+c(b , c是常数)过点A(2、0),B(3n﹣4,y1),C(5n+6,y2)三点.(1)、若点A为此二次函数的顶点,求函数y的表达式.(2)、已知n<﹣5,
(1)、求证∠A=∠D;(2)、若的度数为108° , 求∠E的度数.22. 已知二次函数y=x2+bx+c(b , c是常数)过点A(2、0),B(3n﹣4,y1),C(5n+6,y2)三点.(1)、若点A为此二次函数的顶点,求函数y的表达式.(2)、已知n<﹣5,①若y1=y2 , 求b+c的取值范围;
②若c>0,试比较y1与y2的大小.
23. 如图1,AB为⊙O的直径,CD⊥AB于点E , , BF与CD交于点G . (1)、求证:CD=BF .(2)、若BE=1,BF=4,求GE的长.(3)、连结GO , OF , 如图2,求证: .24. 根据以下信息,探索完成任务.
(1)、求证:CD=BF .(2)、若BE=1,BF=4,求GE的长.(3)、连结GO , OF , 如图2,求证: .24. 根据以下信息,探索完成任务.如何设计种植方案?
素材1
某校为响应国家政策,在校内100平方米的土地上进行种植课实践,现有A、B,C三种作物的相关信息如表所示.已知5株A作物和2株B作物的产量共为7千克:10株A作物和6株B作物的产量共为15千克.
A作物
B作物
C作物
每平方米种植株树(株)
2
10
4
单株产量(千克)
x
y
1.6
素材2
由于A作物植株间距较大,可增加A作物每平方米的种植株树.经过实验发现,每平方米种植A作物每增加1株,A作物的单株产量减少0.1千克.而B,C单株产量不发生变化.
素材3
若同时种植A,B,C三种作物,实行分区域种植.
问题解决
任务1
确定单株产量
求x,y的值.
单一种植(全部种植A作物)
任务2
预估种植策略
要使A作物每平方米产量为4千克,则每平方米应种植多少株?
分区种植(种植A,B,C三种作物)
任务3
规划种植方案
设这100平方米的土地中有a平方米用于种植A作物,且每平方米的产量最大:有b平方米用于种植B作物,剩余的全用来种植C作物,a,b均为正整数.当这100平方米总产量为577千克时,求这三种作物的种植方案.