浙江省丽水市庆元二中2023-2024学年第一学期七年级数学第二次错题重做检测

试卷更新日期：2024-02-21 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30分。在每小题列出的选项中，选出符合题目的一项）

1. $\frac{1}{2022}$ 的相反数是（）

A、2022 B、 $- 2022$ C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 单项式 $- \frac{π x^{3} y^{2}}{5}$ 的系数与次数分别是（）

A、 $- \frac{π}{5} ， 5$ B、 $- \frac{π}{5} ， 4$ C、 $- \frac{1}{5} ， 6$ D、 $- \frac{1}{5} ， 5$

查看试题解析
3. 舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约 $499.5$ 亿千克，这个数用科学记数法应表示为（）

A、 $4.995 \times 10^{11}$ B、 $49.95 \times 10^{10}$ C、 $4.995 \times 10^{10}$ D、 $0.4995 \times 10^{11}$

查看试题解析
4. 已知代数式x＋2y的值是3，则代数式2x＋4y＋1的值是（）

A、1　 B、4　　 C、7　　 D、9

查看试题解析
5. 下列方程为一元一次方程的是（）

A、 $y + 3 = 0$ B、 $x + 2 y = 3$ C、 $1 + 1 = 2$ D、 $\frac{1}{y} + y = 2$

查看试题解析
6. 下列式子计算正确的个数有（）
$① a^{2} + a^{2} = a^{4}$ ； $② 3 x y^{2} - 2 x y^{2} = 1$ ； $③ 3 a b - 2 a b = a b$ ； $④ (- 2)^{3} - (- 3)^{2} = - 17$ ．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $0$ 个

查看试题解析
7. 实数a ， b ， c在数轴上的对应点的位置如图所示，若a与c互为相反数，则a ， b ， c中绝对值最大的数是（）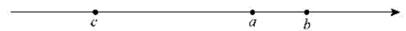

A、a B、b C、c D、无法确定

查看试题解析
8. 一轮船 $A$ 测得灯塔 $B$ 在其北偏西 $50 ゜$ 方向，灯塔 $C$ 在其南偏西 $40 ゜$ 方向，此时 $∠ B A C =$ （）

A、 $80 °$ B、 $90 °$ C、 $40 °$ D、不能确定

查看试题解析
9. $《$ 九章算术 $》$ 中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四．问人数，物价各几何？译文为：现有一些人共同买一个物品，每人出 $8$ 元，还盈余 $3$ 元；每人出 $7$ 元，则还差 $4$ 元，问共有多少人？这个物品的价格是多少？设这个物品的价格是 $x$ 元，则可列方程为
（）

A、 $8 x + 3 = 7 x + 4$ B、 $8 x - 3 = 7 x + 4$ C、 $\frac{x - 3}{8} = \frac{x + 4}{7}$ D、 $\frac{x + 3}{8} = \frac{x - 4}{7}$

查看试题解析
10. 下表中，填在各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（）

A、58 B、66 C、74 D、112

查看试题解析

二、填空题（本大题共6小题，共18分）

11. 比较大小： $- \frac{4}{7}$ $- \frac{5}{7} . ($ 填“ $<$ ”，“ $=$ ”或“ $>$ ” $)$

查看试题解析
12. 若 $12 a^{m - 1} b^{3}$ 与 $- \frac{1}{2} a^{3} b^{n}$ 是同类项，则mn= ．

查看试题解析
13. 若多项式 $8 x^{2} + (m + 1) x y - 5 y + x y - 8 (m$ 是常数 $)$ 中不含 $x y$ 项，则 $m$ 的值为．

查看试题解析
14. 如图， $O$ 是直线 $l$ 上一点， $∠ A O B = 100 °$ ，则 $∠ 1 + ∠ 2 =$ 度．

查看试题解析
15. 一个角的余角比它的补角的 $\frac{1}{3}$ 还少 $20 °$ ，则这个角的大小是．

查看试题解析
16. 按下面的程序计算：
如果输入 $x$ 的值是正整数，输出结果是 $214$ ，那么满足条件的 $x$ 的值可以是．

查看试题解析

三、解答题（本大题共8小题，共52分。解答应写出文字说明，证明过程或演算步骤）

17. 计算题：

(1)、 $7 - (- 4) + (- 5)$ ；

(2)、 $- \sqrt{16} + （ - 2 ）^{2} + \sqrt[3]{8}$

查看试题解析
18. 解方程：

(1)、 $4 x + 1 = 3 x - 5$

(2)、 $\frac{x + 1}{2} - 1 = \frac{2 - 3 x}{3}$

查看试题解析
19. 如图，已知正方形网格中的三点 $A$ ， $B$ ， $C$ ，按下列要求完成画图和解答：

(1)、画线段 $A B$ ，画射线 $A C$ ，画直线 $B C$ ；

(2)、取 $A B$ 的中点 $D$ ，并连接 $C D$ ；

(3)、根据图形可以看出： $∠$ 与 $∠$ 互为补角．

查看试题解析
20. 先化简，再求值： $\frac{1}{4} (- 4 a^{2} + 2 a - 8) - (a - 2)$ ，其中 $a = 2$ ．

查看试题解析
21. 已知点 $C$ 是线段 $A B$ 上一点， $A C = \frac{1}{3} A B$ .

(1)、若 $A B = 60$ ，求 $B C$ 的长；

(2)、若 $A B = a$ ， $D$ 是 $A C$ 的中点， $E$ 是 $B C$ 的中点，请用含 $a$ 的代数式表示 $D E$ 的长，并说明理由.

查看试题解析
22. 如图，直线 $A B$ 、 $C D$ 交于 $O$ 点，且 $∠ B O C = 80 °$ ， $O E$ 平分 $∠ B O C$ ， $O F$ 为 $O E$ 的反向延长线．

(1)、求 $∠ 2$ 和 $∠ 3$ 的度数；

(2)、 $O F$ 平分 $∠ A O D$ 吗？为什么？

查看试题解析
23. 如表是 $2022$ 年 $1$ 月日历，如图，用一长方形框在表中任意框 $4$ 个数．

(1)、若记长方形框左上角的一个数为 $x$ ，则另三个数用含 $x$ 的式子表示出来，从小到大依次是，，．

(2)、移动长方形框，被长方形框所框的 $4$ 个数之和可能是 $82$ 吗？请说明理由．

查看试题解析
24. 已知 $x = - 3$ 是关于 $x$ 的方程 $(k + 3) x + 2 = 3 x - 2 k$ 的解．

(1)、求 $k$ 的值；

(2)、在 $(1)$ 的条件下，已知线段 $A B = 6 c m$ ，点 $C$ 是线段 $A B$ 上一点，且 $B C = k A C$ ，若点 $D$ 是 $A C$ 的中点，求线段 $C D$ 的长．

(3)、在 $(2)$ 的条件下，已知点 $A$ 所表示的数为 $- 2$ ，点 $B$ 所表示的数为 $4$ ，有一动点 $P$ 从点 $A$ 开始以 $2$ 个单位长度每秒的速度沿数轴向左匀速运动，同时另一动点 $Q$ 从点 $B$ 开始以 $4$ 个单位长度每秒的速度沿数轴向左匀速运动，当时间为多少秒时，有 $P D = 2 Q D$ ？

查看试题解析