浙江省宁波市七校2023-2024学年八年级(上)培优数学试卷(12月份)
试卷更新日期:2024-02-21 类型:月考试卷
一、选择题:本题共6小题,每小题8分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 已知方程组的解满足 , 则取值范围是( )A、 B、 C、 D、2. 将一根长为的铅丝折成三段,再首尾相接围成一个三角形,如果要求围成的三角形边长都是整数,那么满足条件的三角形有( )A、个 B、个 C、个 D、个3. 如图,将一张三角形纸片的一角折叠,使点A落在外的处,折痕为.如果 , , , 那么下列式子中正确的是( )
 A、 B、 C、 D、4. 如图,是斜边上一点,且 , 为上任意一点,于点 , 于点 , 则的值是( )
A、 B、 C、 D、4. 如图,是斜边上一点,且 , 为上任意一点,于点 , 于点 , 则的值是( ) A、 B、 C、 D、5. 如图,在平面直角坐标系中, , , , 都是斜边在轴上,斜边长分别为 , , , 的等腰直角三角形,若的顶点坐标分别为 , , , 则依图中所示规律,的坐标为( )
A、 B、 C、 D、5. 如图,在平面直角坐标系中, , , , 都是斜边在轴上,斜边长分别为 , , , 的等腰直角三角形,若的顶点坐标分别为 , , , 则依图中所示规律,的坐标为( ) A、 B、 C、 D、6. 如图,为的高,点为的垂直平分线与的交点,点为上一点,若 , 且则的值为( )
A、 B、 C、 D、6. 如图,为的高,点为的垂直平分线与的交点,点为上一点,若 , 且则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题6分,共48分。
-
7. 如图,的度数为 .
 8. 如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为3和7,则△CDE的面积为.
8. 如图,点A在线段BG上,正方形ABCD和正方形DEFG的面积分别为3和7,则△CDE的面积为.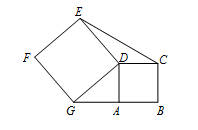 9. 如图,在中,为的中点,点为上一点,:: , 、交于点 , 若 , 则的面积为 .
9. 如图,在中,为的中点,点为上一点,:: , 、交于点 , 若 , 则的面积为 . 10. 如图,已知等腰 , , , 于点 , 点是延长线上一点,点是线段上一点, , 下面结论:
10. 如图,已知等腰 , , , 于点 , 点是延长线上一点,点是线段上一点, , 下面结论:
;
;
是等边三角形;
;
其中正确的有填上所有正确结论的序号 .11. 若不等式有解,则实数最小值是 .12. 如图,在中, , , 点是内一点,则点到三个顶点的距离和的最小值是 . 13. 如图,已知为等腰直角三角形, , , 为直线上的动点,则的最大值为 .
13. 如图,已知为等腰直角三角形, , , 为直线上的动点,则的最大值为 . 14. 甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为 , 两车间的距离与货车行驶时间之间的函数图象如图所示
14. 甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶,快递车到达乙地后,卸完物资并另装货物共用了分钟,然后按原路以另一速度返回,直至与货车相遇,已知货车行驶速度为 , 两车间的距离与货车行驶时间之间的函数图象如图所示
给出以下四个结论:
①快递车从甲地到乙地的速度是
②甲、乙两地之间的距离是
③图中点的坐标为
④快递车从乙地返回时的速度为
其中正确的是 填序号三、解答题:本题共5小题,共54分。解答应写出文字说明,证明过程或演算步骤。
-
15. 已知 , , 为三个非负数,且满足 , .(1)、求的取值范围;(2)、设 , 求的最大值和最小值.16. 在等腰和等腰中, , 连接 , 为中点,连接 .
 (1)、如图 , 请写出与的关系,并说明理由;(2)、将图中的旋转至图的位置,其他条件不变,中结论是否成立?请说明理由.17.
(1)、如图 , 请写出与的关系,并说明理由;(2)、将图中的旋转至图的位置,其他条件不变,中结论是否成立?请说明理由.17. (1)、如图所示,在中, , , , 求证 .(2)、如图所示,在中, , , 延长至使 , 求 .
(1)、如图所示,在中, , , , 求证 .(2)、如图所示,在中, , , 延长至使 , 求 .

