浙江省杭州市钱江区2023-2024学年九年级数学11月月考试卷

试卷更新日期：2024-02-21 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 一个不透明的袋子中装有2个红球、3个白球和4个黄球，每个球除颜色外都相同．从中任意摸出1个球，摸到红球的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{9}$ C、 $\frac{4}{9}$ D、 $\frac{1}{2}$

查看试题解析
2. 抛物线 $y = - (x - 2)^{2} + 1$ 的顶点坐标（）

A、 $(2 ， 1)$ B、 $(2 ， - 1)$ C、 $(- 2 ， 1)$ D、 $(- 2 ， - 1)$

查看试题解析
3. 若⊙O的半径为3cm，点A到圆心O的距离为2cm，则点A与⊙O的位置关系为（）

A、点A在圆外 B、点A在圆上 C、点A在圆内 D、不能确定

查看试题解析
4. 如图， $△ A B C$ 为钝角三角形，将 $△ A B C$ 绕点A按逆时针方向旋转 $12 0^{∘}$ 得到 $△ A B' C'$ ，连接 $B B'$ ，若 $A C' / / B B'$ ，则 $∠ C A B'$ 的度数为 $($ $)$

A、 $4 5^{∘}$ B、 $6 0^{∘}$ C、 $7 0^{∘}$ D、 $9 0^{∘}$

查看试题解析
5. 抛物线y＝x²向左平移5个单位，再向下平移3个单位后，所得的抛物线表达式是（）

A、y＝（x﹣5）²﹣3 B、y＝（x﹣5）²+3 C、y＝（x+5）²﹣3 D、y＝（x+5）²+3

查看试题解析
6. 点 $P$ 是 $⊙ O$ 内一点，过点 $P$ 的最长弦的长为10，最短弦的长为6，则 $O P$ 的长为（）

A、8 B、2 C、5 D、4

查看试题解析
7. 已知 $⊙ O$ 的半径为5，弦 $M N / / E F ，$ 且MN=6，EF=8，则弦MN和EF之间的距离为（）

A、7或1 B、7 C、1 D、7或3

查看试题解析
8. 已知点（3，y₁），（﹣2，y₂），（0，y₃）在抛物线y＝x²﹣2x+c上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₃＜y₂ B、y₃＜y₁＜y₂ C、y₁＜y₂＜y₃ D、y₂＜y₃＜y

查看试题解析
9. 如图，⊙O的半径为10，弦AB＝16，点M是弦AB上的动点且点M不与点A、B重合，若OM的长为整数，则这样的点M有几个？（）

A、4 B、5 C、7 D、9

查看试题解析
10. 已知二次函数y= $a$ x²+bx+c（ $a$ ≠0）的部分图象如图所示，对称轴为 $x = \frac{3}{2}$ ，且经过点（-1，0）．下列结论：①3 $a$ +b=0；②若点 $(\frac{1}{2} ， y_{1})$ ，（3，y₂）是抛物线上的两点，则y₁<y₂；③10b-3c=0；④若y≤c，则0≤x≤3．其中正确的有（）

A、1个 B、2 C、3个 D、4个

查看试题解析

二、填空题（每小题4分，共24分）

11. 扔一枚质地均匀的骰子，朝上的数字不大于4的概率是．

查看试题解析
12. 如图，校运动会铅球比赛时，小明投铅球行进过程中形成的抛物线．按照图中所示的平面直角坐标系，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则铅球推出的水平距离OA的长是m．

查看试题解析
13. 抛物线y=x²﹣8x+1的顶点坐标是．

查看试题解析
14. 如图，点A，B，C在 $⊙ O$ 上，且 $∠ B A C = 25 °$ ，则 $∠ O C B$ 的度数是

查看试题解析
15. 在平面直角坐标系xOy中，将二次函数y＝ax²－4ax＋c(a为常数，且a＜0)的图象沿着y轴向下平移，交x轴于O，A两点，则OA的长为．

查看试题解析
16. 如图，正方形 $A B C D$ 边长为2，点 $G$ 是以 $A B$ 为直径的半圆上的一个动点，点 $F$ 是边 $C D$ 上的一个动点，点 $E$ 是 $A D$ 的中点，则 $E F + F G$ 的最小值为．

查看试题解析

三、解答题（本大题8小题，共66分）

17. 随着互联网经济的发展，人们的购物模式发生了改变，不带现金也能完成支付，比如使用微信、支付宝、银行卡等．在一次购物中小明和小亮都想从微信（记为A）、支付宝（记为B）、银行卡（记为C）三种支付方式中选择一种方式进行支付．请用画树状图或列表的方法，求出两人恰好选择同一种支付方式的概率．

查看试题解析
18. 已知二次函数的图象经过（－6，0），（2，0），（0，－6）三点．

(1)、求这个二次函数的表达式；

(2)、求这个二次函数的顶点坐标．

查看试题解析
19. 今年“十一”假期期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中纪念奖；指向其余数字不中奖．

(1)、转动转盘中一等奖、二等奖、三等奖的概率是分别是多少？

(2)、顾客中奖的概率是多少？

(3)、“十一”这天有1800人参与这项活动，估计获得一等奖的人数是多少？

查看试题解析
20. 如图，AD、BC是⊙O的两条弦，且AB＝CD，求证：AD＝BC．

查看试题解析
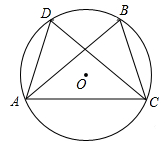21. 如图，点A ， B ， C在⊙O上，顺次连结AB ， BC ， CA ，且 $\overset{⏜}{ACB} = 210°$ ， $\overset{⏜}{AC} = 150°$ ．

(1)、求∠BAC的度数；

(2)、若⊙O的半径为3，求△ABC的面积．

查看试题解析
22. 某超市采购了两批同样的亚残会吉祥物飞飞挂件，第一批花了6600元，第二批花了8000元，第一批每个挂件的进价是第二批的1.1倍，且第二批比第一批多购进50个．

(1)、求第二批每个挂件的进价；

(2)、两批挂件售完后，该超市以第二批每个挂件的进价又采购一批同样的挂件，经市场调查发现，当售价为每个60元时，每周能卖出40个，若每降价1元，每周多卖10个，由于货源紧缺，每周最多能卖90个，求每个挂件售价定为多少元时，每周可获得最大利润，最大利润是多少？

查看试题解析
23. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C$ 、 $D$ 都在 $⊙ O$ 上，且 $C D$ 平分 $∠ A C B$ ，交 $A B$ 于点 $E$ .

(1)、求证： $∠ A B D = ∠ B C D$ ；

(2)、若 $D E = 13$ ， $A E = 17$ ，求 $⊙ O$ 的半径；

(3)、 $D F ⊥ A C$ 于点 $F$ ，试探究线段 $A F$ 、 $D F$ 、 $B C$ 之间的数量关系，并说明理由.

查看试题解析
24. 已知关于 $x$ 的函数 $y = a x^{2} + b x + c$ .

(1)、若 $a = 1$ ，函数的图象经过点 $(1 ， - 4)$ 和点 $(2 ， 1)$ ，求该函数的表达式和最小值；

(2)、若 $a = 1$ ， $b = - 2$ ， $c = m + 1$ 时，函数的图象与 $x$ 轴有交点，求 $m$ 的取值范围.

(3)、阅读下面材料：
设 $a > 0$ ，函数图象与 $x$ 轴有两个不同的交点 $A$ ， $B$ ，若 $A$ ， $B$ 两点均在原点左侧，探究系数 $a$ ， $b$ ， $c$ 应满足的条件，根据函数图象，思考以下三个方面：

①因为函数的图象与 $x$ 轴有两个不同的交点，所以 $Δ = b^{2} - 4 a c > 0$ ；

②因为 $A$ ， $B$ 两点在原点左侧，所以 $x = 0$ 对应图象上的点在 $x$ 轴上方，即 $c > 0$ ；

③上述两个条件还不能确保 $A$ ， $B$ 两点均在原点左侧，我们可以通过抛物线的对称轴位置来进一步限制抛物线的位置：即需 $- \frac{b}{2 a} < 0$ .

综上所述，系数 $a$ ， $b$ ， $c$ 应满足的条件可归纳为： ${\begin{array}{l} a > 0 \\ Δ = b^{2} - 4 a c > 0 \\ c > 0 \\ - \frac{b}{2 a} < 0 \end{array}$

请根据上面阅读材料，类比解决下面问题：

若函数 $y = a x^{2} - 2 x + 3$ 的图象在直线 $x = 1$ 的右侧与 $x$ 轴有且只有一个交点，求 $a$ 的取值范围.

查看试题解析