广东省茂名市信宜市2023-2024学年九年级上学期期末数学试题

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，是从上面看一个几何体得到的图形，则该几何体可能是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程3x²+2x+1＝0的二次项系数是（）

A、3 B、2 C、1 D、0

查看试题解析
3. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b$ ， $A B = c$ ，则 $c o s A$ 的值是（）

A、 $\frac{a}{c}$ B、 $\frac{b}{c}$ C、 $\frac{a}{b}$ D、 $\frac{b}{a}$

查看试题解析
4. 两个相似三角形的相似比是 $1 ： 2$ ．则其面积之比是（）

A、 $1 ： 1$ B、 $1 ： 2$ C、 $1 ： 3$ D、 $1 ： 4$

查看试题解析
5. 已知 $x = 1$ 是方程 $x^{2} + x - c = 0$ 的一个根，则 $c$ 的值是（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
6. 在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在 $0.3$ 左右，则布袋中黄球可能有（）

A、40个 B、35个 C、25个 D、15个

查看试题解析
7. 菱形不具有的性质是（）

A、对角相等 B、对边平行 C、对角线互相垂直 D、对角线相等

查看试题解析
8. 如图，双曲线 $y = \frac{k}{x}$ 与直线 $y = 2 x$ 相交于A、B两点，点A坐标为 $(1 ， 2)$ ，则点B坐标为（）

A、 $(- 1 ， - 2)$ B、 $(1 ， 2)$ C、 $(- 1 ， 2)$ D、 $(1 ， - 2)$

查看试题解析
9. 某商场销售一批衬衣，已知平均每天售出 $20$ 件衬衣时，每件盈利 $40$ 元，而且每件衬衣降价 $10$ 元时，平均每天可多售出 $20$ 件．如果商场平均每天要盈利 $1200$ 元，那么每件衬衣应降价多少元？若设每件衬衣降价x元，则可列方程为（）

A、 $(40 - x) (20 + 2 x) = 1200$ B、 $(40 + x) (20 + 2 x) = 1200$ C、 $(40 - x) (20 - 2 x) = 1200$ D、 $(40 + x) (20 - 2 x) = 1200$

查看试题解析
10. 如图，菱形ABCD的面积为24，对角线AG与BD交于点O，E是BC边的中点， $E F ⊥ B D$ 于点F， $E G ⊥ A C$ 于点G，则四边形EFOG的面积为（）

A、3 B、5 C、6 D、8

查看试题解析

二、填空题

11. 计算：tan45°=.

查看试题解析
12. 如图，日晷是我国古代利用日影测定时刻的仪器，晷针在晷面上所形成的投影属于投影．

查看试题解析
13. 如图，在△ABC中，D为边AC上的点，连接BD ，添加一个条件：，可以使得△ADB∽△ABC ．（只需写出一个）

查看试题解析
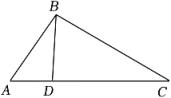14. 如图，在矩形ABCD中，对角线AC，BD相交于点O，若OA＝2，则BD的长为．

查看试题解析
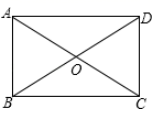15. 根据下面的表格请你写出方程 $a x^{2} + b x + c = 0$ （ $a \neq 0 ， a ， b ， c$ 为常数）的一个近似解：．（精确到0.1）
$x$
2
2.5
2.6
2.65
2.7
3
$a x^{2} + b x + c$
$- 1$
$- 0.25$
$- 0.04$
0.0725
0.19
1

查看试题解析

三、解答题

16. 解下列方程：

(1)、 $x (x - 1) = 0$ ；

(2)、 $x^{2} + 2 x - 3 = 0$ ．

查看试题解析
17. 试确定图中路灯的位置，并画出此时小明在路灯下的影子．

查看试题解析
18. 某景区检票口有A，B，C共3个检票通道，甲，乙两人到该景区游玩，两人分别从3个检票通道中随机选择一个检票.

(1)、甲选择A检票通道的概率是；

(2)、求甲，乙两人选择的检票通道恰好相同的概率.

查看试题解析
19. 如图，有一斜坡 $A B$ 长 $40 m$ ，坡顶离地面的高度为 $20 m$ ，求 $A C$ 的长度及此斜坡的倾斜角 $∠ A$ 的度数．

查看试题解析
20. 某公司前年盈利200万元，若该公司今年与去年的年增长率相同，则今年可盈利242万．

(1)、求这两年中平均每年增长的百分率；

(2)、若该公司盈利的年增长率继续保持不变，预计明年可盈利多少万元？

查看试题解析
21. 如图，四边形 $A B C D$ 是正方形， $△ B C E$ 是等边三角形，连接 $A E 、 D E$ ．

(1)、求证： $A E = D E$ ；

(2)、求 $∠ A E D$ 的度数．

查看试题解析
22. 如图，反比例函数 $y ＝ \frac{k}{x}$ 的图象与一次函数 $y ＝ x ＋ b$ 的图象交于点 $A (1 ， 4)$ 、点 $B (- 4 ， n)$ ．

(1)、求一次函数和反比例函数的解析式；

(2)、求 $△ O A B$ 的面积；

(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围．

查看试题解析
23. 综合与实践

(1)、探究发现：如图1，在 $4 \times 3$ 的网格图中，在线段 $A B$ 上求一点 $P$ ，使得 $B P = \frac{1}{2} A P$ ；小明同学发现，先在点 $B$ 的左侧取点 $C$ ，使 $B C$ 为1个单位长度，在点 $A$ 的右侧取点 $D$ ，使 $A D$ 为2个单位长度，然后连接 $C D$ 交 $A B$ 于点 $P$ （如图1），就可以得到点 $P$ 了．请你验证小明的做法，并求出 $t a n ∠ A P C$ 的值．

(2)、请你在图2中求作一点 $P$ ，使得 $B P = \frac{2}{3} A P$ ．

查看试题解析
24. 过四边形 $A B C D$ 的顶点A作射线 $A M$ ， P为射线 $A M$ 上一点，连接 $D P$ ．将 $A P$ 绕点A顺时针方向旋转至 $A Q$ ，记旋转角 $∠ P A Q = α$ ，连接 $B Q$ ．

(1)、如图1，数学兴趣小组探究发现，如果四边形 $A B C D$ 是正方形，且 $α = 90 °$ ．无论点P在何处，总有 $B Q = D P$ ，请证明这个结论．

(2)、如图2，如果四边形 $A B C D$ 是菱形， $∠ D A B = α = 60 °$ ， $∠ M A D = 15 °$ ，连接 $P Q$ ．当 $P Q ⊥ B Q$ ， $A B = \sqrt{6} + \sqrt{2}$ 时，求 $A P$ 的长；

(3)、如图3，如果四边形 $A B C D$ 是矩形， $A D = 6$ ， $A B = 8$ ， $A M$ 平分 $∠ D A C$ ， $α = 90 °$ ．在射线 $A Q$ 上截取 $A R$ ，使得 $A R = \frac{4}{3} A P$ ．当 $△ P B R$ 是直角三角形时，请直接写出 $A P$ 的长．

查看试题解析

$x$	2	2.5	2.6	2.65	2.7	3
$a x^{2} + b x + c$	$- 1$	$- 0.25$	$- 0.04$	0.0725	0.19	1