广东省湛江市赤坎区2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,共30分)
-
1. 下列交通标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列成语所描述的事件中是不可能事件的是( )A、守株待兔 B、水中捞月 C、水到渠成 D、不期而遇3. 的直径为10,圆心到直线的距离为3,下列位置关系正确( )A、
2. 下列成语所描述的事件中是不可能事件的是( )A、守株待兔 B、水中捞月 C、水到渠成 D、不期而遇3. 的直径为10,圆心到直线的距离为3,下列位置关系正确( )A、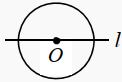 B、
B、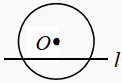 C、
C、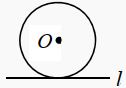 D、
D、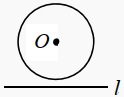 4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 正六边形的周长为6,则它的面积为( )A、 B、 C、 D、6. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、7. 小明热爱研究鸟类,每年定期去北京各个湿地公园观鸟.从他的观鸟记录年度总结中摘取部分数据如下:设小明从2020年到2022年观测鸟类种类数量的年平均增长率为 , 则下列方程正确的是( )
4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定5. 正六边形的周长为6,则它的面积为( )A、 B、 C、 D、6. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、7. 小明热爱研究鸟类,每年定期去北京各个湿地公园观鸟.从他的观鸟记录年度总结中摘取部分数据如下:设小明从2020年到2022年观测鸟类种类数量的年平均增长率为 , 则下列方程正确的是( )观鸟记录年度总结
2020年:观测鸟类150种
2021年:观测鸟类
2022年:观测鸟类216种
A、 B、 C、 D、8. 一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π9. , , , 是抛物线上的三点,则 , , 的大小关系是( )A、 B、 C、 D、10. 空地上有一段长为米的旧墙 , 工人师傅欲利用旧墙和木棚栏围成一个封闭的长方形菜园(如图),已知木棚栏总长为40米,所围成的长方形菜园面积为平方米.若 , , 则( ) A、有一种围法 B、有两种围法 C、不能围成菜园 D、无法确定有几种围法
A、有一种围法 B、有两种围法 C、不能围成菜园 D、无法确定有几种围法二、填空题(本大题共5小题,共15分)
-
11. 若是方程的一个根,则 .12. 如图,的半径为2,是函数的图象,是函数的图象,则阴影部分的面积是 .
 13. 如图,点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 . 小明发现线段与线段存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 .
13. 如图,点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 . 小明发现线段与线段存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是 . 14. 如图,在平面直角坐标系中,点在轴负半轴上,点在轴正半轴上,经过 , , , 四点, , , 则圆心点的坐标是.
14. 如图,在平面直角坐标系中,点在轴负半轴上,点在轴正半轴上,经过 , , , 四点, , , 则圆心点的坐标是.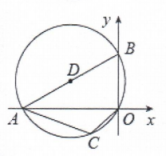 15. 如图,函数经过点 , 对称轴为直线:①;②;③;④;⑤若点、在抛物线上,则;⑥(为任意实数),其中结论正确的有 .
15. 如图,函数经过点 , 对称轴为直线:①;②;③;④;⑤若点、在抛物线上,则;⑥(为任意实数),其中结论正确的有 .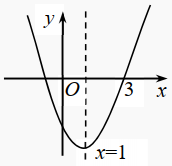
三、解答题(本大题共8小题,共75分.解答应写出文字说明,证明过程或演算步骤)
-
16. 用适当的方法解下列一元二次方程: .17. 无色酚酞溶液是一种常用酸碱指示剂,广泛应用于检验溶液酸碱性,通常情况下酚酞溶液遇酸性溶液不变色,遇中性溶液也不变色,遇碱性溶液变红色.现有5瓶缺失标签的无色液体:蒸馏水(中性)、白醋溶液(酸性)、食用纯碱溶液(碱性)、柠檬水溶液(酸性)、烧碱溶液(碱性).(1)、小丽同学从这5瓶溶液中随机取一瓶,取样,滴加酚酞溶液,且操作正确,则滴入酚酞溶液后呈现红色的概率为;(2)、小明从上述5瓶溶液中随机取两瓶,取样,滴加酚酞溶液,且操作正确,请你用列表或画树状图的方法,求选取的两瓶溶液滴入酚酞后都呈现红色的概率.18. 在如图所示的方格纸(1格长为一个单位长度)中,的三个顶点坐标分别为 , , .
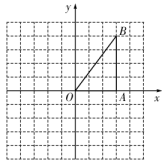 (1)、将绕点O顺时针旋转 , 画出旋转后的;(2)、在(1)的条件下,求点B绕点O旋转到点所经过的路径长(结果保留).19. 小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.
(1)、将绕点O顺时针旋转 , 画出旋转后的;(2)、在(1)的条件下,求点B绕点O旋转到点所经过的路径长(结果保留).19. 小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.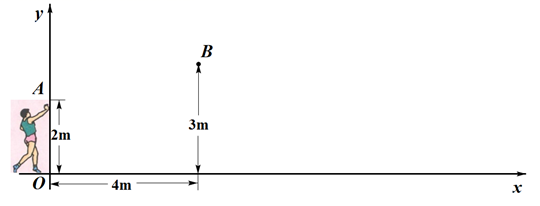 (1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.20. 如图,是的直径,是的一条弦,连接
(1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.20. 如图,是的直径,是的一条弦,连接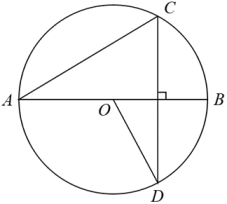 (1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.21. 请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量千克与每平方米种植的株数( , 且为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求关于的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?
(1)、求证:(2)、连接 , 过点作交的延长线于点 , 延长交于点 , 若为的中点,求证:直线为的切线.21. 请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量千克与每平方米种植的株数( , 且为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.(1)、求关于的函数表达式.(2)、每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?
