广东省茂名市高州市2023-2024学年九年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 在实数 , 0,1,中,最小的数是( )A、 B、0 C、1 D、2. 以下燕尾槽的主视图为( )
 A、
A、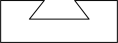 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、4. “中国天眼”是目前世界上唯一能观测深空的射电望远镜,其中心位置是一个正五边形,这个正五边形的内角和是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、7. 如图,两地被池塘隔开,小明先在外选一点 , 然后测出的中点 . 若的长为18米,则间的距离是( )
3. 在平面直角坐标系中,点关于x轴的对称点的坐标是( )A、 B、 C、 D、4. “中国天眼”是目前世界上唯一能观测深空的射电望远镜,其中心位置是一个正五边形,这个正五边形的内角和是( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 式子在实数范围内有意义,则的取值范围是( )A、 B、 C、 D、7. 如图,两地被池塘隔开,小明先在外选一点 , 然后测出的中点 . 若的长为18米,则间的距离是( )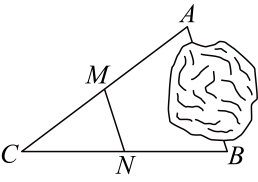 A、9米 B、18米 C、27米 D、36米8. 不等式组的解集在数轴上表示正确的是( )A、
A、9米 B、18米 C、27米 D、36米8. 不等式组的解集在数轴上表示正确的是( )A、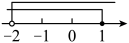 B、
B、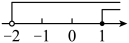 C、
C、 D、
D、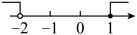 9. 将直线向上平移3个单位长度,得到的直线的解析式是( )A、 B、 C、 D、10. 如图,在正方形中,为的中点,为上一点(不与 , 重合),将沿所在的直线折叠,得到 , 连接 . 当时,的值是( )
9. 将直线向上平移3个单位长度,得到的直线的解析式是( )A、 B、 C、 D、10. 如图,在正方形中,为的中点,为上一点(不与 , 重合),将沿所在的直线折叠,得到 , 连接 . 当时,的值是( )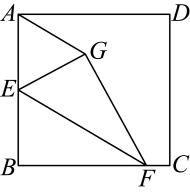 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
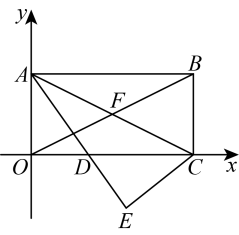
11. 因式分解: .12. 请写出一个与是同类项的式子: .13. 若 , 则 .14. 若 , 则的值为 .15. 如图,矩形对角线相交于点 , 沿着对角线折叠,使得点落在点处,其中点的坐标为长度为 , 则的纵坐标为 .
三、解答题(一):本大题共4小题,共28分.
-
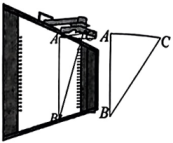
16.(1)、计算:(2)、用公式法解方程:17. 先化简,再求值: , 其中 .18. 教室里的投影仪投影时,可以把投影光线CA,CB及在黑板上的投影图像高度AB抽象成如图所示的△ABC, . 黑板上投影图像的高度 , CB与AB的夹角 , 求AC的长.(结果精确到1cm.参考数据: , , )
 19. 如图,的顶点在直线上,已知 , .
19. 如图,的顶点在直线上,已知 , .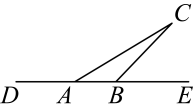 (1)、实践与操作:用尺规作图法作关于直线的对称图形;(2)、应用与计算:在(1)的条件下,若 , 求的长.
(1)、实践与操作:用尺规作图法作关于直线的对称图形;(2)、应用与计算:在(1)的条件下,若 , 求的长.四、解答题(二):本大题共3小题,每小题9分,共27分.
-
20. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.
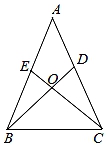 (1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 生物学上通常用“标记重捕法”来估算特定区域内某种群的数量.如在固定区域内用捕虫网捕捉了40只田鼠,将它们标记后放回直到充分混合后,用同一个捕虫网捕捉了80只田鼠,其中有16只是被标记的,于是估算该区域田鼠的数量为:
(1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.21. 生物学上通常用“标记重捕法”来估算特定区域内某种群的数量.如在固定区域内用捕虫网捕捉了40只田鼠,将它们标记后放回直到充分混合后,用同一个捕虫网捕捉了80只田鼠,其中有16只是被标记的,于是估算该区域田鼠的数量为:(只).
某研究小组考察了一湖泊中的某鱼种群的年龄组成,结果如下表,请回答问题:
年龄
A
B
C
D
……
个体数量
92
187
x
y
……
注:表中“”表示鱼的年龄年,表示年龄年,表示年龄年,表示年龄为年.
(1)、年龄为 , , 的个体数量的平均数为125,年龄在 , , , 的个体数量的中位数是95,则 , (其中).(2)、若将年龄为的鱼全部标记后并放回湖泊,充分混合后,捕捉120条鱼,其中被标记鱼有12条,那么该湖泊里一共约有多少条鱼?(3)、现捕获A,B,C,D年龄段的鱼各一条,从中任抓两条,请用列表或画树状图求抓到的是和年龄的鱼的概率.22. 综合与实践【问题背景】“夏至”过后,越来越多的市民喜欢去海边游玩,小明同学发现沙滩上有很多的遮阳伞为游客带来一丝清凉,如图1是沙滩上的圆形遮阳伞支架张开的状态,为了了解遮阳伞下方的遮阴面积,小明进行了如下操作调研.
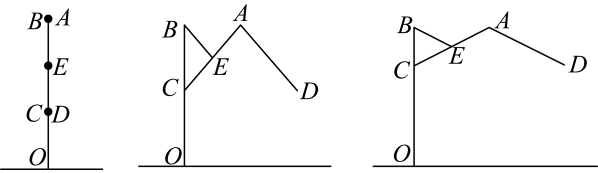
图1 图2 图3 图4
【测量与整理】通过操作发现,小明发现:如图2,当伞完全折叠时,伞顶与伞柄顶端点重合,两边主骨架的端点与重合;如图3,在撑开过程中,骨架的中点到点的距离始终等于的一半,;如图4,当伞完全张开时, .
【计算与分析】
(1)、当伞完全张开后,求的长度;(2)、当太阳光垂直照到遮阳伞上时,求伞完全张开时,遮挡住的阴影部分的面积.五、解答题(三):本大题共2小题,每小题10分,共20分.
-
23. 年世界环境日的主题是“减塑捡塑”,某城市为营造干净整洁的生活环境,加大垃圾分类的投入力度,准备购买两种型号的垃圾桶.市场调查反映:型垃圾桶每组的单价比型垃圾桶每组的单价多元,用元购买型垃圾桶的组数与用元购买型垃圾桶的组数相同.(1)、求两种型号垃圾桶每组的单价;(2)、该城市计划购买两种型号垃圾桶共组,且型垃圾桶的组数不少于型垃圾桶组数的 , 求购买这组垃圾桶所需的最大费用.24. 已知点在反比例函数的图象上,以为边长作正方形 , 使正方形顶点在轴上方,与轴的夹角为 .
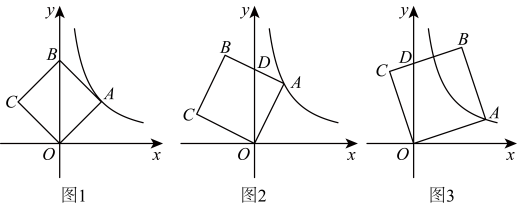 (1)、如图1,当点在轴上时,求点坐标;(2)、①如图2,当时,与轴相交于点 , 若 , 求点的坐标;
(1)、如图1,当点在轴上时,求点坐标;(2)、①如图2,当时,与轴相交于点 , 若 , 求点的坐标;②如图3,当时,与轴相交于点 , 若 , 求点的坐标.