浙江省杭州市上城区2023-2024学年上学期八年级期末数学试卷

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是是符合题目要求的．

1. 下列体育运动图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知三角形两边的长分别为2、4，第三边的长为整数，则第三边的长为（）

A、1 B、2 C、5 D、6

查看试题解析
3. 能说明命题“|a|＞0”是假命题的一个反例是（）

A、a＝﹣2 B、a＝0 C、a＝5 D、a＝π

查看试题解析
4. 如图，在△ABC和△ADE中，AC＝AE，AB＝AD，只添加一个条件，不能判定△ABC≌△ADE的是（）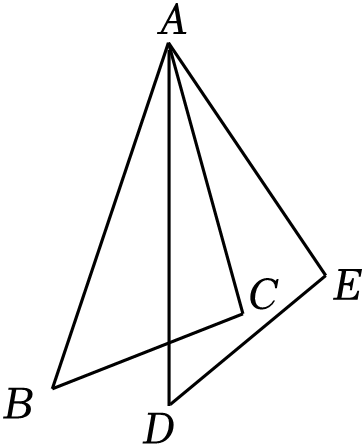

A、BC＝DE B、∠BAC＝∠DAE C、∠BAD＝∠CAE D、∠B＝∠D

查看试题解析
5. 已知点P（2，a）关于y轴的对称点为Q（b，﹣1），则ab的值为（）

A、2 B、﹣1 C、﹣2 D、﹣3

查看试题解析
6. 已知a＞b，下列不等式成立的是（）

A、﹣2a＜﹣2b B、a﹣2＜b﹣2 C、a+2＜b+2 D、3a＜3b

查看试题解析
7. 若实数a，b满足ab＞0，且a＞0，则函数y＝ax+b的图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 如图，DE和DF分别是线段AB和BC的垂直平分线，若∠A＝70°，∠C＝40°，则∠B的度数为（）

A、100° B、110° C、120° D、130°

查看试题解析
9. 已知（x₁ ， y₁），（x₂ ， y₂）为直线y＝﹣x+1上的两个点，且x₁＜x₂ ，则以下判断正确的是（）

A、若x₂＞0，则y₁＞0 B、若x₂＞0，则y₁＜0 C、若x₂＜0，则y₁＞0 D、若x₂＜0，则y₁＜0

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，首先沿着CD折叠，点B落在点E处，然后沿着FG折叠，使得点A与点E重合，则下列说法中（）
①EF⊥CE；②若BC＝3，AC＝4，那么 $F G = \frac{21}{40}$ ．

A、①正确，②正确 B、①正确，②错误 C、①错误，②正确 D、①错误，②错误

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

11. $x$ 的2倍与5的差是负数，用不等式表示为.

查看试题解析
12. 请写一个过（1，0）的一次函数表达式：．

查看试题解析
13. 平面直角坐标系中，已知点P（1，﹣3），则点P到x轴的距离是．

查看试题解析
14. 如图，在△ABC中，AB＝AC，∠A＝80°，CD是角平分线，DE∥BC，交AC于点E，则∠CDE＝°．

查看试题解析
15. 函数y₁＝x+1和y₂＝﹣x+b的交点落在第二象限，则b的取值范围为．

查看试题解析
16. 如图，在△ABC中，AB＝AC，AF⊥BC于F，BE⊥AC于E，且点D是AB的中点．

(1)、若△DEF的周长是8，则△ABC的周长是；

(2)、若AE：EC＝3：2，则AF：EF＝．

查看试题解析

三、解答题：本大题有7个小题，共66分。解答应写出文字说明、证明过程或演算步骤.

17. 解不等式组 ${\begin{array}{l} 3 - x > 2 x \\ \frac{x - 1}{2} ⩾ \frac{x}{3} - 1 \end{array}$ ，并把不等式组的解集在数轴上表示出来．

查看试题解析
18. 如图，AD＝AE，BD＝CE．

(1)、求证：∠B＝∠C；

(2)、若∠A＝40°，∠BEC＝70°，求∠C的度数．

查看试题解析
19. 如图，在平面直角坐标系中，已知点A（﹣5，2），B（﹣4，5），C（m，n）．

(1)、点C落在y轴正半轴，且到原点的距离为3，则m＝， n＝；

(2)、在平面坐标系中画出△ABC；

(3)、若△ABC边上任意一点P（x₀ ， y₀）平移后对应点P₁（x₀+4，y₀﹣1），在平面直角坐标系中画出平移后的△A₁B₁C₁ ．

查看试题解析
20. 燃油车和新能源车是人们在购车过程中的两个不同选择，方方调查了两款售价相同的燃油车和新能源车的相关数据．燃油车每千米的行驶费用为0.6元，若行驶距离均为600km，燃油车的花费比新能源车多300元．

(1)、求新能源车每千米的行驶费用；

(2)、若燃油车和新能源车每年的其它费用分别为6000元和9000元，问：每年行驶里程超过多少千米后，新能源车的年费用更低？（年费用＝年行驶费用+年其它费用）

查看试题解析
21. 在△ABC中，BD＝AB，AD＝CD，若∠C＝α，∠B＝β．

(1)、若α＝35°，求β的值；

(2)、求β关于α的函数表达式，并写出自变量α的取值范围；

(3)、判断点D能否为BC的中点，若能，求出α的值；若不能，请说明理由．

查看试题解析
22. 一次函数y₁＝kx+b（k≠0）恒过定点（3，2）．

(1)、若一次函数y₁＝kx+b还经过（0，5）点，求k的值；

(2)、一次函数y₁＝kx+b不经过第四象限，求k的取值范围；

(3)、另一函数y₂＝x﹣1，满足y₁﹣y₂＝b+1，且k≠1，求x的值．

查看试题解析
23. 【问题背景】如图①，在四边形ABCD中，∠A和∠C称为它的对角，若这个四边形满足：∠A+∠C＝180°，则这个四边形叫做为“对角互补四边形”．
【问题解决】

(1)、若四边形ABCD是“对角互补四边形”，且∠B＝3∠D，求∠B的度数；

(2)、如图②，∠MON＝60°，OB平分∠MON，A是射线ON上一动点，C是射线OM上的动点，且四边形COAB是“对角互补四边形”．
①若△COB是等腰三角形，求∠BAN的度数；
②若OB＝m，若S_△BOC：S_△BOA＝n，求OC的长（用含m、n的代数式表示）．

查看试题解析