浙江省宁波七中教育集团2023-2024学年第一学期八年级数学期末试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的。)
-
1. 下列图形是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 若a<b,c≠0,则下列不等式不一定成立的是( )A、 B、 C、 D、3. 我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图, , 则的依据是( )
2. 若a<b,c≠0,则下列不等式不一定成立的是( )A、 B、 C、 D、3. 我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图, , 则的依据是( ) A、SAS B、ASA C、AAS D、SSS4. 下列命题的逆命题是假命题的是( )A、等腰三角形的两个底角相等 B、全等三角形的对应边都相等 C、两直线平行,同旁内角互补 D、对顶角相等5. 关于一次函数y=3x-1的描述,下列说法正确的是( )A、图象经过第一、二、三象限 B、函数的图象与x轴的交点是 C、向下平移1个单位,可得到y=3x D、图象经过点6. 在平面直角坐标系中,点平移后能与原来的位置关于y轴对称,则应把点A( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位7. 适合的正整数a的所有值的平方和为( )A、13 B、14 C、5 D、168. 一次函数与正比例函数( k,b是常数,且)的图象可能是( )A、
A、SAS B、ASA C、AAS D、SSS4. 下列命题的逆命题是假命题的是( )A、等腰三角形的两个底角相等 B、全等三角形的对应边都相等 C、两直线平行,同旁内角互补 D、对顶角相等5. 关于一次函数y=3x-1的描述,下列说法正确的是( )A、图象经过第一、二、三象限 B、函数的图象与x轴的交点是 C、向下平移1个单位,可得到y=3x D、图象经过点6. 在平面直角坐标系中,点平移后能与原来的位置关于y轴对称,则应把点A( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位7. 适合的正整数a的所有值的平方和为( )A、13 B、14 C、5 D、168. 一次函数与正比例函数( k,b是常数,且)的图象可能是( )A、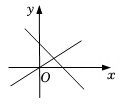 B、
B、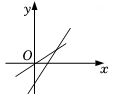 C、
C、 D、
D、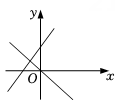 9. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=4,BF=2,△ADG的面积为 , 则点F到BC的距离为( )
9. 如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=4,BF=2,△ADG的面积为 , 则点F到BC的距离为( )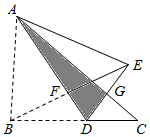 A、 B、 C、 D、10. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( )
A、 B、 C、 D、10. 如图,在中, , 点D为中点, , 绕点D旋转,分别与边 , 交于E,F两点,下列结论:①;②;③;④始终为等腰直角三角形,其中正确的是( ) A、①②④ B、①②③ C、③④ D、①②③④
A、①②④ B、①②③ C、③④ D、①②③④二、填空题(每小题3分,共18分)
-
11. 使二次根式有意义的的取值范围为 .12. 在平面直角坐标系中,若点在y轴上,则m的值是.13. 如图是折叠式沙发椅的示意图,若将度数调到图上所示度数为最舒适角度,求此时= .
 14. 若关于x的不等式组无解,a则的取值范围为 .15. 如图,直线交轴于点 , 以为直角边长作等腰 , 再过点作等腰交直线于点 , 再过点再作等腰交直线于点 , 以此类推,继续作等腰 , …, , 其中点…都在直线上,点…都在轴上,且 , , …都为直角.则点的坐标为 .
14. 若关于x的不等式组无解,a则的取值范围为 .15. 如图,直线交轴于点 , 以为直角边长作等腰 , 再过点作等腰交直线于点 , 再过点再作等腰交直线于点 , 以此类推,继续作等腰 , …, , 其中点…都在直线上,点…都在轴上,且 , , …都为直角.则点的坐标为 . 16. 在平面直角坐标系中 , , 过点B作直线lx轴,点是线l上的动点,以AP为边在AP右侧作等腰 , 使∠APQ=90°.
16. 在平面直角坐标系中 , , 过点B作直线lx轴,点是线l上的动点,以AP为边在AP右侧作等腰 , 使∠APQ=90°. (1)、当a=0时,则点Q的坐标是 .(2)、当点P在直线l上运动时,点Q也随之运动,则OQ的最小值是 .
(1)、当a=0时,则点Q的坐标是 .(2)、当点P在直线l上运动时,点Q也随之运动,则OQ的最小值是 .三、解答题(第17-19题各6分,第20-22题各8分,第23题10分,共52分)
-
17.(1)、解不等式组(2)、计算18. 如图,在等边的边上各取一点 , 使 , , 相交于点 .
 (1)、求证:;(2)、求的度数.19. 如图,在直角坐标系中,的三个顶点坐标分别为 , , , 请回答下列问题:
(1)、求证:;(2)、求的度数.19. 如图,在直角坐标系中,的三个顶点坐标分别为 , , , 请回答下列问题: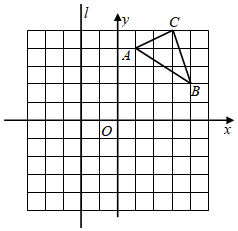 (1)、画出关于x轴的对称图形;直接写出A1、B1、C1的坐标;(2)、如图,在直线上找一点M,使得的值最小.(保留作图痕迹)20. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?21. 甲乙两人同时登山,甲、乙两人距离地面的高度y(米)与时间x(分)之间的函数图象如图所示.根据图象提供的信息,完成下列问题.
(1)、画出关于x轴的对称图形;直接写出A1、B1、C1的坐标;(2)、如图,在直线上找一点M,使得的值最小.(保留作图痕迹)20. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?21. 甲乙两人同时登山,甲、乙两人距离地面的高度y(米)与时间x(分)之间的函数图象如图所示.根据图象提供的信息,完成下列问题. (1)、求甲距离地面的高度米与时间分之间的函数关系式.(2)、当时,求乙距离地面的高度米与时间分之间的函数关系式.(3)、当为何值时,甲乙距离地面的高度相差20米.22. 定义:若是的三边,且 , 则称为“方倍三角形”.(1)、若是“方倍三角形”,且斜边AB= , 则该三角形的面积为 .(2)、如图,是“方倍三角形”,且 , 求证:为等边三角形.
(1)、求甲距离地面的高度米与时间分之间的函数关系式.(2)、当时,求乙距离地面的高度米与时间分之间的函数关系式.(3)、当为何值时,甲乙距离地面的高度相差20米.22. 定义:若是的三边,且 , 则称为“方倍三角形”.(1)、若是“方倍三角形”,且斜边AB= , 则该三角形的面积为 .(2)、如图,是“方倍三角形”,且 , 求证:为等边三角形. (3)、如图,中, , , 是边上一点,将沿进行折叠,点落在点处,连接 , , 若为“方倍三角形”,且 , 求的长.
(3)、如图,中, , , 是边上一点,将沿进行折叠,点落在点处,连接 , , 若为“方倍三角形”,且 , 求的长. 23. 如图1,点的坐标是 , 垂直于轴于点 , 是直线在第一象限上的动点,交轴于点 .
23. 如图1,点的坐标是 , 垂直于轴于点 , 是直线在第一象限上的动点,交轴于点 . (1)、求当点的坐标为时,
(1)、求当点的坐标为时,①求直线的解析式;
②求的面积;
③为坐标轴上一点,且是以为底边的等腰三角形,请直接写出点的坐标.
(2)、如图2,是线段上一点,且 , 取的中点 , 求的面积.四、附加题(第24题4分,第25题6分,共10分)
 的解集为 , 那么所有满足条件的a的值之和为 .
的解集为 , 那么所有满足条件的a的值之和为 . 