浙江省宁波市奉化区2023-2024学年八年级上学期数学期末文化素养测评

试卷更新日期：2024-02-21 类型：期末考试

进入出卷网下载

一、选择题（每小题5分，共35分）

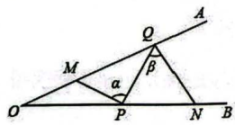
1. 已知一次函数 $y = - 3 x + m$ 图象上的三点 $P (n ， a)$ ， $Q (n - 1 ， b)$ ， $R (n + 2 ， c)$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $b > a > c$ B、 $c > b > a$ C、 $c > a > b$ D、 $a > b > c$

查看试题解析
2. 若关于 $x$ 的不等式 $2 x - a > 0$ 的解集中存在负数解，但不存在负整数解，则 $a$ 的取值范围是（）.

A、 $a \geq - 2$ B、 $a < 0$ C、 $- 2 \leq a < 0$ D、 $- 2 < a \leq 0$

查看试题解析
3. 在 $△ A B C$ 中， $∠ A B C = 30 °$ ， $A B$ 边长为4， $A C$ 边的长度可以，1、2、3、4、5中取值，满足这些条件的互不全等的三角形的个数是（）.

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 如图， $A B ⊥ C D$ 于点 $O$ ，点 $E$ 、 $F$ 分别是射线 $O A$ 、 $O C$ 上的动点（不与点 $O$ 重合），延长 $F E$ 至点 $G$ ， $∠ B O F$ 的角平分线及其反向延长线分别交 $∠ F E O$ 、 $∠ G E O$ 的角平分线于点 $M$ 、 $N$ .若 $△ M E N$ 中有一个角是另一个角的3倍，则 $∠ E F O$ 为（）.

A、 $45 °$ 或 $30 °$ B、 $30 °$ 或 $60 °$ C、 $45 °$ 或 $60 °$ D、 $67.5 °$ 或 $45 °$

查看试题解析
5. 如图，在平面直角坐标系中有一个 $3 \times 3$ 的正方形网格，其右下角格点（小正方形的顶点） $A$ 的坐标为 $(- 1 ， 1)$ ，左上角格点 $B$ 的坐标为 $(- 4 ， 4)$ ，若分布在直线 $y = - k x - k$ 两侧的格点数相同，则 $k$ 的取值可以是（）.

A、 $\frac{5}{2}$ B、 $\frac{7}{4}$ C、2 D、 $\frac{3}{2}$

查看试题解析
6. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ，分别以 $A B$ 、 $A C$ 、 $B C$ 为边在 $A B$ 的同侧作正方形 $A B E F$ 、 $A C P Q$ 、 $B C M N$ ，四块阴影部分的面积分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 、 $S_{4}$ .若已知 $A C \times B C = 12$ ，则 $S_{1} + S_{2} + S_{3} + S_{4}$ 的值为（）

A、18 B、24 C、25 D、36

查看试题解析
7. 设 $a \leq b \leq c$ 是三角形的三边长，且 $a$ ， $b$ ， $c$ 都是自然数，如果 $b = n$ ，则这样的三角形有（）

A、 $3 n - 2$ B、 $2 n - 1$ C、 $\frac{1}{2} n (n - 1)$ D、 $\frac{1}{2} n (n + 1)$

查看试题解析

二、填空题（每小题5分，共25分）

8. 在 $△ A B C$ 中， $E$ 为边 $A C$ 的中点，点 $D$ 在边 $B C$ 上， $B D ： C D = 5 ： 8$ ， $A D$ 、 $B E$ 交于点 $F$ ，若 $△ A B C$ 的面积为26，则 $S_{△ A E F} - S_{△ B D F} =$ .

查看试题解析
9. 如图， $∠ A O B = 20 °$ ，点 $M$ 、 $N$ 分别是边 $O A$ 、 $O B$ 上的定点，点 $P$ 、 $Q$ 分别是边 $O B$ 、 $O A$ 上的动点，记 $∠ M P Q = α$ ， $∠ P Q N = β$ ，当 $M P + P Q + Q N$ 最小时，则 $β - α$ 的值为.

查看试题解析
10. 如图，在平面直角坐标系中，一次函数 $y = 2 x - 2$ 的图象分别交 $x$ 、 $y$ 轴于点 $A$ 、 $B$ ，将直线 $A B$ 绕点 $B$ 按顺时针方向旋转 $45 °$ ，交 $x$ 轴于点 $C$ ，则直线 $B C$ 的函数表达式是.

查看试题解析
11. 若自然数 $x < y < z$ ， $n$ 为整数，且 $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = n$ ，则 $x + y - z =$ .

查看试题解析
12. 如图，等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 70 °$ ， $O$ 为 $△ A B C$ 内一点，且 $∠ O C B = 5 °$ ， $∠ A B O = 25 °$ ，则 $∠ O A C =$ .

查看试题解析

三、解答题（共40分）

13. 春节前夕，某商店从厂家购进 $A$ 、 $B$ 两种礼盒，已知 $A$ 、 $B$ 两种礼盒的单价比为 $3 ： 4$ ，单价和为210元，该商店购进这两种礼盒恰好用去9900元.

(1)、求 $A$ 、 $B$ 两种礼盒的单价分别是多少元？

(2)、若购进 $A$ 种礼盒最多36个， $B$ 种礼盒的数量不超过 $A$ 种礼盒数量的2倍，则有几种进货方案？

(3)、根据市场行情，销售一个 $A$ 种礼盒可获利12元，销售一个 $B$ 种礼盒可获利18元.为奉献爱心，该店主决定每售出一个 $B$ 种礼盒，为爱心公益基金捐款 $m$ 元，每个 $A$ 种礼盒的利润不变，要使礼盒全部售出后所有方案获利相同， $m$ 值是多少？此时店主获利多少元？

查看试题解析
14. 如果一个数能表示成 $2 x^{2} + 2 x y + y^{2}$ （ $x$ ， $y$ 是整数），我们称这个数为“好数”.

(1)、写出10，11，12，…，20中的“好数”.

(2)、如果 $m$ ， $n$ 都是“好数”，请分别判断 $m + n$ 和 $m n$ 一定是“好数”吗？如果不是，请举反例说明；如果是，请说明理由.

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ C > ∠ B$ ， $A D$ 平分 $∠ B A C$ ，点 $E$ 是 $B C$ 的中点，过点 $E$ 作 $E H ⊥ A D$ 交 $A D$ 延长线于点 $H$ .

(1)、求证： $∠ C - ∠ B = 2 ∠ D E H$ .

(2)、若 $A B = m$ ， $A C = n$ ， $∠ A C B - ∠ D E H = 60 °$ ，求 $E H$ 的长（用 $m$ 、 $n$ 的代数式表示）.

查看试题解析