广西壮族自治区柳州市2023-2024学年八年级上学期期末数学试题
试卷更新日期:2024-02-21 类型:期末考试
一、选择题(本题共10小题,每小题3分,满分30分。)
-
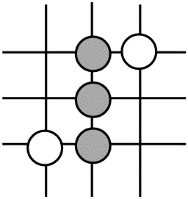
1. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑白棋子摆成的图案是中心对称图形的是( )A、
B、
B、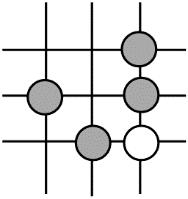
C、
C、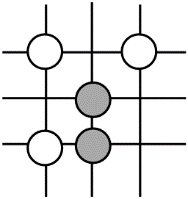
D、
D、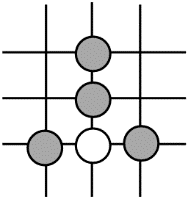
2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列长度的三条线段能首尾相接构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )A、 B、 C、 D、5. 如图,在中,画出边上的高( )A、
2. 下列运算中正确的是( )A、 B、 C、 D、3. 下列长度的三条线段能首尾相接构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 华为麒麟990芯片采用了最新的0.000000007米的工艺制程,数0.000000007用科学记数法表示为( )A、 B、 C、 D、5. 如图,在中,画出边上的高( )A、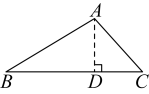 B、
B、 C、
C、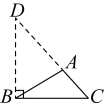 D、
D、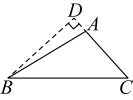 6. 若一个多边形的内角和比它的外角和大 , 则该多边形的边数为( )A、6 B、7 C、8 D、97. 若 、 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、8. 下列因式分解正确的是( )A、 B、 C、 D、9. 如图,在中, , , 平分 , 点E在上,把沿直线折叠,使点B落在点F处,连接 , 若 , 则的度数为( )
6. 若一个多边形的内角和比它的外角和大 , 则该多边形的边数为( )A、6 B、7 C、8 D、97. 若 、 的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、8. 下列因式分解正确的是( )A、 B、 C、 D、9. 如图,在中, , , 平分 , 点E在上,把沿直线折叠,使点B落在点F处,连接 , 若 , 则的度数为( ) A、 B、 C、 D、10. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如,利用图1可以得到 , 那么利用图2所得到的数学等式为( )
A、 B、 C、 D、10. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如,利用图1可以得到 , 那么利用图2所得到的数学等式为( )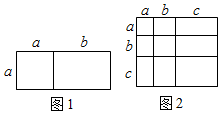 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6小题,满分18分,每小题3分)
-
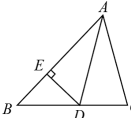
11. 若分式的值为0,则的值为 .12. 点关于轴对称的点的坐标为 .13. 如图,在中,平分若则 .
 14. 已知 , , 则代数式的值为 .15. 如图,中, , 以点B为圆心,的长为半径画弧交于点C,E,再分别以点C与点E为圆心,大于长的一半为半径画弧,两弧交于点F,连接交AC于点D,若 , 则是°.
14. 已知 , , 则代数式的值为 .15. 如图,中, , 以点B为圆心,的长为半径画弧交于点C,E,再分别以点C与点E为圆心,大于长的一半为半径画弧,两弧交于点F,连接交AC于点D,若 , 则是°.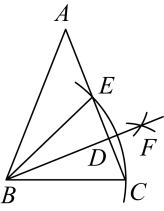 16. 如图,在等边中,于D,E是线段上一点,F是边上一点,且满足 , G是的中点,连接 , 则下列四个结论:①;②;③;④;⑤当时, , 其中正确的有.(填序号)
16. 如图,在等边中,于D,E是线段上一点,F是边上一点,且满足 , G是的中点,连接 , 则下列四个结论:①;②;③;④;⑤当时, , 其中正确的有.(填序号)
三、解答题(本题共7小题,满分52分,解答时应写出必要的文字说明、演算步骤或推理过程)
-
17. 分解因式: .18. 计算: .19. 解方程: .20. 如图,在平面直角坐标系中,已知 .
 (1)、作出关于直线l(直线l上各点的纵坐标都是1)对称的图形 , 并写出 , , 的坐标.( , );( , );( , ).(2)、在直线l上找一点P,使得的长度最小(只要作出图形即可);(3)、若中有一点 , 写出点Q在中对应点的坐标是( , ).21. 已知:如图,点在一条直线上,两点在直线的同侧, , , , 求证: .
(1)、作出关于直线l(直线l上各点的纵坐标都是1)对称的图形 , 并写出 , , 的坐标.( , );( , );( , ).(2)、在直线l上找一点P,使得的长度最小(只要作出图形即可);(3)、若中有一点 , 写出点Q在中对应点的坐标是( , ).21. 已知:如图,点在一条直线上,两点在直线的同侧, , , , 求证: . 22. 习总书记在党的第二十次全国代表大会上,报告指出:“积极稳妥推进碳达峰碳中和”某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车进价是每辆B型汽车进价的1.5倍,若用1500万元购进A型汽车的数量比1200万元购进B型汽车的数量少20辆.求每辆B型汽车进价是多少万元?23. 【综合与探究】新定义:连接三角形两边中点的线段叫做三角形的中位线.
22. 习总书记在党的第二十次全国代表大会上,报告指出:“积极稳妥推进碳达峰碳中和”某公司积极响应节能减排号召,决定采购新能源A型和B型两款汽车,已知每辆A型汽车进价是每辆B型汽车进价的1.5倍,若用1500万元购进A型汽车的数量比1200万元购进B型汽车的数量少20辆.求每辆B型汽车进价是多少万元?23. 【综合与探究】新定义:连接三角形两边中点的线段叫做三角形的中位线.性质:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
理解:如图①,在中,点D,E分别是的中点,那么为的一条中位线.可得且 .
应用:如图②,在中, , 点D,E分别在边 , 上,且 . 点M,N,P分别是 , 和的中点.已知 .
 (1)、当时,
(1)、当时,①请直接写出:与的数量关系 ▲ ; ▲ ;
②是否存在点D,使得以P,M,N为顶点的三角形与全等?若存在,请求出点D的位置;若不存在,请说明理由;
(2)、将绕点A旋转,当点D在内时(如图③),试说明与的数量关系,并求出的度数(用含α的式子表示).